Mała Delta
Nieskończoność
Zbiory duże
W poprzedniej części tej opowieści o nieskończonościach rozważaliśmy twierdzenie Cantora, które stanowi, że żaden zbiór 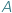 nie jest równoliczny ze zbiorem jego podzbiorów
nie jest równoliczny ze zbiorem jego podzbiorów 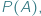 co symbolicznie notujemy
co symbolicznie notujemy 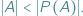 Szczególnie zajmowaliśmy się przypadkiem, gdy
Szczególnie zajmowaliśmy się przypadkiem, gdy 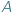 jest zbiorem liczb naturalnych
jest zbiorem liczb naturalnych 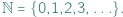
Studiowaliśmy także zbiór liczb całkowitych  oraz zbiór liczb wymiernych
oraz zbiór liczb wymiernych  pokazując, że każdy z nich jest równoliczny ze zbiorem liczb naturalnych. Takie zbiory nazywane są zbiorami przeliczalnymi. Inaczej mówiąc, są to zbiory, których elementy można zakwaterować w hotelu Hilberta. Chociaż są nieskończone, to z naszej perspektywy wydają się relatywnie "małe". Przynajmniej w porównaniu z innymi zbiorami, które rozważaliśmy. A były to: przedział
pokazując, że każdy z nich jest równoliczny ze zbiorem liczb naturalnych. Takie zbiory nazywane są zbiorami przeliczalnymi. Inaczej mówiąc, są to zbiory, których elementy można zakwaterować w hotelu Hilberta. Chociaż są nieskończone, to z naszej perspektywy wydają się relatywnie "małe". Przynajmniej w porównaniu z innymi zbiorami, które rozważaliśmy. A były to: przedział ![|[0,1],](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/3x-0a57d3e4a714a826d1d2e2e90cbe1e242dfb8b45-im-33,33,33-FF,FF,FF.gif) zbiór liczb rzeczywistych
zbiór liczb rzeczywistych  zbiór wszystkich nieskończonych ciągów zero-jedynkowych oraz zbiór wszystkich podzbiorów zbioru liczb naturalnych
zbiór wszystkich nieskończonych ciągów zero-jedynkowych oraz zbiór wszystkich podzbiorów zbioru liczb naturalnych 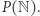 Wiemy, że żaden z nich nie jest równoliczny ze zbiorem liczb naturalnych. Są one ewidentnie "większe" - dla każdego ustawienia elementów dowolnego z tych zbiorów w pary z liczbami naturalnymi znajdowaliśmy element, który do żadnej pary nie trafił. Zauważyliśmy także, że zbiór wszystkich nieskończonych ciągów zero-jedynkowych oraz zbiór wszystkich podzbiorów zbioru liczb naturalnych
Wiemy, że żaden z nich nie jest równoliczny ze zbiorem liczb naturalnych. Są one ewidentnie "większe" - dla każdego ustawienia elementów dowolnego z tych zbiorów w pary z liczbami naturalnymi znajdowaliśmy element, który do żadnej pary nie trafił. Zauważyliśmy także, że zbiór wszystkich nieskończonych ciągów zero-jedynkowych oraz zbiór wszystkich podzbiorów zbioru liczb naturalnych 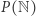 są równoliczne, ponieważ każdy podzbiór zbioru liczb naturalnych można ustawić w parę z ciągiem zer i jedynek, który go koduje. Wszystkie wymienione tu zbiory nazywa się zbiorami mocy continuum. Okazuje się bowiem, choć może być to z początku zaskakujące, że one też są parami równoliczne, czemu spróbujemy się teraz przyjrzeć dokładniej.
są równoliczne, ponieważ każdy podzbiór zbioru liczb naturalnych można ustawić w parę z ciągiem zer i jedynek, który go koduje. Wszystkie wymienione tu zbiory nazywa się zbiorami mocy continuum. Okazuje się bowiem, choć może być to z początku zaskakujące, że one też są parami równoliczne, czemu spróbujemy się teraz przyjrzeć dokładniej.
Jak zatem ustawić w pary elementy przedziału ![|[0, 1]](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/1x-3080d35a7d11616642b8722cf7a82642f2ad9a72-im-33,33,33-FF,FF,FF.gif) ze wszystkimi liczbami rzeczywistymi? Prościej będzie na początku rozważyć przypadek przedziału otwartego
ze wszystkimi liczbami rzeczywistymi? Prościej będzie na początku rozważyć przypadek przedziału otwartego 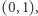 czyli przedziału wszystkich liczb większych od 0 i mniejszych od
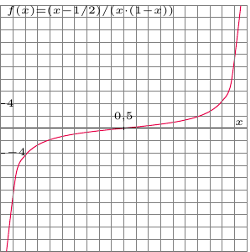
czyli przedziału wszystkich liczb większych od 0 i mniejszych od  Czytelnik, który miał do czynienia z funkcjami rzeczywistymi, znajdzie pewnie po chwili kilka sposobów takiego ustawienia liczb w pary. Na przykład, można liczbę
Czytelnik, który miał do czynienia z funkcjami rzeczywistymi, znajdzie pewnie po chwili kilka sposobów takiego ustawienia liczb w pary. Na przykład, można liczbę  z przedziału
z przedziału  ustawić w parę z liczbą rzeczywistą
ustawić w parę z liczbą rzeczywistą 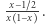 Rzeczywiście, dwóm różnym liczbom z przedziału
Rzeczywiście, dwóm różnym liczbom z przedziału  przyporządkujemy dwie różne liczby rzeczywiste i, co więcej, wszystkie liczby rzeczywiste zostaną wykorzystane, co doskonale ilustruje powyższy wykres funkcji
przyporządkujemy dwie różne liczby rzeczywiste i, co więcej, wszystkie liczby rzeczywiste zostaną wykorzystane, co doskonale ilustruje powyższy wykres funkcji 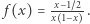
A zatem wiemy, że 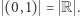 Musimy jeszcze wykazać, że
Musimy jeszcze wykazać, że ![| (0,1) = [0,1] .](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/2x-523c5aad7cd33fc1500a8ac2388ab496d18eb3e1-im-33,33,33-FF,FF,FF.gif) Inaczej mówiąc, musimy ustawić w odpowiednie pary wszystkie liczby tych dwóch przedziałów tak, żeby uwzględnić dwie "dodatkowe" liczby (0 i
Inaczej mówiąc, musimy ustawić w odpowiednie pary wszystkie liczby tych dwóch przedziałów tak, żeby uwzględnić dwie "dodatkowe" liczby (0 i  ) w jednym ze zbiorów. Zadanie to jest ładnym problemem kombinatorycznym, zachęcam więc Czytelnika do samodzielnego zastanowienia się nad nim przed analizą poniższego rozwiązania. Rozważmy pewien nieskończony ciąg liczb, na przykład
) w jednym ze zbiorów. Zadanie to jest ładnym problemem kombinatorycznym, zachęcam więc Czytelnika do samodzielnego zastanowienia się nad nim przed analizą poniższego rozwiązania. Rozważmy pewien nieskończony ciąg liczb, na przykład 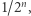 dla
dla 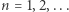 Teraz, jeśli liczba
Teraz, jeśli liczba 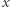 z przedziału
z przedziału 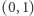 nie należy do tego ciągu, to ustawiam ją w parę z odpowiadającą jej tą samą liczbą
nie należy do tego ciągu, to ustawiam ją w parę z odpowiadającą jej tą samą liczbą 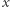 z przedziału
z przedziału ![|[0,1].](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/9x-523c5aad7cd33fc1500a8ac2388ab496d18eb3e1-im-33,33,33-FF,FF,FF.gif) Kolejne liczby z wyróżnionego ciągu przesuwam o dwa miejsca (podobnie jak przesuwaliśmy gości w hotelu Hilberta), tak żeby pierwsze dwa wyrazy tego ciągu mogły być towarzyszami w parach z 0 i
Kolejne liczby z wyróżnionego ciągu przesuwam o dwa miejsca (podobnie jak przesuwaliśmy gości w hotelu Hilberta), tak żeby pierwsze dwa wyrazy tego ciągu mogły być towarzyszami w parach z 0 i  To znaczy,
To znaczy, 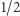 z przedziału
z przedziału  ustawiam w parę z 0 z przedziału
ustawiam w parę z 0 z przedziału ![[0,1],1/4](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/13x-523c5aad7cd33fc1500a8ac2388ab496d18eb3e1-im-33,33,33-FF,FF,FF.gif) - w parę z liczbą
- w parę z liczbą 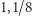 - w parę z
- w parę z 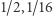 z
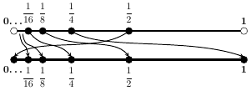
z  itd. (patrz rysunek). Czyli dla
itd. (patrz rysunek). Czyli dla 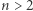 ustawiam
ustawiam 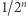 w parę z
w parę z  Rzeczywiście, ustawiłem wszystkie liczby z przedziału
Rzeczywiście, ustawiłem wszystkie liczby z przedziału  w pary z liczbami z przedziału
w pary z liczbami z przedziału ![|[0, 1],](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/21x-523c5aad7cd33fc1500a8ac2388ab496d18eb3e1-im-33,33,33-FF,FF,FF.gif) wykorzystując wszystkie liczby z obu przedziałów dokładnie raz. A zatem
wykorzystując wszystkie liczby z obu przedziałów dokładnie raz. A zatem ![[0,1] = (0,1) = R .](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/22x-523c5aad7cd33fc1500a8ac2388ab496d18eb3e1-im-33,33,33-FF,FF,FF.gif)
Najtrudniejsze zadanie jednak przed nami. Musimy jeszcze wykazać, że liczb z przedziału ![|[0, 1]](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/1x-b1d54eb865c560813fcbcbaa71824aa666b630f0-im-33,33,33-FF,FF,FF.gif) jest tyle samo, co nieskończonych ciągów zero-jedynkowych. Rozbijmy ten ostatni zbiór na dwie części: niech
jest tyle samo, co nieskończonych ciągów zero-jedynkowych. Rozbijmy ten ostatni zbiór na dwie części: niech 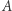 będzie zbiorem tych nieskończonych ciągów zero-jedynkowych, które od pewnego miejsca mają już tylko jedynki, zaś
będzie zbiorem tych nieskończonych ciągów zero-jedynkowych, które od pewnego miejsca mają już tylko jedynki, zaś 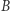 niech będzie zbiorem wszystkich pozostałych ciągów. Zatem zbiór wszystkich nieskończonych ciągów zero-jedynkowych to
niech będzie zbiorem wszystkich pozostałych ciągów. Zatem zbiór wszystkich nieskończonych ciągów zero-jedynkowych to 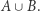 Wykażemy najpierw, że
Wykażemy najpierw, że 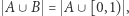 czyli że zbiór wszystkich ciągów jest równoliczny ze zbiorem zawierającym wszystkie ciągi, w których od pewnego miejsca są same jedynki, oraz wszystkie liczby z przedziału
czyli że zbiór wszystkich ciągów jest równoliczny ze zbiorem zawierającym wszystkie ciągi, w których od pewnego miejsca są same jedynki, oraz wszystkie liczby z przedziału 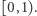
W tym celu musimy rozważyć zapis liczb rzeczywistych w systemie binarnym. Prawdopodobnie każdy Czytelnik zapisywał liczby naturalne w systemie dwójkowym, np. 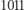 w systemie binarnym to
w systemie binarnym to 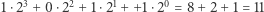 w systemie dziesiętnym. Nie ma jednak żadnych przeciwwskazań, żeby system binarny stosować także po przecinku, np.
w systemie dziesiętnym. Nie ma jednak żadnych przeciwwskazań, żeby system binarny stosować także po przecinku, np. 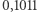 w systemie binarnym to
w systemie binarnym to  Co więcej, podobnie jak każda liczba rzeczywista ma (być może nieskończone) rozwinięcie dziesiętne, tak każdą liczbę rzeczywistą można zapisać w postaci rozwinięcia binarnego. Rozwinięcia skończone oczywiście możemy również napisać jako nieskończone, dodając na końcu same zera
Co więcej, podobnie jak każda liczba rzeczywista ma (być może nieskończone) rozwinięcie dziesiętne, tak każdą liczbę rzeczywistą można zapisać w postaci rozwinięcia binarnego. Rozwinięcia skończone oczywiście możemy również napisać jako nieskończone, dodając na końcu same zera 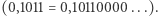 Musimy jednak zauważyć, że podobnie jak w przypadku rozwinięć dziesiętnych, w których od pewnego momentu są same dziewiątki, jeśli w rozwinięciu binarnym od pewnego momentu są same jedynki, mamy do czynienia po prostu z liczbą, którą da się zapisać w skończonym rozwinięciu (na przykład w systemie dziesiętnym
Musimy jednak zauważyć, że podobnie jak w przypadku rozwinięć dziesiętnych, w których od pewnego momentu są same dziewiątki, jeśli w rozwinięciu binarnym od pewnego momentu są same jedynki, mamy do czynienia po prostu z liczbą, którą da się zapisać w skończonym rozwinięciu (na przykład w systemie dziesiętnym 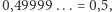 w systemie binarnym
w systemie binarnym 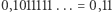 ). Inaczej mówiąc, rozwinięcie w takich przypadkach nie jest jednoznaczne. Wykluczmy więc z rozważań nieskończone rozwinięcia binarne posiadające od pewnego miejsca już same jedynki.
). Inaczej mówiąc, rozwinięcie w takich przypadkach nie jest jednoznaczne. Wykluczmy więc z rozważań nieskończone rozwinięcia binarne posiadające od pewnego miejsca już same jedynki.
Powyższe rozważania definiują metodę ustawienia w pary elementów zbioru 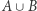 oraz
oraz 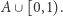 Każdy zero-jedynkowy ciąg, w którym od pewnego miejsca są same jedynki, stawiamy w parę z tym samym ciągiem. W każdym innym przypadku łączymy go w parę z liczbą z przedziału
Każdy zero-jedynkowy ciąg, w którym od pewnego miejsca są same jedynki, stawiamy w parę z tym samym ciągiem. W każdym innym przypadku łączymy go w parę z liczbą z przedziału  której ten ciąg jest rozwinięciem binarnym (dopisujemy do ciągu zero i przecinek z lewej strony). W ten sposób rzeczywiście wykorzystamy wszystkie liczby, każdą jednokrotnie. Mamy więc
której ten ciąg jest rozwinięciem binarnym (dopisujemy do ciągu zero i przecinek z lewej strony). W ten sposób rzeczywiście wykorzystamy wszystkie liczby, każdą jednokrotnie. Mamy więc 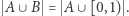
Sprawdźmy teraz, że 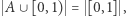 co zakończy nasze rozważania. W tym celu warto zauważyć, że wszystkie elementy zbioru
co zakończy nasze rozważania. W tym celu warto zauważyć, że wszystkie elementy zbioru 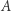 da się zakwaterować w hotelu Hilberta, to jest ponumerować liczbami naturalnymi. Wystarczy najpierw zakwaterować ciąg
da się zakwaterować w hotelu Hilberta, to jest ponumerować liczbami naturalnymi. Wystarczy najpierw zakwaterować ciąg  potem ciąg
potem ciąg 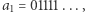 potem dwa ciągi, w których ostatnie zero stoi na drugim miejscu (czyli
potem dwa ciągi, w których ostatnie zero stoi na drugim miejscu (czyli 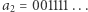 i
i 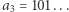 ), następnie te ciągi, gdzie ostatnie zero jest na trzecim miejscu (jest ich cztery!), i tak dalej. Tak więc sporządziliśmy listę wszystkich nieskończonych zero-jedynkowych ciągów, w których od pewnego miejsca są same jedynki,
), następnie te ciągi, gdzie ostatnie zero jest na trzecim miejscu (jest ich cztery!), i tak dalej. Tak więc sporządziliśmy listę wszystkich nieskończonych zero-jedynkowych ciągów, w których od pewnego miejsca są same jedynki, 
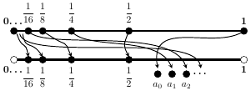
Wybierzmy zatem, podobnie jak poprzednio, ciąg liczb z przedziału ![[0,1]](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/1x-41c43f082f4a6cc1c337d9b1a8ef176ed2abc70e-im-33,33,33-FF,FF,FF.gif) - niech to będzie
- niech to będzie 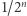 dla
dla 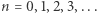 Tym razem musimy poradzić sobie z "nadmiarem" nieskończonej liczby elementów, gdy będziemy łączyć w pary elementy zbioru
Tym razem musimy poradzić sobie z "nadmiarem" nieskończonej liczby elementów, gdy będziemy łączyć w pary elementy zbioru 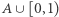 z liczbami z
z liczbami z ![[0,1].](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/5x-41c43f082f4a6cc1c337d9b1a8ef176ed2abc70e-im-33,33,33-FF,FF,FF.gif) Wykorzystajmy więc parzyste potęgi
Wykorzystajmy więc parzyste potęgi 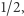 aby znaleźć towarzyszy do par dla tych "dodatkowych" elementów, zaś nieparzyste potęgi muszą nam starczyć jako towarzysze dla dotychczasowych liczb z wybranego ciągu. Zatem liczba
aby znaleźć towarzyszy do par dla tych "dodatkowych" elementów, zaś nieparzyste potęgi muszą nam starczyć jako towarzysze dla dotychczasowych liczb z wybranego ciągu. Zatem liczba  z przedziału
z przedziału ![|[0, 1]](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/8x-41c43f082f4a6cc1c337d9b1a8ef176ed2abc70e-im-33,33,33-FF,FF,FF.gif) nie będąca elementem wybranego ciągu będzie w parze z tą samą liczbą
nie będąca elementem wybranego ciągu będzie w parze z tą samą liczbą  należącą do zbioru
należącą do zbioru 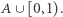 Niech
Niech 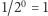 stanie w parze z ciągiem
stanie w parze z ciągiem  ale
ale  niech stoi w parze z
niech stoi w parze z 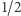 z
z  Następnie
Następnie  trafia do pary z
trafia do pary z 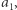 zaś
zaś 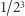 do pary z
do pary z 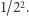 I tak dalej. Inaczej mówiąc, dla każdego
I tak dalej. Inaczej mówiąc, dla każdego 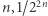 z
z ![[0,1]](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/21x-41c43f082f4a6cc1c337d9b1a8ef176ed2abc70e-im-33,33,33-FF,FF,FF.gif) stoi w parze z ciągiem
stoi w parze z ciągiem 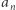 z
z 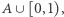 zaś
zaś 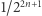 z
z ![[0,1]](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/25x-41c43f082f4a6cc1c337d9b1a8ef176ed2abc70e-im-33,33,33-FF,FF,FF.gif) stoi w parze z liczbą
stoi w parze z liczbą 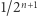 z
z 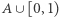 (patrz rysunek). Udało się ustawić wszystko w pary! A zatem
(patrz rysunek). Udało się ustawić wszystko w pary! A zatem ![[0,1] = A](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/28x-41c43f082f4a6cc1c337d9b1a8ef176ed2abc70e-im-33,33,33-FF,FF,FF.gif) czyli zbiór wszystkich liczb rzeczywistych z przedziału
czyli zbiór wszystkich liczb rzeczywistych z przedziału ![[0,1]](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/29x-41c43f082f4a6cc1c337d9b1a8ef176ed2abc70e-im-33,33,33-FF,FF,FF.gif) jest równoliczny ze zbiorem wszystkich nieskończonych ciągów zero-jedynkowych. Wszystkie rozważane przez nas "duże" zbiory też okazały się parami równoliczne.
jest równoliczny ze zbiorem wszystkich nieskończonych ciągów zero-jedynkowych. Wszystkie rozważane przez nas "duże" zbiory też okazały się parami równoliczne.
Mamy zatem w garści różne "małe" zbiory nieskończone, czyli zbiory przeliczalne: 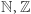 oraz
oraz 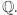 Mamy także zbiory "duże":
Mamy także zbiory "duże": ![|R,[0,1],P(N)](/math/temat/matematyka/teoria_mnogosci/2019/07/31/Zbiory_duze/3x-860a57c7fba457f720bd08f971b7ad1bbd7ef6fc-im-33,33,33-FF,FF,FF.gif) oraz zbiór wszystkich nieskończonych ciągów zero-jedynkowych. Wszystkie takie zbiory, które rozpatrywaliśmy, okazały się parami równoliczne. Zwane są zbiorami mocy continuum. Powstaje więc naturalne pytanie. Czy jest coś pomiędzy zbiorami przeliczalnymi a zbiorami mocy continuum? Czy istnieje zbiór o mocy większej niż moc zbiorów przeliczalnych, a mniejszej niż continuum?
oraz zbiór wszystkich nieskończonych ciągów zero-jedynkowych. Wszystkie takie zbiory, które rozpatrywaliśmy, okazały się parami równoliczne. Zwane są zbiorami mocy continuum. Powstaje więc naturalne pytanie. Czy jest coś pomiędzy zbiorami przeliczalnymi a zbiorami mocy continuum? Czy istnieje zbiór o mocy większej niż moc zbiorów przeliczalnych, a mniejszej niż continuum?
Pytanie takie zadał sobie już Georg Cantor. Nie udało mu się skonstruować takiego zbioru, przypuszczał więc, że zbiór taki nie istnieje, i przez wiele lat swojego życia próbował to udowodnić. Nie był w stanie tego dokonać. Ta niemoc bardzo go frustrowała i dodatkowo źle wpływała na jego chwiejne zdrowie psychiczne. Teza Cantora, że nie istnieje zbiór o mocy większej niż moc zbiorów przeliczalnych, a mniejszej niż continuum, nazywa się hipotezą continuum. Problem zaciekawił wielu matematyków, w tym Davida Hilberta, którego koncepcję nieskończonego hotelu już omawialiśmy. Na Kongresie Matematyków w Paryżu David Hilbert wygłosił referat, podczas którego przedstawił 23 matematyczne problemy (10 z nich zdążył przedstawić ustnie, a reszta pojawiła się w spisanej wersji referatu), jego zdaniem najbardziej interesujące, które powinny zostać rozwiązane w kolejnym stuleciu. Jaki był pierwszy wymieniony przez niego problem? Właśnie hipoteza continuum! Poniżej ten właśnie fragment spisanego już po samym Kongresie referatu Hilberta.

Czy ponad wiek później znamy odpowiedź na pytanie o hipotezę continuum? Jeśli tak, to jaka ona jest? Odpowiedzi na te pytania mogą być zaskakujące! Ale o tym następnym razem.