Mała Delta
Nieskończoność
Nieskończoność
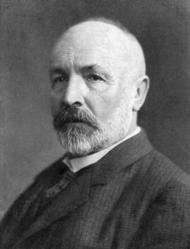
Georg Cantor (1845-1918)
Na nieskończoność natrafiono już w starożytności. Nic dziwnego, że była traktowana z podejrzliwością, w końcu wszystko w prawdziwym świecie wydawało się skończone. Bywała źródłem problemów, paradoksów i sporów (na przykład, paradoks Zenona z Elei). W końcu, w drugiej połowie XIX wieku, nieskończoność udało się nieco oswoić (nie mylić z ujarzmić), weszła do kanonu matematyki, a właściwie w jej fundamenty. Owo oswajanie zaczęło się od Georga Cantora...
Cantor nazwał zbiór przeliczalnym, jeśli jego elementy można ponumerować liczbami naturalnymi. W konsekwencji zbiór liczb naturalnych jest oczywiście przeliczalny, co więcej zbiór liczb całkowitych również (wyjaśnienie w dalszej części). Nieco trudniej wykazać, że przeliczalność dotyczy również zbioru liczb wymiernych. Zupełnym fenomenem była (i jest) praca Georga Cantora Über eine Eigenschaft des Inbegriffs aller reellen algebraischen Zahlen z 1874 roku, w której udowodnił, że choć zbiór liczb algebraicznych - czyli pierwiastków wielomianów o współczynnikach wymiernych, którymi są np. 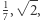 ale
ale 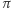 już nie (co jest bardzo nietrywialne) - jest przeliczalny, to zbiór liczb rzeczywistych nie jest.
już nie (co jest bardzo nietrywialne) - jest przeliczalny, to zbiór liczb rzeczywistych nie jest.
W 2018 roku minęła setna rocznica śmierci Georga Cantora (1845-1918), uważanego za ojca teorii mnogości (nauki o zbiorach). Urodził się w Sankt Petersburgu, gdzie mieszkał do 11 roku życia. W młodości uchodził za wybitnego skrzypka. Kiedy rodzina Cantora wróciła do Niemiec w poszukiwaniu łagodniejszego klimatu (z powodu choroby ojca Cantora), odkryto niewiarygodny matematyczny talent chłopca. Dzięki majątkowi odziedziczonemu po ojcu Cantor był w stanie podjąć studia w Berlinie, gdzie napisał pracę doktorską dotyczącą teorii liczb. Habilitację uzyskał na Uniwersytecie w Halle, gdzie później spędził większość swojego naukowego życia i gdzie w 1879 roku został profesorem w wieku 34 lat. W matematycznej karierze natrafiał jednak na liczne przeszkody. Trudności przysparzali mu między innymi niektórzy profesorowie z Berlina, którzy nie godzili się z jego podejściem do matematyki. Działalność naukowa Cantora była w tamtych czasach bardzo kontrowersyjna.
Wspomniane trudności nadszarpnęły zdrowie psychiczne Cantora. Hospitalizowany w 1884 roku, przez pewien czas wolał zajmować się filozofią i literaturą epoki elżbietańskiej, a nie matematyką. Pokonawszy ten kryzys, przyczynił się do powołania Niemieckiego Towarzystwa Matematycznego i został jego pierwszym prezesem. David Hilbert umieścił problem sformułowany przez Cantora, hipotezę continuum, na pierwszym miejscu słynnej listy dwudziestu trzech problemów zebranych podczas Międzynarodowego Kongresu Matematyków w Paryżu w 1900 roku. Jak dzisiaj wiemy, problemu tego sam Cantor mimo licznych prób nie mógł rozwiązać. Ostatnie lata jego życia to na przemian częste pobyty w sanatoriach, problemy finansowe, cenione wykłady i spory o sens stworzonej przez niego teorii mnogości. Zmarł na atak serca w jednym z sanatoriów.
Posługując się słowami Davida Hilberta: prace Cantora to najwspanialszy produkt matematycznego geniuszu i jedno z najwyższych osiągnięć czysto intelektualnej ludzkiej aktywności. Na cześć geniuszu Georga Cantora i jego wpływu na współczesną matematykę, sto lat po jego śmierci, opublikujemy cykl artykułów przybliżających pojęcie nieskończoności i teorię mnogości przez niego stworzoną.