Mała Delta

Hotel Hilberta

Nieskończoność... Co myślisz, gdy słyszysz to słowo? Może myślisz o rozgwieżdżonym niebie? Może próbujesz wyobrazić sobie coś bardzo, ale to bardzo dużego? A może myślisz o ludzkiej wyobraźni i sile naszego umysłu? George Cantor postanowił potraktować nieskończoność jak coś "zwykłego" i po prostu ją zbadał. Pójdziemy jego śladem. Zastanówmy się... Czy każda nieskończoność jest taka sama? Czy też może są większe i mniejsze? Czy wszechświat jest nieskończony? Co to jest nieskończoność? Na wiele pytań dotyczących nieskończoności udzielono wyczerpujących odpowiedzi. Na część z nich odpowiedzi nie są znane. O niektórych wiadomo, że nie da się na nie odpowiedzieć po prostu "tak" lub "nie".

Wybierzmy się do hotelu. Hotel, jak to hotel, jest w nim ileś pokoi - powiedzmy pięć. Przypuśćmy dla uproszczenia, że są jednoosobowe. Nie będzie zaskoczeniem, gdy zauważymy, że jeśli każdy pokój jest zajęty, a na recepcję zgłosi się kolejny gość, zostanie odprawiony z kwitkiem.

Ale... Wyobraź sobie hotel, w którym jest nieskończenie wiele pokoi. Taki eksperyment myślowy zaproponował wspomniany już matematyk, David Hilbert. W Hotelu Hilberta jest nieskończenie wiele jednoosobowych pokoi. Powiedzmy, że są ponumerowane - pierwszy pokój ma numer zero, drugi numer jeden, trzeci numer dwa i tak dalej. Załóżmy, tak jak poprzednio, że w każdym pokoju jest już gość, czyli inaczej rzecz ujmując, wszystkie pokoje są zajęte. Na recepcję w środku nocy zgłasza się jeszcze jeden, spóźniony, chętny do zamieszkania przybysz.

Okazało się, że recepcjonista był matematykiem - zastanowił się dwa razy i udostępnił wolny pokój, budząc uprzednio wszystkich pozostałych gości.

Jak to zrobił? Wszyscy goście zostali poproszeni o przeniesienie się do pokoju o numerze o jeden wyższym niż numer ich obecnego pokoju. W ten sposób gość z pokoju zerowego przeszedł do pokoju pierwszego, gość z pokoju pierwszego do pokoju drugiego, gość z pokoju drugiego do trzeciego i tak dalej. Każdy gość mógł przecież przenieść się do kolejnego pokoju, nic nie stało na przeszkodzie. W wyniku tej operacji pokój zerowy został zwolniony i tam zakwaterował się dodatkowy przybysz. Udało się! Wniosek: w Hotelu Hilberta można zakwaterować o jednego gościa więcej, niż jest miejsc w pokojach. Lub inaczej: zbiór liczb 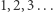$1,2,3...$ jest równoliczny ze zbiorem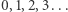 $|0,1,2,3 ...$

Przeprowadźmy jeszcze jeden eksperyment. Załóżmy, że do pustego hotelu zgłaszają się dwie grupy gości: nieskończona grupa kobiet i nieskończona grupa mężczyzn. Jeśli obsługa jest dobrze wychowana, prawdopodobnie wpuści do hotelu najpierw kobiety. Ale niestety, jeśli tak zrobi - zajmą one wszystkie nieskończenie wiele pokoi i nieskończona grupa mężczyzn zostanie na przysłowiowym lodzie. Czy można postąpić inaczej? Owszem. Kwaterować na zmianę. Do zerowego pokoju kobietę, do pierwszego mężczyznę, do drugiego kobietę, do trzeciego mężczyznę itd. W skrócie: w pokojach o parzystych numerach kwaterujemy kobiety, a w pokojach o nieparzystych numerach - mężczyzn. W ten sposób żadnej kobiecie ani żadnemu mężczyźnie nie zabraknie miejsca. Uff... Wniosek: w Hotelu Hilberta zmieszczą się dwie grupy gości, z których każda samodzielnie mogłaby zapełnić cały hotel. Lub inaczej: zbiór liczb 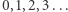$|0,1,2,3...$ jest równoliczny ze zbiorem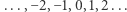 $|...,−2,−1,0,1,2...$

Zastanów się jeszcze, co by się stało, gdyby zamiast "tylko" dwóch nieskończonych grup gości przed Hotelem Hilberta pojawiło się ich nieskończenie wiele, na przykład nieskończenie wiele autobusów, a w każdym nieskończenie wielu pasażerów? Czy można ich przyjąć…? Do tych rozważań jeszcze wrócimy.

A w następnym odcinku przyjrzymy się, jak w dawnych czasach ludzie myśleli o nieskończoności i skąd w ogóle wziął się taki koncept.