Indukcja pozaskończona
Indukcja pozaskończona wykorzystywana jest w dowodach istnienia różnych obiektów matematycznych. Główną częścią tego typu dowodu jest definicja indukcyjna (inaczej: rekurencyjna) funkcji.
Definicje funkcji przez indukcję pozaskończoną są uogólnieniem rekurencyjnych definicji ciągów. Rekurencyjna definicja ciągu 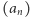 składa się z określenia wyrazu
składa się z określenia wyrazu 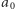 (lub kilku początkowych wyrazów) tego ciągu, a następnie pokazania, w jaki sposób każdy kolejny wyraz
(lub kilku początkowych wyrazów) tego ciągu, a następnie pokazania, w jaki sposób każdy kolejny wyraz 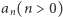 zależy od wyrazów wcześniejszych
zależy od wyrazów wcześniejszych 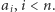 Taką strukturę ma następująca definicja indukcyjna ciągu Fibonacciego:
Taką strukturę ma następująca definicja indukcyjna ciągu Fibonacciego: 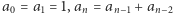 dla
dla 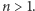 Jest intuicyjnie oczywiste, że powyższa definicja w jednoznaczny sposób definiuje ciąg:
Jest intuicyjnie oczywiste, że powyższa definicja w jednoznaczny sposób definiuje ciąg: 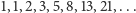
W następnym przykładzie definicja indukcyjna pewnego ciągu posłuży nam do dowodu istnienia funkcji  ze zbioru liczb wymiernych w liczby wymierne (oznaczane przez
ze zbioru liczb wymiernych w liczby wymierne (oznaczane przez 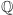 ), która liczby wymierne każdego przedziału
), która liczby wymierne każdego przedziału 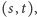 gdzie
gdzie 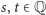 i
i 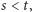 przekształca na cały zbiór
przekształca na cały zbiór 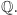 Zatem funkcja
Zatem funkcja 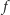 ma mieć tę własność, że dla każdej trójki liczb wymiernych
ma mieć tę własność, że dla każdej trójki liczb wymiernych 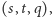 gdzie
gdzie 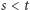 (oznaczmy zbiór wszystkich takich trójek przez
(oznaczmy zbiór wszystkich takich trójek przez 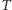 ), istnieje taka liczba
), istnieje taka liczba 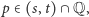 że
że 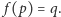
Skorzystamy z tego, że 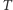 jest zbiorem przeliczalnym, czyli takim, którego elementy można ponumerować liczbami naturalnymi. Innymi słowy, istnieje ciąg trójek
jest zbiorem przeliczalnym, czyli takim, którego elementy można ponumerować liczbami naturalnymi. Innymi słowy, istnieje ciąg trójek 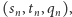 gdzie
gdzie 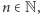 którego zbiorem wyrazów jest
którego zbiorem wyrazów jest 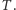 Za jego pomocą indukcyjnie zdefiniujemy ciąg
Za jego pomocą indukcyjnie zdefiniujemy ciąg 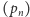 taki, że
taki, że 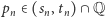 oraz
oraz 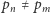 dla wszystkich
dla wszystkich 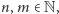 o ile
o ile 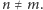 Mianowicie, określamy najpierw
Mianowicie, określamy najpierw 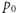 jako dowolną liczbę wymierną z przedziału
jako dowolną liczbę wymierną z przedziału 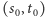 (np.
(np. 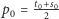 ). Następnie, jeśli
). Następnie, jeśli 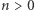 i dane są już wyrazy
i dane są już wyrazy 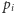 dla
dla 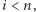 to definiujemy
to definiujemy 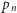 jako jedną z tych liczb wymiernych przedziału
jako jedną z tych liczb wymiernych przedziału 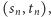 które są różne od każdego
które są różne od każdego 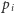 dla
dla 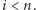 Wybór
Wybór 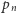 jest możliwy, ponieważ w każdym niepustym przedziale otwartym jest nieskończenie wiele liczb wymiernych.
jest możliwy, ponieważ w każdym niepustym przedziale otwartym jest nieskończenie wiele liczb wymiernych.
Mając dany ciąg 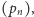 określamy funkcję
określamy funkcję 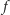 na wszystkich jego wyrazach jako
na wszystkich jego wyrazach jako 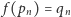 dla
dla 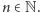 To gwarantuje, że funkcja
To gwarantuje, że funkcja 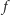 ma żądaną własność: każda trójka
ma żądaną własność: każda trójka 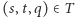 jest postaci
jest postaci 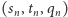 dla pewnego
dla pewnego 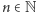 i wówczas
i wówczas 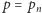 jest tą liczbą wymierną z przedziału
jest tą liczbą wymierną z przedziału 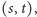 dla której
dla której 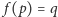 (na pozostałych liczbach wymiernych, jeśli takie istnieją, można określić wartości funkcji
(na pozostałych liczbach wymiernych, jeśli takie istnieją, można określić wartości funkcji 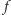 jakkolwiek).
jakkolwiek).
Zmodyfikujemy teraz powyższe rozumowanie tak, by uzyskać funkcję 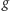 ze zbioru liczb rzeczywistych w liczby rzeczywiste (oznaczane przez
ze zbioru liczb rzeczywistych w liczby rzeczywiste (oznaczane przez 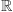 ), która każdy przedział
), która każdy przedział 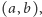 gdzie
gdzie 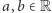 i
i 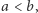 przekształca na cały zbiór
przekształca na cały zbiór 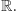 Znanych jest wiele dowodów istnienia takiej funkcji. Przedstawimy tu argument oparty na indukcji pozaskończonej.
Znanych jest wiele dowodów istnienia takiej funkcji. Przedstawimy tu argument oparty na indukcji pozaskończonej.
Niech 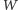 będzie zbiorem wszystkich takich trójek liczb rzeczywistych
będzie zbiorem wszystkich takich trójek liczb rzeczywistych 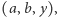 że
że 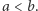 Jest on nieprzeliczalny, nie możemy więc jego elementów ponumerować liczbami naturalnymi. Skorzystamy jednak z tego, że istnieje (czego nie będziemy tu dowodzić) wygodny z punktu widzenia naszej sytuacji odpowiednik zbioru liczb naturalnych, mianowicie zbiór, który oznaczymy przez
Jest on nieprzeliczalny, nie możemy więc jego elementów ponumerować liczbami naturalnymi. Skorzystamy jednak z tego, że istnieje (czego nie będziemy tu dowodzić) wygodny z punktu widzenia naszej sytuacji odpowiednik zbioru liczb naturalnych, mianowicie zbiór, który oznaczymy przez 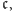 wraz z relacją
wraz z relacją 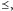 ustalającą pewien liniowy porządek jego elementów, o następujących własnościach:
ustalającą pewien liniowy porządek jego elementów, o następujących własnościach:
- 1.
- Wszystkie elementy zbioru
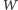 można poindeksować za pomocą elementów zbioru
można poindeksować za pomocą elementów zbioru 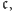 czyli ustawić w ciąg pozaskończony trójek
czyli ustawić w ciąg pozaskończony trójek 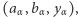 gdzie
gdzie 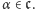
- 2.
- Jeśli
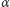 jest dowolnym elementem zbioru
jest dowolnym elementem zbioru 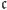 oraz
oraz 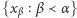 jest dowolnym zbiorem złożonym z liczb rzeczywistych, poindeksowanych elementami zbioru
jest dowolnym zbiorem złożonym z liczb rzeczywistych, poindeksowanych elementami zbioru 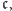 mniejszymi w sensie porządku
mniejszymi w sensie porządku  od
od 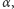 to w każdym przedziale
to w każdym przedziale 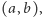 gdzie
gdzie 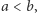 znajdzie się liczba różna od wszystkich liczb
znajdzie się liczba różna od wszystkich liczb 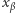 dla
dla 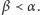
- 3.
- W każdym niepustym podzbiorze zbioru
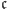 istnieje element najmniejszy w sensie porządku
istnieje element najmniejszy w sensie porządku 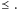
Z pomocą ciągu pozaskończonego 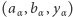 (zob. warunek 1) przez indukcję pozaskończoną zdefiniujemy taki ciąg pozaskończony
(zob. warunek 1) przez indukcję pozaskończoną zdefiniujemy taki ciąg pozaskończony 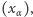 że
że 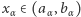 oraz
oraz 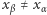 dla wszystkich
dla wszystkich 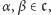 o ile
o ile 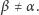 Postępujemy zgodnie ze schematem wcześniejszej konstrukcji ciągu
Postępujemy zgodnie ze schematem wcześniejszej konstrukcji ciągu 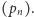 Mianowicie, jeśli
Mianowicie, jeśli 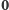 oznacza najmniejszy w sensie porządku
oznacza najmniejszy w sensie porządku 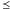 element zbioru
element zbioru 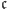 (taki element istnieje na mocy warunku 3), to określamy najpierw
(taki element istnieje na mocy warunku 3), to określamy najpierw 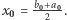 Następnie, jeśli
Następnie, jeśli 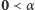 i dane są już wyrazy
i dane są już wyrazy 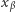 dla
dla 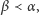 to definiujemy
to definiujemy 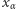 jako jedną z tych liczb z przedziału
jako jedną z tych liczb z przedziału 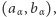 które są różne od każdego
które są różne od każdego 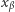 dla
dla 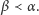 Wybór
Wybór 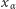 jest możliwy na mocy warunku 2.
jest możliwy na mocy warunku 2.
Wymaga jeszcze uzasadnienia, dlaczego opisana powyżej definicja indukcyjna prowadzi do jednoznacznego przypisania wartości 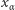 wszystkim
wszystkim 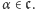 Nieco upraszczając, gdyby zbiór tych
Nieco upraszczając, gdyby zbiór tych 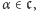 którym powyższa definicja indukcyjna nie przypisała wartości, był niepusty, to na mocy warunku 3. istniałby w nim najmniejszy element, powiedzmy
którym powyższa definicja indukcyjna nie przypisała wartości, był niepusty, to na mocy warunku 3. istniałby w nim najmniejszy element, powiedzmy 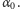 Wówczas
Wówczas 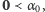 gdyż wyraz
gdyż wyraz 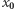 został zdefiniowany. Ponadto, na mocy definicji
został zdefiniowany. Ponadto, na mocy definicji 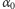 zdefiniowane byłyby wszystkie wyrazy
zdefiniowane byłyby wszystkie wyrazy 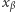 dla
dla 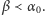 To jednak - jak widzieliśmy powyżej - umożliwiałoby zdefiniowanie wyrazu
To jednak - jak widzieliśmy powyżej - umożliwiałoby zdefiniowanie wyrazu 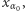 co prowadziłoby do sprzeczności z definicją elementu
co prowadziłoby do sprzeczności z definicją elementu 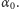
Na koniec, mając dany ciąg pozaskończony 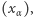 określamy funkcję
określamy funkcję 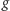 na wszystkich jego wyrazach jako
na wszystkich jego wyrazach jako 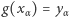 dla każdego
dla każdego 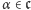 (por. warunek 1). Podobnie jak w przypadku funkcji
(por. warunek 1). Podobnie jak w przypadku funkcji 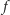 to już wystarczy, by funkcja
to już wystarczy, by funkcja 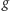 miała żądaną własność, co kończy dowód.
miała żądaną własność, co kończy dowód.