Czy trzeba dowodzić rzeczy oczywistych?
Każda nauka ścisła ma własne metody potwierdzania swoich tez. Dla większości z nich weryfikacja twierdzeń polega na konfrontacji z rzeczywistością. Matematyka jest jedyną z tych nauk, w której owa rzeczywistość nie jest ostateczną (ani jakąkolwiek) metodą sprawdzania zdań aspirujących do wzbogacenia zasobu wiedzy matematycznej. Weryfikatorem twierdzeń jest dowód. Mowa tu o tzw. matematyce czystej lub teoretycznej; zauważmy jednak, że fizyczna rzeczywistość weryfikuje stosowalność instrumentów matematycznych, nie ich wartość matematyczną.
Zawodowy matematyk, niezajmujący się logiką lub podstawami matematyki, nie jest zainteresowany ścisłą odpowiedzią na powyższe pytania. O poprawności rozumowania i wyprowadzonych wniosków zaświadcza środowisko, czyli inni matematycy, którzy, czytając zapis takiego rozumowania, uznają je za wystarczające do stwierdzenia poprawności wyniku lub nie. Odwołują się przy tym do intuicyjnego rozumienia terminów, o których mowa w poprzednim akapicie. W szczególności znają odpowiedź na pytanie o pierwsze zdanie rozumowania (jedno lub kilka): ma to być zdanie wcześniej już uznane za twierdzenie lub aksjomat. Dowód jest zatem rozumowaniem, w którym wychodzimy od zdań już uznanych i, stosując poprawne wnioskowanie, dochodzimy do zdania, które chcemy - i możemy - dołączyć do teorii.
Dopóki jednak odwołujemy się do intuicji, musimy się pogodzić z faktem, że może ona działać różnie u różnych ludzi. Co robić, gdy występuje rozbieżność między intuicjami? I tu metoda jest mocno ugruntowana w praktyce: należy rozbić dowód na mniejsze, coraz mniejsze fragmenty tak długo, aż nikt z oceniających nie będzie miał wątpliwości, że każde zdanie rzeczywiście daje się wyprowadzić z poprzednich zgodnie z ogólnymi regułami. A niżej, jak siatka zabezpieczająca wyczyny cyrkowców na wysoko zawieszonych linach, jest formalne pojęcie dowodu w teorii formalnej: to ciąg formuł w (symbolicznym) języku tej teorii taki, że każda formuła jest albo aksjomatem, albo wynika z poprzednich na mocy jednej z przyjętych reguł wnioskowania. Przypomnijmy, że użyte tu pojęcia składników teorii formalnej muszą być jednoznacznie zdefiniowane (tu tylko w poglądowym skrócie): dla ustalonego alfabetu formuła jest wyrażeniem zbudowanym z symboli języka za pomocą ściśle określonych zasad, aksjomat jest wybraną formułą, reguła wnioskowania to zasada pozwalająca przejść od jednych wyrażeń (formuł) do innych, zwanych wnioskami z poprzednich. Działając w teorii formalnej, nie odwołujemy się do znaczeń symboli alfabetu, formuł itp. - przekształcamy je zgodnie z formalnymi regułami.
Co to jest oczywistość?
"Oczywistość" jest - oczywiście - sprawą subiektywną, jednak bardzo często jesteśmy zgodni co do oczywistości wielu faktów matematycznych. Na ogół oznacza to, że albo dowód takiego faktu jest na tyle prosty, że od razu go widzimy oczyma rozumu, albo dowód twierdzenia widzieliśmy już tyle razy, że nie musimy się wciąż do niego odwoływać, by użyć danego twierdzenia. Bywają jednak sytuacje, kiedy tylko wydaje nam się, że sprawa jest oczywista. Podejrzewam, że jeśli nie każdy, to prawie każdy matematyk ma za sobą doświadczenie nadmiernej wiary w oczywistość jakiegoś stwierdzenia, które okazywało się fałszywe, a w najlepszym razie - daleko nieoczywiste. Złudne oczywistości wynikają jednak także z nadinterpretacji pojęć. Trudno w tej kwestii wysnuwać ogólne konkluzje, popatrzmy zatem na przykład, którego dostarcza teoria mnogości.
Teoria mnogości bywa źródłem wielu pokus uznania rzeczy za oczywiste. Czyż nie jest oczywiste, że liczb rzeczywistych jest więcej niż naturalnych? Po co dowodzić, że zbiór ma więcej podzbiorów niż elementów? Co gorsza, czyż nie jest oczywiste, że liczb wymiernych jest więcej niż liczb naturalnych? Pokusa kryje się w słowie więcej.

Za przykład niech posłuży twierdzenie Cantora-Bernsteina, zasługujące na miano młota na biednych (matematycznie) studentów. Sformułujmy je w wersji łagodnej (gdzie 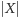 oznacza moc zbioru
oznacza moc zbioru 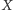 ):
):
Twierdzenie (wersja 1). Jeśli 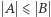 oraz
oraz 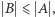 to
to 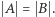
Podejrzenie oczywistości bierze się, rzecz jasna, z błędnej interpretacji symbolu 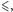 kojarzonego ze "zwykłą", liczbową niewiększością, dla której podobne twierdzenie mamy niemal we krwi. Pokusa znika, gdy sformułujemy twierdzenie w sposób ujawniający znaczenie tego symbolu:
kojarzonego ze "zwykłą", liczbową niewiększością, dla której podobne twierdzenie mamy niemal we krwi. Pokusa znika, gdy sformułujemy twierdzenie w sposób ujawniający znaczenie tego symbolu:
Twierdzenie (wersja 2). Jeśli istnieje funkcja różnowartościowa ze zbioru 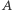 w zbiór
w zbiór 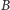 oraz istnieje funkcja różnowartościowa ze zbioru
oraz istnieje funkcja różnowartościowa ze zbioru 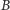 w zbiór
w zbiór 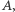 to istnieje bijekcja ze zbioru
to istnieje bijekcja ze zbioru 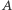 w zbiór
w zbiór 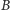 (czyli połączenie elementów zbioru
(czyli połączenie elementów zbioru 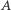 i elementów zbioru
i elementów zbioru 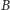 w rozłączne pary).
w rozłączne pary).
Teraz twierdzenie wydaje się nieco mniej oczywiste - ale może jednak nie? W takim razie popatrzmy na dowód - w wersji rzadziej pokazywanej na wykładach z tzw. wstępu do matematyki.
Dowód "oczywistego" twierdzenia Cantora-Bernsteina
Dowód twierdzenia Cantora-Bernsteina wyprowadzimy z dwóch twierdzeń pomocniczych, ciekawych samych w sobie (niżej 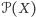 oznacza zbiór wszystkich podzbiorów zbioru
oznacza zbiór wszystkich podzbiorów zbioru 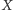 ).
).
Twierdzenie (Tarski). Niech 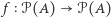 będzie funkcją taką, że jeśli
będzie funkcją taką, że jeśli 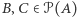 oraz
oraz 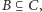 to
to 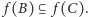 Wówczas istnieje punkt stały funkcji
Wówczas istnieje punkt stały funkcji 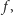 czyli istnieje
czyli istnieje 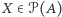 taki, że
taki, że 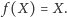
Szkic (a raczej zachęta do) dowodu. Niech 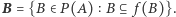 Wówczas
Wówczas 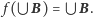 (
( 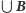 oznacza sumę wszystkich zbiorów z rodziny
oznacza sumę wszystkich zbiorów z rodziny 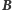 ).
).

Lemat (Banach). Niech 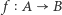 oraz
oraz 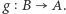 Wówczas istnieją rozłączne zbiory
Wówczas istnieją rozłączne zbiory 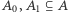 oraz rozłączne zbiory
oraz rozłączne zbiory 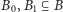 takie, że
takie, że 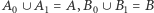 oraz
oraz 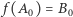 i
i 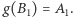
Szkic (a raczej zachęta do) dowodu. Niech  dla
dla 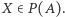 Wówczas funkcja
Wówczas funkcja 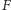 spełnia założenia twierdzenia Tarskiego, istnieje zatem zbiór
spełnia założenia twierdzenia Tarskiego, istnieje zatem zbiór 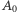 taki, że
taki, że 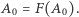 Wystarczy teraz przyjąć
Wystarczy teraz przyjąć 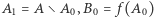 oraz
oraz 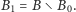
Dowód twierdzenia Cantora-Bernsteina. Niech 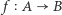 oraz
oraz 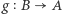 będą funkcjami różnowartościowymi. Wówczas istnieją rozłączne zbiory
będą funkcjami różnowartościowymi. Wówczas istnieją rozłączne zbiory 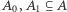 oraz rozłączne zbiory
oraz rozłączne zbiory 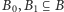 (na mocy lematu Banacha) takie, że
(na mocy lematu Banacha) takie, że 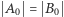 oraz
oraz 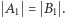 Stąd wynika równoliczność zbiorów
Stąd wynika równoliczność zbiorów 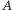 i
i