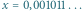Deltoid
Równe i różne nieskończoności
Czy nieskończoność jest tylko jedna? Nie, istnieją różne, większe i mniejsze!
Zbiory 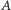 i
i 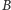 są równoliczne, gdy ich elementy można dobrać w pary (każdy element z
są równoliczne, gdy ich elementy można dobrać w pary (każdy element z 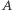 ma dokładnie jedną parę w
ma dokładnie jedną parę w 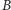 i na odwrót). Piszemy wtedy
i na odwrót). Piszemy wtedy 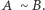 Jeśli
Jeśli 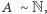 to zbiór
to zbiór 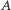 nazywamy przeliczalnym; dobranie w pary jego elementów z liczbami naturalnymi odpowiada ustawieniu ich w ciąg:
nazywamy przeliczalnym; dobranie w pary jego elementów z liczbami naturalnymi odpowiada ustawieniu ich w ciąg: 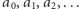 (element zbioru
(element zbioru  oznaczony jako
oznaczony jako 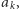 jest w parze z liczbą naturalną
jest w parze z liczbą naturalną 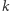 ).
).
Zakładamy, że 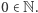
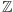 oznacza zbiór liczb całkowitych,
oznacza zbiór liczb całkowitych, 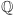 to zbiór liczb wymiernych,
to zbiór liczb wymiernych, 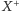 oznacza zbiór dodatnich liczb z
oznacza zbiór dodatnich liczb z 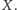
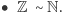 Udowodnimy, że liczb całkowitych, wbrew pozorom, nie jest wcale więcej, niż naturalnych, a dokładnie tyle samo. W tym celu ustawmy je w następujący ciąg:
Udowodnimy, że liczb całkowitych, wbrew pozorom, nie jest wcale więcej, niż naturalnych, a dokładnie tyle samo. W tym celu ustawmy je w następujący ciąg: 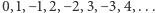 Każda liczba całkowita występuje w tym ciągu dokładnie jeden raz, jest ich więc tyle samo, co liczb naturalnych.
Każda liczba całkowita występuje w tym ciągu dokładnie jeden raz, jest ich więc tyle samo, co liczb naturalnych.
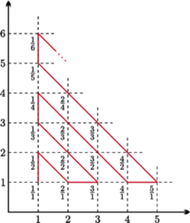
Rys. 1 Zygzak odwiedza dokładnie raz każdy punkt 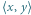 dla
dla 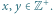
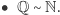 Wykażemy teraz, że również liczb wymiernych jest przeliczalnie wiele. Najpierw udowodnimy, że
Wykażemy teraz, że również liczb wymiernych jest przeliczalnie wiele. Najpierw udowodnimy, że 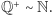 W tym celu rozważmy punkty płaszczyzny o obu współrzędnych całkowitych dodatnich. Każdemu takiemu punktowi
W tym celu rozważmy punkty płaszczyzny o obu współrzędnych całkowitych dodatnich. Każdemu takiemu punktowi  przypiszmy dodatnią liczbę wymierną
przypiszmy dodatnią liczbę wymierną  Następnie odwiedźmy po kolei wszystkie te punkty, spacerując po płaszczyźnie zygzakiem o początku w
Następnie odwiedźmy po kolei wszystkie te punkty, spacerując po płaszczyźnie zygzakiem o początku w 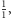 jak na rysunku 1. Spisujmy kolejno odwiedzane liczby wymierne
jak na rysunku 1. Spisujmy kolejno odwiedzane liczby wymierne 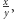 ale bez powtórzeń (np. liczbę
ale bez powtórzeń (np. liczbę 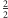 pomijamy, bo wcześniej była
pomijamy, bo wcześniej była 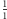 ). Otrzymujemy w ten sposób ciąg wszystkich dodatnich liczb wymiernych:
). Otrzymujemy w ten sposób ciąg wszystkich dodatnich liczb wymiernych: 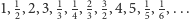
Aby wykazać, że 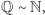 zastosujmy podobny pomysł, jak przy dowodzie
zastosujmy podobny pomysł, jak przy dowodzie 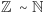 - ustawmy na przemian liczby z powyższego ciągu i liczby do nich przeciwne, a na początku zero:
- ustawmy na przemian liczby z powyższego ciągu i liczby do nich przeciwne, a na początku zero: 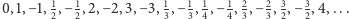
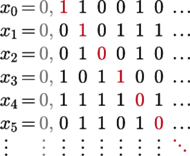
Rys. 2 Przykładowe wartości ciągu 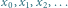 oraz przekątna tabeli. Tutaj
oraz przekątna tabeli. Tutaj 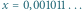
 Liczb rzeczywistych jest więcej, niż liczb naturalnych, czyli nieprzeliczalnie wiele. Wykażemy, że nieprzeliczalny jest już podzbiór takich liczb z odcinka
Liczb rzeczywistych jest więcej, niż liczb naturalnych, czyli nieprzeliczalnie wiele. Wykażemy, że nieprzeliczalny jest już podzbiór takich liczb z odcinka 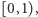 których rozwinięcie dziesiętne składa się wyłącznie z cyfr 0 i 1.
których rozwinięcie dziesiętne składa się wyłącznie z cyfr 0 i 1.
Załóżmy, że podzbiór ten jest przeliczalny, czyli jego elementy można ustawić w ciąg 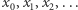 Otrzymujemy tabelę (Rys. 2); jest ona nieskończona w prawo (liczbom o skończonym rozwinięciu dziesiętnym dopisujemy dalej same zera) oraz w dół (liczb rozważanej postaci jest nieskończenie wiele, m.in.
Otrzymujemy tabelę (Rys. 2); jest ona nieskończona w prawo (liczbom o skończonym rozwinięciu dziesiętnym dopisujemy dalej same zera) oraz w dół (liczb rozważanej postaci jest nieskończenie wiele, m.in. 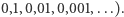
Zapiszmy ciąg cyfr z przekątnej tabeli, a następnie zamieńmy w nim wszystkie 0 na 1, a 1 na 0. Niech liczba  ma w zapisie dziesiętnym zero, a po przecinku uzyskany w ten sposób ciąg cyfr. Wtedy
ma w zapisie dziesiętnym zero, a po przecinku uzyskany w ten sposób ciąg cyfr. Wtedy  oraz
oraz  ma w rozwinięciu dziesiętnym same 0 i 1, zatem z założenia występuje w naszym ciągu
ma w rozwinięciu dziesiętnym same 0 i 1, zatem z założenia występuje w naszym ciągu 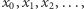 czyli w którymś wierszu rozważanej tabeli. Nie jest on równy
czyli w którymś wierszu rozważanej tabeli. Nie jest on równy  bo wskutek zamiany 0 i 1 z przekątnej, od liczby w pierwszym wierszu różni się na pierwszym miejscu po przecinku. Podobnie
bo wskutek zamiany 0 i 1 z przekątnej, od liczby w pierwszym wierszu różni się na pierwszym miejscu po przecinku. Podobnie  bo od liczby w drugim wierszu różni się na drugim miejscu po przecinku. Analogicznie
bo od liczby w drugim wierszu różni się na drugim miejscu po przecinku. Analogicznie 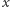 nie jest równy żadnej z pozostałych liczb z naszego ciągu, bo od liczby w
nie jest równy żadnej z pozostałych liczb z naszego ciągu, bo od liczby w 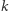 -tym wierszu różni się na
-tym wierszu różni się na 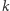 -tym miejscu po przecinku. Zbudowaliśmy więc liczbę z rozważanego zbioru, ale spoza ciągu, który miał zawierać wszystkie jego elementy. Uzyskana sprzeczność dowodzi, że zbiór ten jest nieprzeliczalny, zatem także
-tym miejscu po przecinku. Zbudowaliśmy więc liczbę z rozważanego zbioru, ale spoza ciągu, który miał zawierać wszystkie jego elementy. Uzyskana sprzeczność dowodzi, że zbiór ten jest nieprzeliczalny, zatem także 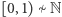 oraz
oraz 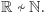
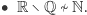 Gdyby liczb niewymiernych było przeliczalnie wiele, można by ustawić je w ciąg
Gdyby liczb niewymiernych było przeliczalnie wiele, można by ustawić je w ciąg 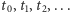 Wykorzystując nasz ciąg liczb wymiernych, uzyskalibyśmy ciąg wszystkich liczb rzeczywistych:
Wykorzystując nasz ciąg liczb wymiernych, uzyskalibyśmy ciąg wszystkich liczb rzeczywistych: 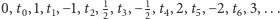 Wiemy jednak, że
Wiemy jednak, że 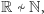 zatem to niemożliwe. Stąd
zatem to niemożliwe. Stąd 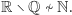

Rys. 3
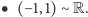 Pokażemy teraz, że odcinek zawiera tyle samo punktów, co prosta. Najpierw wykażemy, że
Pokażemy teraz, że odcinek zawiera tyle samo punktów, co prosta. Najpierw wykażemy, że 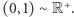 Rozważmy odcinek
Rozważmy odcinek 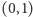 na osi
na osi 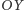 oraz dodatnią półoś
oraz dodatnią półoś 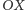 (Rys. 3). Zapalmy latarkę w punkcie
(Rys. 3). Zapalmy latarkę w punkcie 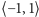 i każdemu punktowi z odcinka
i każdemu punktowi z odcinka 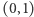 przydzielmy do pary jego cień na półprostej
przydzielmy do pary jego cień na półprostej 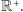
Analogicznie, punktom z odcinka ![(− 1,0]](/math/temat/matematyka/teoria_mnogosci/2013/06/29/Rowne_i_rozne_nieskonczonosci/1x-3d4290773d46ec3ec72177720de990cce94141d2-im-33,33,33-FF,FF,FF.gif) przydzielamy pary z niedodatniej półosi
przydzielamy pary z niedodatniej półosi  (latarka w punkcie
(latarka w punkcie 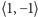 ), co wobec powyższego daje
), co wobec powyższego daje 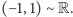
Twierdzenie Cantora orzeka, że każdy zbiór ma więcej podzbiorów niż elementów. Stąd dla dowolnego zbioru nieskończonego istnieje zbiór jeszcze od niego większy! Opisane powyżej zbiory, równoliczne z 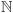 lub
lub 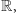 to tylko niektórzy, najczęściej spotykani przedstawiciele zbiorów nieskończonych.
to tylko niektórzy, najczęściej spotykani przedstawiciele zbiorów nieskończonych.
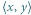 dla
dla 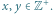
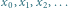 oraz przekątna tabeli. Tutaj
oraz przekątna tabeli. Tutaj