Kaskady i swaty
Często pojawiające się w matematyce zadanie polega na skonstruowaniu funkcji
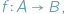 spełniającej pewne warunki. Między innymi możemy chcieć,
aby funkcja ta była różnowartościowa i „na”, co gdyby miało miejsce,
oznaczałoby równoliczność zbiorów
spełniającej pewne warunki. Między innymi możemy chcieć,
aby funkcja ta była różnowartościowa i „na”, co gdyby miało miejsce,
oznaczałoby równoliczność zbiorów
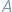 i
i
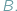 Punktem wyjścia
bywa inna funkcja
Punktem wyjścia
bywa inna funkcja
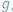 która potrzebnych warunków nie spełnia, ale
wystarczy ją tylko trochę zmienić.
która potrzebnych warunków nie spełnia, ale
wystarczy ją tylko trochę zmienić.
Przypuśćmy, że mamy taką funkcję
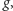 dla której istnieje tylko jedna para
elementów
dla której istnieje tylko jedna para
elementów
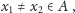 taka że
taka że
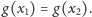 Wtedy możemy
wybrać
Wtedy możemy
wybrać
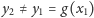 i przyjąć
i przyjąć
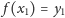 i
i
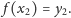 Jeśli
istnieje
Jeśli
istnieje
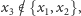 takie że
takie że
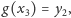 to wybieramy
to wybieramy
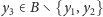 i przyjmujemy
i przyjmujemy
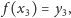 itd. Przyjęcie wartości
itd. Przyjęcie wartości
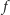 dla pewnego
dla pewnego
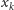 „strąca” przywiązanie elementu
„strąca” przywiązanie elementu
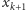 do
elementu
do
elementu
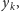 będącego wartością funkcji
będącego wartością funkcji
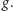 Nazwiemy to
kaskadą.
Nazwiemy to
kaskadą.
Najprostszym zastosowaniem przedstawionego wyżej sposobu jest
udowodnienie, że odcinki
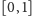 i
i
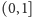 mają tyle samo
punktów. Zaczynając od funkcji
mają tyle samo
punktów. Zaczynając od funkcji
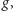 takiej że
takiej że
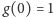 oraz
oraz
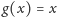 dla każdego
dla każdego
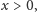 określamy funkcję
określamy funkcję
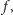 taką
że dla każdego
taką
że dla każdego
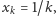 gdzie
gdzie
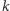 jest liczbą naturalną,
przyjmujemy
jest liczbą naturalną,
przyjmujemy
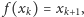 a dla każdego
a dla każdego
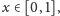 które nie
jest tej postaci, przyjmujemy
które nie
jest tej postaci, przyjmujemy
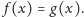
Użyjemy metody kaskadowej do udowodnienia twierdzenia Halla, znanego też pod nazwą twierdzenia o małżeństwach. Najpierw przypomnijmy problem.
Mamy dane dwa zbiory skończone
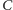 i
i
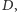 których elementy
możemy wyobrazić sobie jako chłopców i dziewczyny. Mamy wyswatać
chłopców, przy czym każdy z nich ma określony zbiór kandydatek na żonę
(upraszczając, powiemy, że je zna), będący podzbiorem zbioru
których elementy
możemy wyobrazić sobie jako chłopców i dziewczyny. Mamy wyswatać
chłopców, przy czym każdy z nich ma określony zbiór kandydatek na żonę
(upraszczając, powiemy, że je zna), będący podzbiorem zbioru
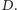 Żonę,
oczywiście, można mieć tylko jedną, podobnie żadna dziewczyna nie
może mieć więcej niż jednego męża. Potrzebna jest zatem funkcja
różnowartościowa
Żonę,
oczywiście, można mieć tylko jedną, podobnie żadna dziewczyna nie
może mieć więcej niż jednego męża. Potrzebna jest zatem funkcja
różnowartościowa
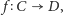 taka że każdy chłopiec
taka że każdy chłopiec
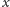 zna
dziewczynę
zna
dziewczynę
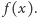 Taką funkcję
Taką funkcję
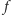 nazywamy skojarzeniem
o liczności równej liczbie chłopców
nazywamy skojarzeniem
o liczności równej liczbie chłopców
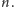
Znajdowanie skojarzenia jest oczywiście problemem grafowym; mamy tu graf
dwudzielny, którego każda krawędź łączy chłopca i dziewczynę, którzy się
znają. Skojarzenie można utożsamić z odpowiednim podzbiorem krawędzi.
Twierdzenie Halla mówi, że skojarzenie o liczności
 istnieje (czyli
wszystkich chłopców można wyswatać) wtedy i tylko wtedy, gdy dla
każdego
istnieje (czyli
wszystkich chłopców można wyswatać) wtedy i tylko wtedy, gdy dla
każdego
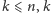 dowolnie wybranych chłopców zna w sumie co
najmniej
dowolnie wybranych chłopców zna w sumie co
najmniej
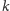 dziewczyn.
dziewczyn.
Konieczność tego warunku (oznaczymy go
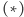 ) dla istnienia skojarzenia
o liczności
) dla istnienia skojarzenia
o liczności
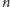 jest oczywista (kto nie jest tego pewny, może przypomni
sobie o zasadzie szufladkowej Dirichleta). Udowodnimy, że warunek
jest oczywista (kto nie jest tego pewny, może przypomni
sobie o zasadzie szufladkowej Dirichleta). Udowodnimy, że warunek
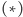 jest wystarczający, używając indukcji.
jest wystarczający, używając indukcji.
Jeśli
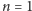 i chłopiec zna co najmniej jedną dziewczynę, to można go
wyswatać. Przypuśćmy zatem, że
i chłopiec zna co najmniej jedną dziewczynę, to można go
wyswatać. Przypuśćmy zatem, że
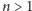 i twierdzenie jest prawdziwe
dla
i twierdzenie jest prawdziwe
dla
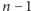 chłopców, a ponadto dla ustalonego zbioru
chłopców, a ponadto dla ustalonego zbioru
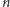 chłopców
warunek (*) jest spełniony. Tym bardziej jest on spełniony, jeśli pominiemy
jednego (dowolnego) chłopca. Możemy więc znaleźć dziewczyny dla
pozostałych
chłopców
warunek (*) jest spełniony. Tym bardziej jest on spełniony, jeśli pominiemy
jednego (dowolnego) chłopca. Możemy więc znaleźć dziewczyny dla
pozostałych
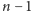 chłopców. Pary na razie zaręczamy (zaręczyny, jeśli
trzeba, będzie można zerwać). Spróbujemy teraz wyswatać
chłopców. Pary na razie zaręczamy (zaręczyny, jeśli
trzeba, będzie można zerwać). Spróbujemy teraz wyswatać
 -tego
chłopca; utworzymy z niego zbiór jednoelementowy
-tego
chłopca; utworzymy z niego zbiór jednoelementowy
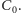 Niech
Niech
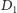 oznacza zbiór tych dziewczyn, które
oznacza zbiór tych dziewczyn, które
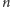 -ty chłopiec zna. Zbiór
-ty chłopiec zna. Zbiór
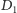 jest niepusty z uwagi na warunek
jest niepusty z uwagi na warunek
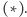 Jeśli jedna z tych
dziewczyn nie ma narzeczonego, to możemy ją zaręczyć z
Jeśli jedna z tych
dziewczyn nie ma narzeczonego, to możemy ją zaręczyć z
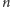 -tym
chłopcem. W przeciwnym razie niech
-tym
chłopcem. W przeciwnym razie niech
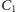 oznacza zbiór chłopców
zaręczonych z dziewczynami z
oznacza zbiór chłopców
zaręczonych z dziewczynami z
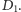 Niech teraz
Niech teraz
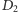 oznacza zbiór
tych dziewczyn, które znają chłopców ze zbioru
oznacza zbiór
tych dziewczyn, które znają chłopców ze zbioru
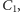 ale nie są z nimi
zaręczone.
ale nie są z nimi
zaręczone.
Jeśli któraś z nich nie ma narzeczonego, to możemy znaleźć
w
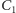 chłopca, który ją zna, odwołać jego dotychczasowe zaręczyny
i zaręczyć z tą dziewczyną. Wtedy w zbiorze
chłopca, który ją zna, odwołać jego dotychczasowe zaręczyny
i zaręczyć z tą dziewczyną. Wtedy w zbiorze
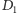 pojawia się dziewczyna
niezaręczona, którą można zaręczyć z
pojawia się dziewczyna
niezaręczona, którą można zaręczyć z
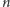 -tym chłopcem.
-tym chłopcem.
W przeciwnym razie kolejne zbiory
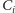 (chłopców zaręczonych
z dziewczynami z
(chłopców zaręczonych
z dziewczynami z
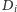 ) oraz
) oraz
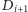 (dziewczyn, które znają
chłopców z
(dziewczyn, które znają
chłopców z
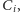 ale nie są z nimi zaręczone) możemy określać
podobnie. Jest jasne, że dla każdego
ale nie są z nimi zaręczone) możemy określać
podobnie. Jest jasne, że dla każdego
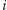 zbiory
zbiory
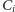 i
i
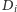 są
równoliczne. Jeśli dla pewnego
są
równoliczne. Jeśli dla pewnego
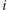 w zbiorze
w zbiorze
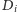 znajdzie się
niezaręczona dziewczyna, to zaczynając od niej, możemy utworzyć kaskadę.
Zrywamy zaręczyny chłopca z
znajdzie się
niezaręczona dziewczyna, to zaczynając od niej, możemy utworzyć kaskadę.
Zrywamy zaręczyny chłopca z
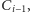 który ją zna, i z nim ją zaręczamy,
a jego dotychczasowa narzeczona z
który ją zna, i z nim ją zaręczamy,
a jego dotychczasowa narzeczona z
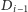 zostanie nową narzeczoną
chłopca z
zostanie nową narzeczoną
chłopca z
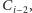 itd.
itd.
Jeśli nie możemy znaleźć niezaręczonej dziewczyny, to określamy
kolejne zbiory chłopców i dziewczyn, ale ten proces musi się zakończyć;
chłopców jest skończenie wielu, a więc dla pewnego
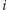 otrzymamy
otrzymamy
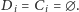 Wtedy nie możemy wszystkich chłopców wyswatać, ale to
oznacza, że istnieje zbiór chłopców
Wtedy nie możemy wszystkich chłopców wyswatać, ale to
oznacza, że istnieje zbiór chłopców
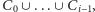 dla którego zbiór
znanych im dziewczyn
dla którego zbiór
znanych im dziewczyn
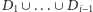 ma o przynajmniej jedną
dziewczynę mniej. No i już. Choć zapewne działalność prawdziwego biura
matrymonialnego jest znacznie bardziej skomplikowana.
ma o przynajmniej jedną
dziewczynę mniej. No i już. Choć zapewne działalność prawdziwego biura
matrymonialnego jest znacznie bardziej skomplikowana.