Mała Delta
Pizza Venna
Moja rodzina lubi pizzę, a ja lubię ją piec. Jednak w naszej gromadce nikt nie lubi jeść takiej samej pizzy, jak pozostali członkowie rodziny. Jest nas tylko czworo, więc można sobie z tym poradzić bez trudu, używając tylko dwóch składników – typowa pizza wygląda więc tak...
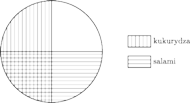
Rys. 1
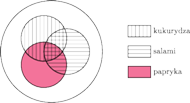
Rys. 2
Oczywiście, pomidory i ser są wszędzie, a dodatki za każdym razem inne. Tym sposobem bez zbytecznego trudu dostaję na jednym placku cztery gatunki pizzy i mogę zadowolić indywidualne upodobania nas wszystkich.
Co by jednak było, gdyby było nas więcej, powiedzmy ośmioro? Też żadna fatyga, każdy widział taki rysunek.
Układając go na blacie pizzy, można dostać 8 kombinacji smakowych, od Margherity (tylko ser i pomidory) na obrzeżu do wersji z wszystkimi trzema dodatkami w centrum.
A co dalej? Czy dałoby się w miarę regularnymi liniami ograniczyć złożone
z jednego kawałka obszary do położenia czterech dodatków tak, żeby te linie
dzieliły blat pizzy na 16 części i żeby każda z nich zawierała inną kombinację
dodatków? Albo, w końcu jesteśmy matematykami i nie tylko jedzenie nas
interesuje,
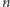 dodatków i
dodatków i
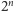 kombinacji?
kombinacji?
W tej ostatniej wersji pytanie jest już czysto matematyczne w swoim charakterze, a pierwszy je sformułował (i w tym samym artykule rozwiązał) John Venn w 1880 roku.
Ja wolę tu opisać trochę łatwiejsze do narysowania rozwiązanie Anthony’ego Edwardsa, które zostało opublikowane w późnych latach osiemdziesiątych ubiegłego wieku. Ma ono także tę zaletę, że chyba lepiej nadaje się do realizowania na powierzchni ciasta.
Zaczynamy tak jak na Rys. 1. W następnym kroku rysujemy okrąg współśrodkowy z brzegiem ciasta, który będzie granicą jednego z obszarów. (To daje nam alternatywne rozwiązanie problemu 8 smaków.

Rys. 3
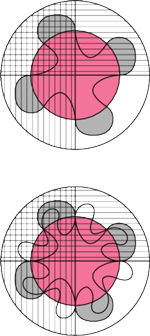
Rys. 4
W tym momencie każdy ze smaków ma fragment swojej granicy przebiegający wzdłuż małego okręgu. To bardzo ważna własność naszego rysunku – będziemy ją zachowywać mimo zwiększającej się liczby obszarów i smaków. Następna granica wije się wokół wewnętrznego okręgu, odcinając kawałek od każdego smaku. Jeszcze następna jest podobna do poprzedniej, tylko jest dwa razy bardziej kręta (na ostatnim rysunku obszar przez nią ograniczony nie został już pokolorowany).
Dalsze kroki konstrukcji każdy może sobie łatwo wyobrazić.
Pozostaje tylko pytanie, po co matematycy interesowali się problemem dotyczącym pizzy? Okazuje się jednak, że diagramy Venna (bo tak się one nazywają) mają całkiem matematyczne zastosowania. Oto jedno z nich, które tutaj podajemy „na wiarę”. Może Czytelnicy się zastanowią, dlaczego tak jest:
Twierdzenie. Dla każdych czterech zbiorów
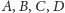 zachodzi
równość
zachodzi
równość

Wskazówka: Narysować zbiory opisane wyrażeniami po lewej i po prawej
stronie znaku równości na diagramie Venna. Jeśli okażą się równe, to
równość będzie zachodziła dla dowolnych zbiorów
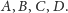 W przeciwnym razie od razu stanowią kontrprzykład.
W przeciwnym razie od razu stanowią kontrprzykład.
Ten artykuł został przygotowany na podstawie artykułu Franka Ruskey’a w The Electronic Journal of Combinatorics. Gorąco polecam jego lekturę, a przede wszystkim podziwianie pięknych, animowanych ilustracji na tej stronie.