Co to jest?
Miara liczności
Jednym z podstawowych sposobów mierzenia zbioru jest liczenie jego
elementów. Liczenie ma jednak jasny sens tylko dla zbiorów skończonych.
Wiadomo, co to znaczy, że jakiś zbiór ma
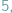
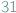 czy
czy
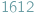 elementów. W przypadku zbiorów nieskończonych sytuacja jest natomiast
znacznie mniej oczywista. Czy zbiorowi nieskończonemu da się w ogóle
przypisać liczbę elementów sensowniej niż przez uznanie, że wynosi ona
zawsze
elementów. W przypadku zbiorów nieskończonych sytuacja jest natomiast
znacznie mniej oczywista. Czy zbiorowi nieskończonemu da się w ogóle
przypisać liczbę elementów sensowniej niż przez uznanie, że wynosi ona
zawsze
 ?
?
Punktem wyjścia do poszukiwania odpowiedzi jest następująca obserwacja:
zbiory
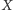 i
i
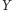 można uznać za równoliczne, jeśli istnieje
bijekcja
można uznać za równoliczne, jeśli istnieje
bijekcja
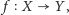 czyli taka różnowartościowa funkcja z
czyli taka różnowartościowa funkcja z
 w
w
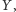 której zbiorem wartości jest całe
której zbiorem wartości jest całe
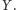 Okazuje się, że jest to
bardzo trafna definicja równoliczności, mimo że w zastosowaniu do
zbiorów nieskończonych prowadzi do zaskakujących wniosków. Zbiór
nieskończony może być, między innymi, równoliczny ze swoim
właściwym podzbiorem: przykładowo, zbiory
Okazuje się, że jest to
bardzo trafna definicja równoliczności, mimo że w zastosowaniu do
zbiorów nieskończonych prowadzi do zaskakujących wniosków. Zbiór
nieskończony może być, między innymi, równoliczny ze swoim
właściwym podzbiorem: przykładowo, zbiory
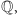
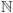 i
i
 są
równoliczne (
są
równoliczne (
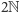 oznacza zbiór liczb parzystych).
oznacza zbiór liczb parzystych).
Gdy dwa zbiory skończone są równoliczne, to jest tak dlatego, iż istnieje taka
liczba naturalna
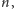 że oba zbiory mają po
że oba zbiory mają po
 elementów.
Chcielibyśmy również zbiorom nieskończonym przyporządkować takie
kanoniczne obiekty, które wskazywałyby na to, że dany zbiór należy do danej
klasy równoliczności. Okazuje się, że nasz cel da się zrealizować:
z każdym zbiorem
elementów.
Chcielibyśmy również zbiorom nieskończonym przyporządkować takie
kanoniczne obiekty, które wskazywałyby na to, że dany zbiór należy do danej
klasy równoliczności. Okazuje się, że nasz cel da się zrealizować:
z każdym zbiorem
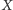 można związać pewien zbiór
można związać pewien zbiór
 równoliczny z
równoliczny z
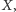 w taki sposób, że
w taki sposób, że
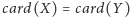 dokładnie wtedy, gdy
dokładnie wtedy, gdy
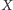 i
i
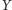 są równoliczne. Dla
są równoliczne. Dla
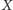 skończonego
skończonego
 -elementowego
-elementowego
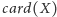 jest po prostu liczbą
naturalną
jest po prostu liczbą
naturalną
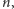 identyfikowaną ze zbiorem
identyfikowaną ze zbiorem
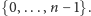 Zbiór
Zbiór
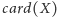 nazywamy mocą zbioru
nazywamy mocą zbioru
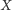 (a czasem liczbą
elementów
(a czasem liczbą
elementów
 ), a wszystkie możliwe moce nazywamy liczbami
kardynalnymi. Liczby kardynalne oznaczamy najczęściej literami
), a wszystkie możliwe moce nazywamy liczbami
kardynalnymi. Liczby kardynalne oznaczamy najczęściej literami
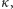
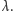
Definicja.
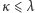 wtedy i tylko wtedy, gdy istnieje funkcja
różnowartościowa
wtedy i tylko wtedy, gdy istnieje funkcja
różnowartościowa
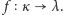
Zatem,
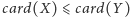 dokładnie wtedy, gdy
dokładnie wtedy, gdy
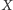 jest
równoliczny z podzbiorem
jest
równoliczny z podzbiorem
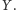 Zachodzi oczekiwane, ale bardzo ważne
twierdzenie
Zachodzi oczekiwane, ale bardzo ważne
twierdzenie
Twierdzenie (Cantora–Bernsteina). Jeśli
 i
i
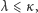 to
to
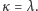
Możemy więc przyjąć:
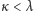 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
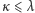 i
i
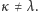
Czytelnik bez wątpienia zauważył, że nie podaliśmy definicji
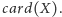 Było to zaniedbanie celowe: zdefiniowanie liczb kardynalnych, a zwłaszcza
wyjaśnienie sensu definicji, to proces dość żmudny. Z naszego punktu
widzenia ważniejsza od dokładnej definicji jest zresztą struktura liczb
kardynalnych. Okazuje się na przykład, że dla dowolnych zbiorów
Było to zaniedbanie celowe: zdefiniowanie liczb kardynalnych, a zwłaszcza
wyjaśnienie sensu definicji, to proces dość żmudny. Z naszego punktu
widzenia ważniejsza od dokładnej definicji jest zresztą struktura liczb
kardynalnych. Okazuje się na przykład, że dla dowolnych zbiorów
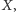
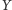 zachodzi
zachodzi
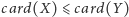 lub
lub
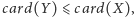 a ponadto w każdym niepustym zbiorze liczb kardynalnych istnieje
najmniejsza. Największej liczby kardynalnej nie ma, o czym się wkrótce
przekonamy. Najmniejszymi są liczby kardynalne skończone, czyli po prostu
liczby naturalne. Najmniejszą liczbą nieskończoną jest moc zbioru liczb
naturalnych, oznaczana symbolem
a ponadto w każdym niepustym zbiorze liczb kardynalnych istnieje
najmniejsza. Największej liczby kardynalnej nie ma, o czym się wkrótce
przekonamy. Najmniejszymi są liczby kardynalne skończone, czyli po prostu
liczby naturalne. Najmniejszą liczbą nieskończoną jest moc zbioru liczb
naturalnych, oznaczana symbolem
 Zbiory równoliczne z
Zbiory równoliczne z
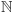 nazywamy przeliczalnymi. Następną po
nazywamy przeliczalnymi. Następną po
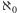 liczbą kardynalną jest…ale
o tym za chwilę.
liczbą kardynalną jest…ale
o tym za chwilę.
Na liczbach kardynalnych można wykonywać niektóre szkolne działania
arytmetyczne: dodawanie, mnożenie, potęgowanie. Jeśli
 i
i
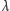 są
liczbami kardynalnymi, to
są
liczbami kardynalnymi, to
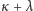 jest mocą sumy dwu rozłącznych
zbiorów, z których jeden ma moc
jest mocą sumy dwu rozłącznych
zbiorów, z których jeden ma moc
 a drugi
a drugi
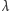 ;
;
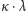 jest
mocą iloczynu kartezjańskiego zbioru mocy
jest
mocą iloczynu kartezjańskiego zbioru mocy
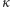 i zbioru mocy
i zbioru mocy
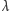 ;
wreszcie
;
wreszcie
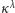 jest mocą zbioru wszystkich funkcji ze zbioru mocy
jest mocą zbioru wszystkich funkcji ze zbioru mocy
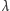 w zbiór mocy
w zbiór mocy
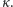 W szczególności,
W szczególności,
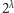 jest mocą zbioru
wszystkich podzbiorów zbioru mocy
jest mocą zbioru
wszystkich podzbiorów zbioru mocy
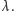
Dodawanie i mnożenie liczb nieskończonych to wyjątkowo proste
operacje. Jeśli choć jedna z liczb
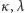 jest nieskończona, to
jest nieskończona, to
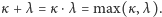 Pokażmy dla przykładu, że
Pokażmy dla przykładu, że
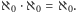 Jeśli
Jeśli
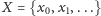 i
i
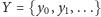 są zbiorami przeliczalnymi, to
funkcja
są zbiorami przeliczalnymi, to
funkcja
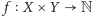 zadana wzorem
zadana wzorem
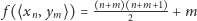 jest bijekcją między
jest bijekcją między
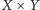 a
a
 Czytelnik być może zechce nie
tylko uzupełnić szczegóły tego rozumowania, ale i zastanowić się nad
„geometrycznym sensem” funkcji
Czytelnik być może zechce nie
tylko uzupełnić szczegóły tego rozumowania, ale i zastanowić się nad
„geometrycznym sensem” funkcji
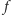 (chodzi o ponumerowanie liczbami
naturalnymi macierzy o przeliczalnie wielu wierszach, z których każdy jest
przeliczalny).
(chodzi o ponumerowanie liczbami
naturalnymi macierzy o przeliczalnie wielu wierszach, z których każdy jest
przeliczalny).
Z potęgowaniem liczb kardynalnych nie jest już tak prosto. Udowodnimy, że
już
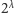 musi być zawsze ostro większe od
musi być zawsze ostro większe od
 Dowód
Dowód
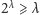 jest łatwy, wystarczy zatem sprawdzić, że żaden zbiór
jest łatwy, wystarczy zatem sprawdzić, że żaden zbiór
 nie
może być równoliczny ze zbiorem wszystkich podzbiorów
nie
może być równoliczny ze zbiorem wszystkich podzbiorów
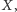 oznaczanym przez
oznaczanym przez
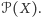 Przypuśćmy, że
Przypuśćmy, że
 jest
bijekcją i rozważmy zbiór
jest
bijekcją i rozważmy zbiór
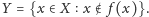 Oczywiście
Oczywiście
 a zatem istnieje taki
a zatem istnieje taki
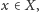 że
że
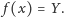 Zapytajmy teraz, czy
Zapytajmy teraz, czy
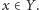 Chwila zastanowienia pozwala stwierdzić, że
każda z dwu możliwych odpowiedzi prowadzi do sprzeczności.
Chwila zastanowienia pozwala stwierdzić, że
każda z dwu możliwych odpowiedzi prowadzi do sprzeczności.
Tak więc, funkcja wykładnicza
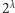 zawsze zwiększa swój argument. Dalej
jednak sprawy stają się bardziej zagmatwane. Oznaczmy następną po
zawsze zwiększa swój argument. Dalej
jednak sprawy stają się bardziej zagmatwane. Oznaczmy następną po
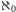 liczbę kardynalną przez
liczbę kardynalną przez
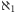 i zadajmy naturalne pytanie: czy
i zadajmy naturalne pytanie: czy
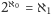 ? Pozytywna odpowiedź, w którą wierzył Cantor, nazywa się
hipotezą continuum,
? Pozytywna odpowiedź, w którą wierzył Cantor, nazywa się
hipotezą continuum,
 („continuum” bywa czasem określeniem zbioru
liczb rzeczywistych, a
(„continuum” bywa czasem określeniem zbioru
liczb rzeczywistych, a
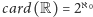 ). Problem rozstrzygnięcia hipotezy
continuum był pierwszy na słynnej liście problemów otwartych przedstawionej
przez Hilberta na Międzynarodowym Kongresie Matematyków w 1900
r.
). Problem rozstrzygnięcia hipotezy
continuum był pierwszy na słynnej liście problemów otwartych przedstawionej
przez Hilberta na Międzynarodowym Kongresie Matematyków w 1900
r.
A zatem: czy
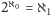 ? W 1938 r. Kurt Gödel pokazał, że przy założeniu
niesprzeczności zwykłych aksjomatów teorii mnogości niesprzeczna z nimi
jest nie tylko
? W 1938 r. Kurt Gödel pokazał, że przy założeniu
niesprzeczności zwykłych aksjomatów teorii mnogości niesprzeczna z nimi
jest nie tylko
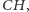 ale nawet tak zwana uogólniona hipoteza continuum,
ale nawet tak zwana uogólniona hipoteza continuum,
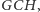 czyli zdanie mówiące, że dla każdej nieskończonej
czyli zdanie mówiące, że dla każdej nieskończonej

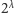 jest następną liczbą po
jest następną liczbą po
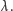 Metoda Gödla polegała na wybraniu
z uniwersum wszystkich zbiorów „tylko tych, których istnienie jest
wymuszone przez aksjomaty” (tzw. zbiorów konstruowalnych) i pokazaniu, że
w tak ograniczonej strukturze
Metoda Gödla polegała na wybraniu
z uniwersum wszystkich zbiorów „tylko tych, których istnienie jest
wymuszone przez aksjomaty” (tzw. zbiorów konstruowalnych) i pokazaniu, że
w tak ograniczonej strukturze
 jest spełniona. W 1963 r.
natomiast Paul Cohen wprowadził tzw. metodę forcingu (która dla odmiany
polega na dodawaniu nowych elementów do istniejących struktur) i za jej
pomocą udowodnił, że również negacja
jest spełniona. W 1963 r.
natomiast Paul Cohen wprowadził tzw. metodę forcingu (która dla odmiany
polega na dodawaniu nowych elementów do istniejących struktur) i za jej
pomocą udowodnił, że również negacja
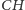 jest niesprzeczna
z aksjomatami.
jest niesprzeczna
z aksjomatami.
Hipoteza continuum jest więc nierozstrzygalna: nie da się jej ani udowodnić,
ani obalić w oparciu o standardowo przyjmowane aksjomaty. Interpretacja tego
rezultatu jest sporna. Dla jednych zamyka on problem, a może świadczy
nawet o tym, że
 jest pozbawiona wartości logicznej czy
„z przyczyn zasadniczych niejasna”. Dla innych
jest pozbawiona wartości logicznej czy
„z przyczyn zasadniczych niejasna”. Dla innych
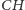 pozostaje
wartym badania problemem, rodzącym m. in. pytania o ewentualne nowe
aksjomaty.
pozostaje
wartym badania problemem, rodzącym m. in. pytania o ewentualne nowe
aksjomaty.
Tak czy inaczej, wynik Cohena zamknął pewną epokę w dziejach teorii liczb kardynalnych: podstawy pojęciowe teorii były już dawno ustalone, a jej najsłynniejszy problem otwarty okazał się nierozstrzygalny. Z drugiej jednak strony, stworzone przez Cohena metody spowodowały bujny rozwój teorii mnogości, umożliwiając rozwiązanie wielu klasycznych problemów oraz postawienie (i rozwiązanie) wielu nowych. Na zakończenie wspomnijmy więc pokrótce o dwu kierunkach badań, które odegrały znaczącą rolę w ostatnich kilku dziesięcioleciach.
Skoro wiadomo już było, jaki jest status
 ważne stawało się
ogólne pytanie o możliwe zachowanie funkcji
ważne stawało się
ogólne pytanie o możliwe zachowanie funkcji
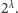 Dość szybko
odkryto, że dla „typowych” liczb kardynalnych (w tym dla wszystkich liczb
nieskończonych, które są bezpośrednimi następnikami innych liczb)
dowolność jest prawie całkowita. W. Easton udowodnił w 1970 r., że dla
takich liczb dowolny przebieg funkcji wykładniczej zgodny z dwoma
elementarnymi warunkami (funkcja
Dość szybko
odkryto, że dla „typowych” liczb kardynalnych (w tym dla wszystkich liczb
nieskończonych, które są bezpośrednimi następnikami innych liczb)
dowolność jest prawie całkowita. W. Easton udowodnił w 1970 r., że dla
takich liczb dowolny przebieg funkcji wykładniczej zgodny z dwoma
elementarnymi warunkami (funkcja
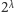 musi być niemalejąca i spełniać
pewne wzmocnienie warunku
musi być niemalejąca i spełniać
pewne wzmocnienie warunku
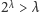 ) jest niesprzeczny z aksjomatami.
W szczególności, na nieskończonych argumentach funkcja wykładnicza nie
musi być ściśle rosnąca. Dla „nietypowych” liczb (tzw. singularnych)
dowolność przebiegu funkcji wykładniczej jest znacznie mniejsza. Tu badania
trwały dużo dłużej i nie przyniosły eleganckiego ogólnego wyniku w rodzaju
twierdzenia Eastona.
) jest niesprzeczny z aksjomatami.
W szczególności, na nieskończonych argumentach funkcja wykładnicza nie
musi być ściśle rosnąca. Dla „nietypowych” liczb (tzw. singularnych)
dowolność przebiegu funkcji wykładniczej jest znacznie mniejsza. Tu badania
trwały dużo dłużej i nie przyniosły eleganckiego ogólnego wyniku w rodzaju
twierdzenia Eastona.
Inny ważny przedmiot badań to tzw. duże liczby kardynalne. Mówiąc
w uproszczeniu, duża liczba to taka, która ma pewne własności
kombinatoryczne sprawiające, że musi być „znacznie większa” od liczb ją
poprzedzających (mniej więcej w takim sensie, w jakim liczba
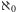 jest
znacznie większa od wszystkich liczb skończonych). Przykładem stosunkowo
małych dużych liczb kardynalnych są liczby nieosiągalne, tj. takie
jest
znacznie większa od wszystkich liczb skończonych). Przykładem stosunkowo
małych dużych liczb kardynalnych są liczby nieosiągalne, tj. takie
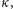 że
ilekroć
że
ilekroć
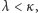 to również
to również
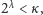 a ponadto żaden zbiór mocy
a ponadto żaden zbiór mocy
 nie jest sumą mniej niż
nie jest sumą mniej niż
 zbiorów mocy mniejszej niż
zbiorów mocy mniejszej niż
Duże liczby kardynalne mają dość specyficzny status logiczny. Można pokazać, że ich nieistnienie jest niesprzeczne ze zwykłymi aksjomatami teorii mnogości, oczywiście zakładając niesprzeczność samych aksjomatów. Domniemujemy, że istnienie dużych liczb kardynalnych jest również niesprzeczne z aksjomatami, ale tego dla odmiany nie można udowodnić – w przeciwnym przypadku popadlibyśmy w sprzeczność z drugim twierdzeniem Gödla. Mimo to wielu badaczy zajmujących się teorią mnogości ma dość przychylny stosunek do aksjomatów o istnieniu dużych liczb. Co więcej, aksjomaty takie bywają wykorzystywane i w głównonurtowej matematyce (np. w geometrii algebraicznej i topologii algebraicznej używa się czasem liczb nieosiągalnych w postaci tzw. uniwersów Grothendiecka). Niewykluczone, że któreś z tych aksjomatów zostaną kiedyś powszechnie przyjęte, choć na pewno nie odbędzie się to bez kontrowersji.