MiNI Matematyka»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu MiNI Matematyka
- Publikacja w Delcie: grudzień 2015
- Publikacja elektroniczna: 30-11-2015
Niech 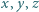 będą liczbami rzeczywistymi dodatnimi. Udowodnić, że
będą liczbami rzeczywistymi dodatnimi. Udowodnić, że

Niech 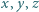 będą liczbami rzeczywistymi dodatnimi. Udowodnić, że
będą liczbami rzeczywistymi dodatnimi. Udowodnić, że

Niech 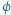 będzie funkcją różnowartościową odwzorowującą zbiór liczb całkowitych dodatnich w siebie. Wykazać, że dla każdej liczby całkowitej dodatniej
będzie funkcją różnowartościową odwzorowującą zbiór liczb całkowitych dodatnich w siebie. Wykazać, że dla każdej liczby całkowitej dodatniej 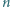 zachodzi nierówność
zachodzi nierówność
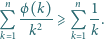
Udowodnić, że dla dodatnich liczb 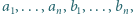 spełniających
spełniających 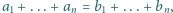 prawdziwa jest nierówność
prawdziwa jest nierówność
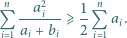
Niech 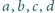 będą takimi liczbami rzeczywistymi, że
będą takimi liczbami rzeczywistymi, że

Wykazać, że 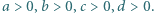
Liczby rzeczywiste 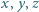 spełniają warunki
spełniają warunki

Udowodnić, że 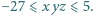
Zadanie 704 zaproponował pan Paweł Kubit z Krakowa.
Wyznaczyć największą liczbę 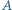 oraz najmniejszą liczbę
oraz najmniejszą liczbę 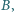 takie że dla każdej czwórki liczb rzeczywistych
takie że dla każdej czwórki liczb rzeczywistych 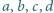 spełniona jest nierówność
spełniona jest nierówność
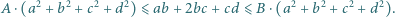
Niech 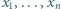 będą liczbami rzeczywistymi dodatnimi, przy czym
będą liczbami rzeczywistymi dodatnimi, przy czym 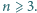 Dla wygody przyjmijmy dodatkowo, że
Dla wygody przyjmijmy dodatkowo, że 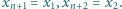 Udowodnić, że
Udowodnić, że
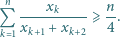
Udowodnić, że dla nieujemnych liczb 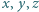 prawdziwa jest nierówność
prawdziwa jest nierówność
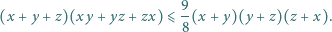
Dane są dodatnie liczby całkowite 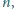
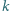 oraz takie nieujemne liczby rzeczywiste
oraz takie nieujemne liczby rzeczywiste 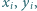 że
że 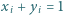 dla każdego
dla każdego 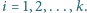 Wykaż, że zachodzi nierówność
Wykaż, że zachodzi nierówność

Wykaż, że dla dowolnej liczby rzeczywistej 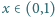 oraz dowolnych dodatnich liczb całkowitych
oraz dowolnych dodatnich liczb całkowitych 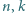 zachodzi nierówność
zachodzi nierówność

Udowodnić, że dla każdej liczby naturalnej 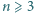 prawdziwa jest nierówność
prawdziwa jest nierówność
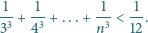
Niech  oznacza sumę cyfr liczby całkowitej
oznacza sumę cyfr liczby całkowitej 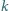 w zapisie dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb całkowitych
w zapisie dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb całkowitych 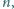 że
że 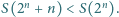
Dane są takie liczby całkowite 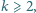
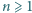 oraz
oraz 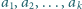 i
i 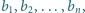 że
że 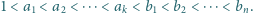 Wykazać, że jeżeli
Wykazać, że jeżeli 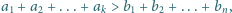 to
to 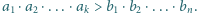
Niech liczby 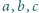 z przedziału
z przedziału 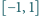 spełniają
spełniają
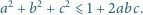
Pokazać, że dla każdej liczby całkowitej 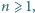
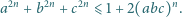
Określmy funkcję 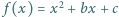 dla pewnych liczb rzeczywistych
dla pewnych liczb rzeczywistych 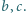 Wiadomo, że zbiór
Wiadomo, że zbiór 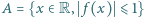 jest zbiorem pustym, odcinkiem lub sumą dwóch odcinków (w zależności od wartości
jest zbiorem pustym, odcinkiem lub sumą dwóch odcinków (w zależności od wartości 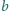 i
i  ). Udowodnić, że za każdym razem łączna długość nie przekracza
). Udowodnić, że za każdym razem łączna długość nie przekracza 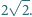
Niech
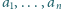 będą liczbami dodatnimi i niech
będą liczbami dodatnimi i niech
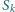 oznacza sumę
wszystkich iloczynów różnych
oznacza sumę
wszystkich iloczynów różnych
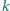 liczb spośród
liczb spośród
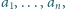
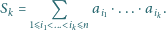
Udowodnić, że dla każdego naturalnego
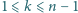 spełniona jest
nierówność
spełniona jest
nierówność
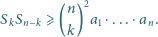
Zadanie 682 zaproponował pan Paweł Najman z Krakowa.
Liczby dodatnie 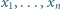 spełniają warunek
spełniają warunek
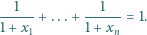
Udowodnić, że
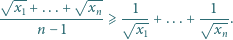
Udowodnić, że dla dodatnich liczb całkowitych
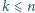 prawdziwa jest
nierówność
prawdziwa jest
nierówność
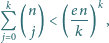
gdzie
 to stała zdefiniowana np. jako
to stała zdefiniowana np. jako
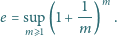
Rozważamy trójki liczb rzeczywistych
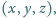 spełniające
warunki
spełniające
warunki
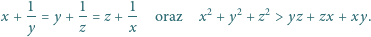 |
Wyznaczyć wszystkie możliwe wartości iloczynu