Zadanie ZM-1602
o zadaniu...
- Publikacja w Delcie: maj 2019
- Publikacja elektroniczna: 30 kwietnia 2019
Odcinki 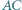 i
i 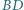 przecinają się w punkcie
przecinają się w punkcie 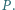 Wykazać, że
Wykazać, że
![√ --------- √ ------- √ ------- [ABCD] ⩾ [ABP + [CDP ,](/math/temat/matematyka/geometria/planimetria/zadania/2019/04/30/zm-1602/4x-6f30022e90be6b8372c582cf70ce78e46db1ae4d-dm-2C,6B,73-FF,FF,FF.gif)
gdzie ![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/04/30/zm-1602/5x-6f30022e90be6b8372c582cf70ce78e46db1ae4d-im-2C,6B,73-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 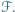
Odcinki 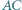 i
i 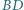 przecinają się w punkcie
przecinają się w punkcie 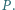 Wykazać, że
Wykazać, że
![√ --------- √ ------- √ ------- [ABCD] ⩾ [ABP + [CDP ,](/math/temat/matematyka/geometria/planimetria/zadania/2019/04/30/zm-1602/4x-6f30022e90be6b8372c582cf70ce78e46db1ae4d-dm-2C,6B,73-FF,FF,FF.gif)
gdzie ![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/04/30/zm-1602/5x-6f30022e90be6b8372c582cf70ce78e46db1ae4d-im-2C,6B,73-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 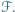
Dla ustalonych liczb rzeczywistych 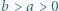 oraz parzystej liczby naturalnej
oraz parzystej liczby naturalnej 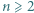 wyznaczyć kres górny wartości stosunku
wyznaczyć kres górny wartości stosunku 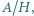 gdzie
gdzie 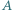 i
i 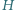 to (odpowiednio) średnia arytmetyczna i średnia harmoniczna
to (odpowiednio) średnia arytmetyczna i średnia harmoniczna 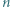 liczb wybranych dowolnie z przedziału
liczb wybranych dowolnie z przedziału ![[a,b].](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/7x-ef372a8dfa93edadbc34939244d39cca0f9e4c26-im-2C,6B,73-FF,FF,FF.gif)
Udowodnić, że dla liczb dodatnich 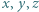 prawdziwa jest nierówność
prawdziwa jest nierówność

Wyznaczyć najmniejszą oraz największą wartość wyrażenia

dla liczb rzeczywistych  i
i 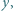 niebędących jednocześnie zerami.
niebędących jednocześnie zerami.
Udowodnić, że dla liczb rzeczywistych 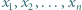 zachodzi nierówność
zachodzi nierówność

Wykazać nierówność pomiędzy średnią arytmetyczną i kwadratową

dla liczb rzeczywistych 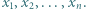
Suma liczb dodatnich 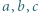 jest równa
jest równa 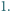 Udowodnić, że
Udowodnić, że

Liczby dodatnie 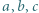 spełniają równość
spełniają równość 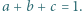 Wykazać, że
Wykazać, że

Udowodnić, że dla liczb nieujemnych 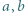 i
i  zachodzi nierówność
zachodzi nierówność

Niech 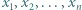 będą liczbami dodatnimi. Przyjmijmy
będą liczbami dodatnimi. Przyjmijmy 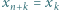 dla całkowitych
dla całkowitych 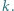 Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
Dowieść, że prawdziwa jest co najmniej jedna z nierówności:

Wykazać, że dla liczb rzeczywistych 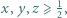 spełniających warunek
spełniających warunek 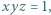 zachodzi nierówność
zachodzi nierówność

Dowieść, że liczby rzeczywiste 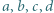 spełniają nierówność
spełniają nierówność

Dowieść, że dla liczb rzeczywistych 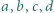 zachodzi nierówność
zachodzi nierówność

Liczby ![x ,x ,...,x ∈ [−1,1] 1 2 n](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-19_05-kpm-12/1x-e242253ed078688e97a06aead3aec19a78e70a97-im-2C,6B,73-FF,FF,FF.gif) spełniają warunek
spełniają warunek 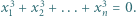 Dowieść, że
Dowieść, że

Udowodnić, że dla liczb dodatnich 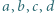 zachodzi nierówność
zachodzi nierówność

Nana jest dodatnia liczba całkowita 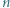 o tej własności, że
o tej własności, że 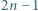 jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych
jest liczbą pierwszą. Wykazać, że w zbiorze dowolnych 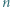 różnych dodatnich liczb całkowitych można wskazać takie dwie liczby
różnych dodatnich liczb całkowitych można wskazać takie dwie liczby 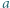 i
i 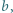 że
że

Dana jest dodatnia liczba całkowita 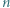 o tej własności, że
o tej własności, że 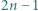 jest liczbą złożoną. Skonstruować zbiór
jest liczbą złożoną. Skonstruować zbiór 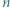 różnych dodatnich liczb całkowitych o tej własności, że dla każdych dwóch elementów tego zbioru
różnych dodatnich liczb całkowitych o tej własności, że dla każdych dwóch elementów tego zbioru 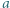 i
i 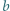 zachodzi nierówność
zachodzi nierówność

Udowodnić nierówność Schura
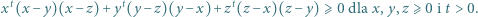
Wyznaczyć największą możliwą wartość wyrażenia 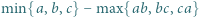 dla liczb rzeczywistych
dla liczb rzeczywistych 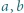 i
i 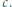
Liczby rzeczywiste 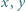 i
i  spełniają warunki:
spełniają warunki:

Dowieść, że jedna z nich jest równa sumie pozostałych