Zadanie ZM-1412
o zadaniu...
- Publikacja w Delcie: luty 2014
- Publikacja elektroniczna: 31-01-2014
Dane są liczby rzeczywiste
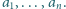 Niech
Niech
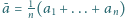 oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
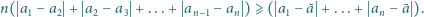 |
Dane są liczby rzeczywiste
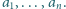 Niech
Niech
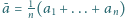 oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
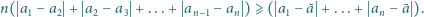 |
Udowodnić, że dowolna liczba rzeczywista
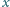 spełnia nierówność
spełnia nierówność
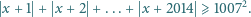 |
Zadanie 670 zaproponował pan Paweł Kubit z Krakowa.
Udowodnić nierówność
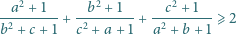
dla liczb rzeczywistych
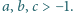
Udowodnić, że dla malejącego ciągu
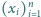 liczb rzeczywistych
dodatnich prawdziwa jest nierówność
liczb rzeczywistych
dodatnich prawdziwa jest nierówność
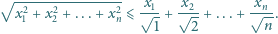 |
Udowodnić, że dla
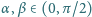 prawdziwa jest nierówność
prawdziwa jest nierówność
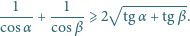 |
Kiedy zachodzi równość?
Udowodnić, że istnieje liczba
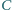 o następującej własności: jeśli
równanie
o następującej własności: jeśli
równanie
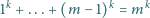
ma rozwiązanie dla pewnych liczb naturalnych
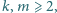 to
to
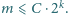
Udowodnić, że dla liczb rzeczywistych
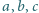 jest spełniona
nierówność
jest spełniona
nierówność
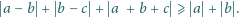
Dana jest liczba naturalna
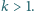 Znaleźć wszystkie liczby naturalne
Znaleźć wszystkie liczby naturalne
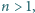 spełniające nierówność
spełniające nierówność

gdzie
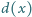 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej

Niech funkcja
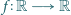 będzie ograniczona z góry, tzn. istnieje taka
liczba
będzie ograniczona z góry, tzn. istnieje taka
liczba
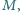 że
że
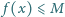 dla każdego
dla każdego
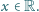 Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
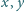 spełniona jest
nierówność
spełniona jest
nierówność
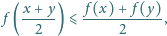
to
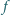 jest funkcją stałą.
jest funkcją stałą.
W szczególności, funkcje wypukłe nie są ograniczone z góry, chyba że są stałe.
Wykazać, że jeśli każda z liczb
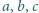 jest nie mniejsza od
jest nie mniejsza od
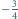 oraz
oraz
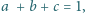 to
to

Zadanie 506 z Klubu 44M
Udowodnić, że dla dowolnych liczb dodatnich
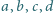 zachodzi
nierówność
zachodzi
nierówność

Udowodnić, że dla dowolnych liczb dodatnich
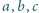 zachodzi
nierówność
zachodzi
nierówność

Zwardoń 2006
Liczby rzeczywiste
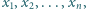 gdzie
gdzie
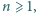 spełniają warunki
spełniają warunki

Udowodnić, że
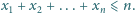
Jugosławia 1986
Udowodnić, że dla dowolnych liczb dodatnich
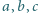 zachodzi
nierówność
zachodzi
nierówność

Japonia 1997
Udowodnić, że dla dowolnych liczb dodatnich
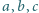 zachodzi
nierówność
zachodzi
nierówność

Zadanie 652 zaproponował pan Witold Bednarek z Łodzi.
Udowodnić nierówność
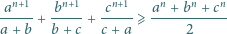
dla liczb rzeczywistych
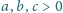 oraz liczb całkowitych
oraz liczb całkowitych
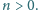
Liczby rzeczywiste
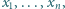 które są nie mniejsze niż
które są nie mniejsze niż
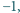 spełniają
równość
spełniają
równość
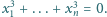 Udowodnić, że
Udowodnić, że
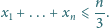
Udowodnić, że dla różnych liczb dodatnich
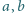 i liczby całkowitej
dodatniej
i liczby całkowitej
dodatniej
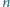 zachodzi nierówność
zachodzi nierówność
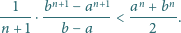
Wykazać, że nie istnieje funkcja
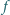 przekształcająca zbiór liczb
dodatnich w siebie, spełniająca dla wszystkich dodatnich
przekształcająca zbiór liczb
dodatnich w siebie, spełniająca dla wszystkich dodatnich
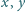 nierówność
nierówność
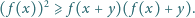
Niech
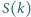 oznacza sumę cyfr liczby całkowitej
oznacza sumę cyfr liczby całkowitej
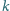 w zapisie
dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb
całkowitych
w zapisie
dziesiętnym. Dowieść, że istnieje nieskończenie wiele takich dodatnich liczb
całkowitych
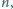 że
że
