Wielomiany, nierówności i Newton
Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...
Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...
Algebra Kącik początkującego olimpijczyka
Standardowym postępowaniem jest ujednorodnianie dowodzonych nierówności za pomocą danego w zadaniu warunku. Ciekawiej jest na odwrót - gdy mamy udowodnić jednorodną nierówność, możemy często założyć coś dodatkowo o występującej w niej zmiennych. Naprawdę!
Zacznijmy od przypomnienia zadania 766 z Klubu 44M (Delta 9/2018)...
Analiza Kącik początkującego olimpijczyka
Kwadrat liczby rzeczywistej jest nieujemny (fanfary!).
Algebra Kącik początkującego olimpijczyka
O wyrażeniach symetrycznych oraz uproszczeniach, które można stosować w rozwiązywaniu zadań z takimi wyrażeniami.
Teoria liczb Kącik początkującego olimpijczyka
Nieoczywiste zastosowania oczywistego stwierdzenia: pomiędzy dwiema kolejnymi liczbami całkowitymi nie ma żadnej liczby całkowitej.
Praca nadesłana na Konkurs Prac Uczniowskich dotyczy nowej metody dowodzenia pewnych nierówności. W niniejszym skrócie umieszczam jedynie ważniejsze twierdzenia (bez dowodów) i niektóre ich zastosowania.
Nierówności między średnimi, a w szczególności nierówność między średnią arytmetyczną i geometryczną (oznaczana dalej A-G), to jedne z podstawowych narzędzi dowodowych w arsenale każdego olimpijczyka...
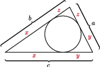
Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków 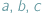 pewnego trójkąta, często przydaje się podstawienie Raviego:
pewnego trójkąta, często przydaje się podstawienie Raviego: 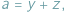
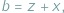
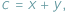 gdzie
gdzie 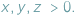 Takie liczby
Takie liczby 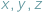 zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.
zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.
W dowodzeniu nierówności często pomocna bywa tak zwana metoda stycznych. Zdarza się, że wykres funkcji leży nad pewną prostą styczną do niego lub pod taką prostą (wszędzie lub tylko na jakimś przedziale). To oznacza, że możemy oszacować wartości tej funkcji przez wartości funkcji liniowej, której wykresem jest wybrana styczna. Żeby takie oszacowanie doprowadziło do celu, wybrana styczna musi przechodzić przez punkt, dla którego badana nierówność jest równością. Przyjrzymy się kilku przykładom zastosowań tej metody.

Gdy poznajemy matematykę, liczby oznaczane symbolami
 oraz
oraz
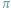 pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
 jest liczbą niewymierną (L. Euler, 1737 r.) oraz
jest liczbą niewymierną (L. Euler, 1737 r.) oraz
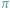 jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
 wykazał
Ch. Hermite w 1873 r., a przestępność liczby
wykazał
Ch. Hermite w 1873 r., a przestępność liczby
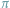 wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.
wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.
Analiza Stowarzyszenie na rzecz Edukacji Matematycznej