Klub 44M - zadania XI 2020»Zadanie 809
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2020
- Publikacja w Delcie: listopad 2020
- Publikacja elektroniczna: 1 listopada 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (364 KB)
W trójkącie ostrokątnym 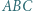 wysokości
wysokości 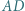 i
i 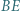 przecinają się w punkcie
przecinają się w punkcie 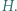 Proste
Proste 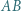 i
i 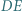 przecinają się w punkcie
przecinają się w punkcie 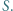 Prosta przechodząca przez środek
Prosta przechodząca przez środek 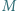 boku
boku 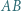 i równoległa do dwusiecznej kąta
i równoległa do dwusiecznej kąta 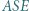 przecina proste
przecina proste 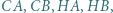 odpowiednio, w punktach
odpowiednio, w punktach 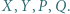 Udowodnić, że okręgi opisane na trójkątach
Udowodnić, że okręgi opisane na trójkątach 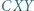 i
i 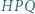 są przystające.
są przystające.
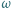

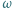
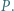
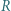
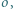
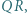
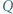
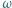
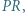

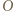
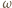
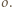
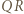
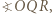
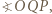
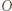
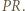
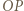
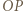
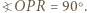
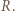
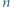 -kąta
-kąta 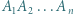 leży taki punkt
leży taki punkt 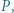 że każdy z trójkątów
że każdy z trójkątów 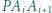 jest równoramienny (przyjmujemy
jest równoramienny (przyjmujemy 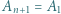 ). Czy stąd wynika, że wielokąt ma okrąg opisany, którego środkiem jest punkt
). Czy stąd wynika, że wielokąt ma okrąg opisany, którego środkiem jest punkt 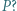
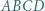 jest wpisany w okrąg. Punkty
jest wpisany w okrąg. Punkty 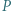 i
i 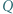 są ortocentrami trójkątów odpowiednio
są ortocentrami trójkątów odpowiednio 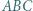 i
i 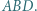 Udowodnić, że
Udowodnić, że 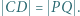
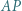 i
i 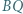 są wysokościami trójkąta nieprostokątnego
są wysokościami trójkąta nieprostokątnego 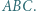 Punkty
Punkty 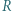 i
i 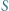 są rzutami prostokątnymi punktów odpowiednio
są rzutami prostokątnymi punktów odpowiednio 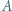 i
i 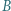 na prostą
na prostą 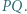 Udowodnić, że
Udowodnić, że 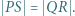
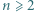 punktów czarnych i
punktów czarnych i 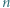 białych. Rysujemy
białych. Rysujemy 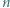 cięciw, z których każda ma jeden koniec biały a drugi czarny. Udowodnić, że można zrobić to tak, by każde dwie narysowane cięciwy przecinały się.
cięciw, z których każda ma jeden koniec biały a drugi czarny. Udowodnić, że można zrobić to tak, by każde dwie narysowane cięciwy przecinały się. cięciw "byle jak" i zastosować rozumowanie podobne do tego, które przedstawiono we wstępie.
cięciw "byle jak" i zastosować rozumowanie podobne do tego, które przedstawiono we wstępie.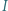 wpisany w trójkąt
wpisany w trójkąt 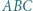 jest styczny do odcinków
jest styczny do odcinków 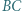 i
i 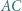 w punktach odpowiednio
w punktach odpowiednio 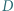 i
i 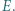 Punkt
Punkt 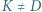 leży na prostej
leży na prostej 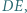 przy czym
przy czym 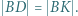 Dowieść, że prosta
Dowieść, że prosta 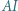 przechodzi przez środek odcinka
przechodzi przez środek odcinka 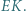
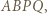 którego przekątna
którego przekątna 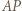 leży na prostej
leży na prostej 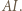 Punkt
Punkt 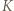 leży na odcinku
leży na odcinku 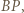 a ponadto
a ponadto 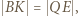 więc czworokąt
więc czworokąt 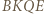 jest równoległobokiem. Z tego wynika, że środek odcinka
jest równoległobokiem. Z tego wynika, że środek odcinka 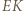 pokrywa się ze środkiem rombu
pokrywa się ze środkiem rombu 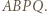
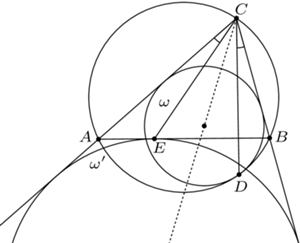
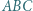 wpisany w okrąg
wpisany w okrąg  Okrąg
Okrąg 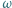 jest styczny do odcinków
jest styczny do odcinków 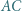 i
i 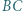 oraz do okręgu
oraz do okręgu  w punkcie
w punkcie 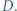 Okrąg
Okrąg 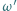 zaś jest dopisany do trójkąta
zaś jest dopisany do trójkąta 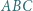 i styczny do boku
i styczny do boku 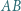 w punkcie
w punkcie 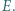 Wykazać, że
Wykazać, że 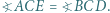
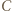 i promieniu
i promieniu 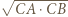 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 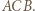 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 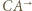 i
i 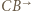 oraz prostą
oraz prostą 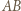 z okręgiem
z okręgiem 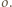 W takim razie okrąg
W takim razie okrąg 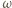 przejdzie na okrąg styczny do prostej
przejdzie na okrąg styczny do prostej 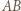 i półprostych
i półprostych 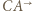 i
i 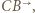 czyli na okrąg
czyli na okrąg 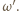 Stąd wniosek, że obrazem punktu
Stąd wniosek, że obrazem punktu 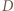 jest punkt
jest punkt 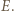 Półprosta
Półprosta 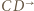 przejdzie więc na półprostą
przejdzie więc na półprostą 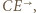 a skoro inwersja zachowuje kąty, to
a skoro inwersja zachowuje kąty, to 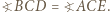
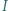 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 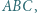 zaś
zaś  jest okręgiem opisanym na tym trójkącie. Okrąg
jest okręgiem opisanym na tym trójkącie. Okrąg 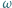 styczny do odcinków
styczny do odcinków 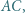
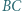 jest styczny do okręgu
jest styczny do okręgu  w punkcie
w punkcie 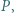 a
a 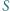 jest środkiem tego łuku
jest środkiem tego łuku 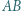 okręgu
okręgu 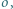 na którym leży punkt
na którym leży punkt 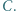 Wykazać, że punkty
Wykazać, że punkty 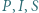 są współliniowe.
są współliniowe.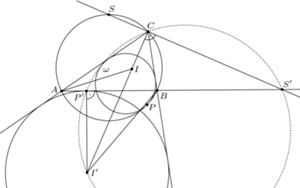
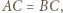 to punkty
to punkty 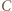 i
i 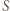 pokrywają się i punkty
pokrywają się i punkty 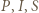 leżą na dwusiecznej
leżą na dwusiecznej 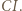 Dalej zakładamy, że
Dalej zakładamy, że 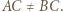 Wówczas punkty
Wówczas punkty 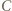 i
i 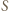 są różne, zaś proste
są różne, zaś proste 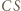 i
i 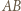 nie są równoległe. Rozważmy złożenie inwersji o środku
nie są równoległe. Rozważmy złożenie inwersji o środku 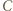 i promieniu
i promieniu 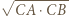 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 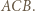 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 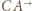 i
i 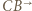 oraz prostą
oraz prostą 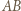 z okręgiem
z okręgiem 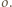 Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu
Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu 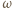 jest okrąg dopisany do trójkąta
jest okrąg dopisany do trójkąta 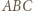 styczny do boku
styczny do boku 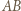 w punkcie
w punkcie 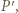 który jest obrazem punktu
który jest obrazem punktu 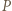 w tym przekształceniu. Ponieważ
w tym przekształceniu. Ponieważ 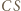 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 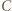 trójkąta
trójkąta 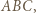 to proste
to proste 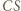 i
i 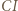 są prostopadłe. W takim razie obrazem punktu
są prostopadłe. W takim razie obrazem punktu 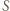 jest punkt
jest punkt 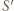 przecięcia prostej
przecięcia prostej 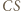 (która jest swoim własnym obrazem) z prostą
(która jest swoim własnym obrazem) z prostą 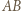 (która jest obrazem okręgu
(która jest obrazem okręgu  ). Niech
). Niech 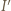 będzie obrazem punktu
będzie obrazem punktu 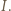 Wtedy z definicji inwersji mamy
Wtedy z definicji inwersji mamy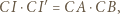
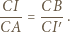
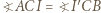 (bo inwersja zachowuje kąty) otrzymujemy, że trójkąty
(bo inwersja zachowuje kąty) otrzymujemy, że trójkąty 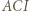 i
i 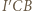 są podobne. W takim razie
są podobne. W takim razie 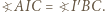 Ponieważ
Ponieważ 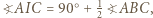 to mamy
to mamy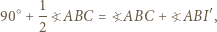
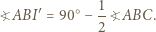
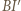 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 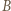 trójkąta
trójkąta 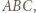 więc
więc 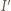 jest środkiem okręgu dopisanego do trójkąta
jest środkiem okręgu dopisanego do trójkąta 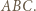 W takim razie
W takim razie 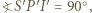 co wraz z równością
co wraz z równością 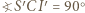 (bo
(bo 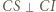 ) oznacza, że punkty
) oznacza, że punkty 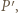
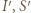 i
i 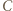 leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty
leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty 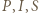 są współliniowe.
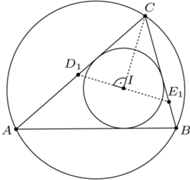
są współliniowe.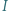 jest wpisany w trójkąt
jest wpisany w trójkąt 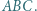 Okrąg
Okrąg 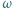 styczny do okręgu opisanego na trójkącie
styczny do okręgu opisanego na trójkącie 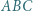 jest styczny do odcinków
jest styczny do odcinków 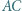 i
i 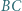 odpowiednio w punktach
odpowiednio w punktach 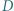 i
i 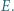 Wykazać, że punkt
Wykazać, że punkt 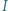 leży na odcinku
leży na odcinku 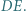
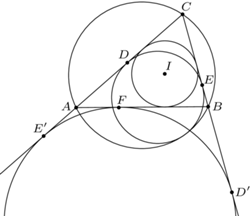
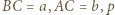 to połowa obwodu trójkąta
to połowa obwodu trójkąta 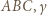 to miara kąta
to miara kąta 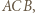 zaś
zaś  to promień okręgu wpisanego w trójkąt
to promień okręgu wpisanego w trójkąt 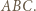 Inwersja o środku
Inwersja o środku 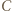 i promieniu
i promieniu 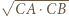 złożona z symetrią względem dwusiecznej kąta
złożona z symetrią względem dwusiecznej kąta 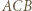 przeprowadza okrąg
przeprowadza okrąg 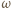 na okrąg dopisany do trójkąta
na okrąg dopisany do trójkąta 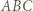 styczny do boku
styczny do boku 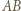 w punkcie
w punkcie 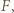 a punkty
a punkty 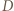 i
i 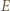 odpowiednio na punkty
odpowiednio na punkty 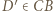 i
i 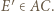 Ponieważ
Ponieważ 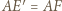 i
i 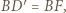 to
to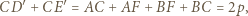
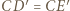 prowadzi do wniosku, że
prowadzi do wniosku, że 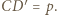 Z drugiej strony z definicji inwersji mamy
Z drugiej strony z definicji inwersji mamy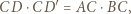
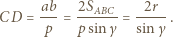
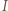 i prostopadła do prostej
i prostopadła do prostej 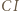 przecina boki
przecina boki 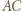 i
i 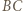 odpowiednio w punktach
odpowiednio w punktach 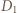 i
i 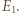 Skoro
Skoro 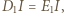 to odległość punktu
to odległość punktu 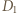 od prostej
od prostej 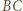 jest równa
jest równa 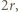 skąd wniosek, że
skąd wniosek, że 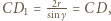 czyli
czyli 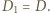 Analogicznie uzasadnimy, że
Analogicznie uzasadnimy, że 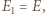 więc punkt
więc punkt 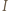 leży na odcinku
leży na odcinku 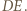
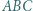 jest wpisany w okrąg
jest wpisany w okrąg 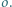 Punkty
Punkty 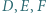 są środkami łuków
są środkami łuków 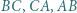 niezawierających pozostałych wierzchołków trójkąta. Punkty
niezawierających pozostałych wierzchołków trójkąta. Punkty 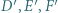 są symetryczne do punktów
są symetryczne do punktów 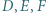 odpowiednio względem boków
odpowiednio względem boków 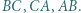 Wykazać, że punkty
Wykazać, że punkty 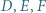 oraz ortocentrum trójkąta
oraz ortocentrum trójkąta 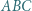 leżą na jednym okręgu.
leżą na jednym okręgu.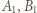 i
i 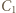 będą spodkami wysokości trójkąta
będą spodkami wysokości trójkąta 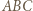 poprowadzonymi odpowiednio z wierzchołków
poprowadzonymi odpowiednio z wierzchołków 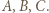 Ponieważ na czworokątach
Ponieważ na czworokątach 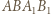 i
i 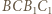 można opisać okręgi, to
można opisać okręgi, to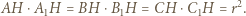
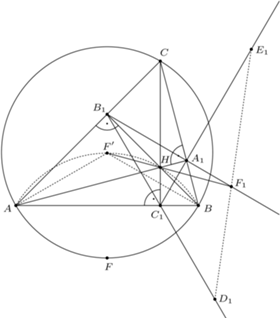
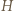 i promieniu
i promieniu  złożoną z symetrią środkową względem punktu
złożoną z symetrią środkową względem punktu 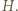 Obrazami punktów
Obrazami punktów 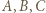 są zatem punkty
są zatem punkty 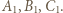 Ponieważ
Ponieważ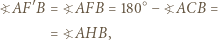
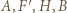 leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą
leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą 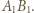 Obrazem punktu
Obrazem punktu 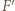 jest punkt
jest punkt 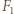 przecięcia prostych
przecięcia prostych 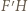 i
i 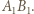 Analogicznie stwierdzamy, że w tym przekształceniu punkt
Analogicznie stwierdzamy, że w tym przekształceniu punkt 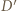 przechodzi na punkt
przechodzi na punkt 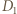 przecięcia prostych
przecięcia prostych 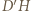 i
i 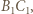 a punkt
a punkt 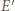 przechodzi na punkt
przechodzi na punkt 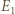 przecięcia prostych
przecięcia prostych 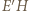 i
i 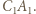
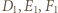 leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta
leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta 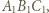 widzimy, że wystarczy wykazać, że
widzimy, że wystarczy wykazać, że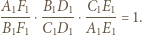
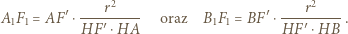
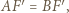 widzimy, że
widzimy, że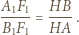

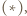 co kończy rozwiązanie.
co kończy rozwiązanie.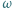 wpisany w trójkąt
wpisany w trójkąt 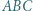 jest styczny do boku
jest styczny do boku 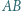 w punkcie
w punkcie 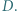 Okrąg
Okrąg 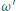 jest styczny do półprostych
jest styczny do półprostych 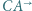 i
i 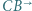 oraz jest styczny zewnętrznie w punkcie
oraz jest styczny zewnętrznie w punkcie 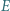 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 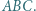 Wykazać, że
Wykazać, że 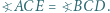
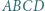 o podstawach
o podstawach 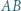 i
i 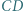 jest wpisany w okrąg
jest wpisany w okrąg 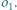 Okrąg
Okrąg 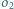 jest styczny do odcinków
jest styczny do odcinków 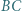 i
i 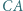 oraz jest styczny wewnętrznie do okręgu
oraz jest styczny wewnętrznie do okręgu 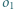 w punkcie
w punkcie 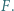 Okrąg wpisany w trójkąt
Okrąg wpisany w trójkąt 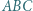 jest styczny do odcinka
jest styczny do odcinka 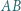 w punkcie
w punkcie 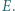 Dowieść, że punkty
Dowieść, że punkty 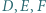 leżą na jednej prostej.
leżą na jednej prostej.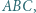 w którym
w którym 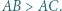 Punkty
Punkty 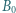 i
i 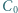 są odpowiednio środkami boków
są odpowiednio środkami boków 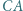 i
i 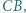 a punkt
a punkt 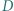 jest spodkiem wysokości opuszczonej z wierzchołka
jest spodkiem wysokości opuszczonej z wierzchołka 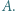 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 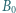 i
i 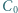 jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 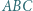 w punkcie
w punkcie 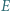 różnym od
różnym od 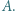 Udowodnić, że środek ciężkości trójkąta
Udowodnić, że środek ciężkości trójkąta 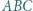 leży na prostej
leży na prostej 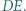
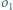 jest styczny do boków
jest styczny do boków 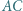 i
i 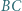 trójkąta
trójkąta 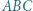 oraz do okręgu opisanego na tym trójkącie w punkcie
oraz do okręgu opisanego na tym trójkącie w punkcie 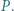 Okrąg
Okrąg 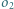 jest styczny do półprostych
jest styczny do półprostych 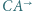 i
i 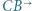 oraz jest styczny zewnętrznie do okręgu opisanego na trójkącie
oraz jest styczny zewnętrznie do okręgu opisanego na trójkącie 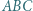 w punkcie
w punkcie 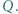 Wykazać, że
Wykazać, że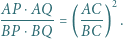
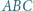 jest wpisany w okrąg
jest wpisany w okrąg 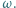 Prosta
Prosta 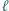 jest równoległa do prostej
jest równoległa do prostej 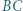 i przecina odcinki
i przecina odcinki 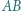 i
i 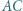 odpowiednio w punktach
odpowiednio w punktach 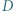 i
i 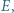 a okrąg
a okrąg 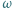 w punktach
w punktach 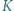 i
i 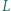 (gdzie
(gdzie 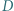 leży między punktami
leży między punktami 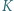 i
i 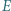 ). Okrąg
). Okrąg 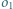 jest styczny do odcinków
jest styczny do odcinków 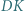 i
i 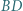 oraz do okręgu
oraz do okręgu  ; okrąg
; okrąg 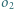 jest styczny do odcinków
jest styczny do odcinków 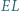 i
i 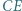 oraz do okręgu
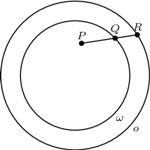
oraz do okręgu  Wyznaczyć miejsce geometryczne punktów przecięcia wspólnych stycznych wewnętrznych okręgów
Wyznaczyć miejsce geometryczne punktów przecięcia wspólnych stycznych wewnętrznych okręgów 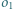 i
i 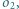 przy zmieniającym się położeniu prostej
przy zmieniającym się położeniu prostej 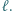
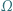 i
i 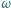 przecinają się w punktach
przecinają się w punktach 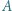 i
i 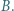 Środek
Środek 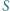 okręgu
okręgu 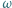 leży na okręgu
leży na okręgu 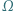 i jest końcem jego średnicy
i jest końcem jego średnicy 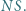 Cięciwa
Cięciwa 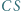 okręgu
okręgu 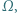 niebędąca średnicą, przecina okrąg
niebędąca średnicą, przecina okrąg 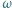 oraz odcinek
oraz odcinek 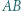 odpowiednio w punktach
odpowiednio w punktach 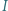 oraz
oraz 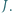 Prosta przechodząca przez
Prosta przechodząca przez 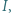 równoległa do
równoległa do 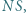 przecina odcinek
przecina odcinek 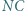 w punkcie
w punkcie 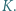 Dowieść, że prosta
Dowieść, że prosta 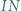 przechodzi przez środek odcinka
przechodzi przez środek odcinka 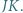

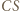 połowi kąt
połowi kąt 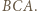 Leżący na nim punkt
Leżący na nim punkt 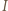 spełnia warunek
spełnia warunek 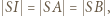 charakteryzujący środek okręgu wpisanego w trójkąt
charakteryzujący środek okręgu wpisanego w trójkąt 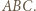 Trójkąt
Trójkąt 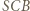 jest podobny do
jest podobny do 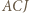 (równe kąty przy wierzchołkach
(równe kąty przy wierzchołkach 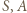 oraz
oraz 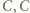 ). Otrzymujemy następujący ciąg proporcji (pierwsza z nich zachodzi, bo
). Otrzymujemy następujący ciąg proporcji (pierwsza z nich zachodzi, bo 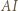 jest dwusieczną kąta
jest dwusieczną kąta 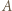 w trójkącie
w trójkącie 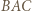 ; druga wynika ze wspomnianego podobieństwa; a ostatnia z równoległości
; druga wynika ze wspomnianego podobieństwa; a ostatnia z równoległości 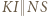 ):
):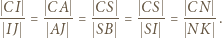
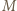 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 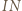 i
i 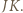 Wystarczy teraz zastosować twierdzenie Menelausa do trójkąta
Wystarczy teraz zastosować twierdzenie Menelausa do trójkąta 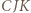 przeciętego prostą
przeciętego prostą 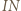 :
: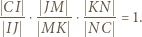
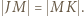
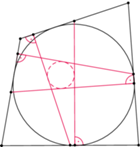
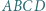 można wpisać okrąg. Przez środek każdego z odcinków
można wpisać okrąg. Przez środek każdego z odcinków 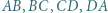 poprowadzono proste prostopadłe do przeciwległych boków czworokąta
poprowadzono proste prostopadłe do przeciwległych boków czworokąta 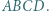 Proste te ograniczają obszar będący czworokątem wypukłym. Wykazać, że w ten czworokąt również można wpisać okrąg.
Proste te ograniczają obszar będący czworokątem wypukłym. Wykazać, że w ten czworokąt również można wpisać okrąg.
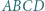 można opisać okrąg. Niech
można opisać okrąg. Niech 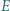 będzie punktem przecięcia przekątnych czworokąta. Załóżmy, że dwusieczna kąta
będzie punktem przecięcia przekątnych czworokąta. Załóżmy, że dwusieczna kąta 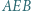 przecina prostą
przecina prostą 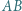 w punkcie
w punkcie 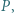 zaś prostą
zaś prostą 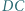 w punkcie
w punkcie 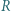 ; niech ponadto dwusieczna kąta
; niech ponadto dwusieczna kąta 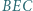 przecina prostą
przecina prostą 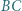 w punkcie
w punkcie 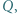 zaś prostą
zaś prostą 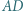 w punkcie
w punkcie 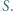 Udowodnić, że okręgi opisane na trójkątach
Udowodnić, że okręgi opisane na trójkątach 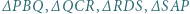 mają punkt wspólny.
mają punkt wspólny.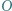 wpisano dwa okręgi:
wpisano dwa okręgi: 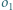 styczny do ramion kąta w punktach
styczny do ramion kąta w punktach 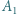 i
i 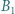 oraz
oraz 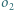 - w punktach
- w punktach 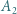 i
i 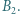 Wykazać, że okręgi te wyznaczają cięciwy jednakowej długości na ich wspólnej siecznej
Wykazać, że okręgi te wyznaczają cięciwy jednakowej długości na ich wspólnej siecznej 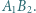
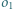 i
i 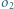 przecinają się w punktach
przecinają się w punktach 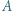 i
i 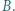 Z punktu
Z punktu 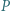 leżącego na prostej
leżącego na prostej 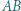 poprowadzono styczną do
poprowadzono styczną do 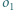 w punkcie
w punkcie 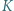 i do
i do 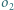 w punkcie
w punkcie 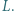 Udowodnić, że trójkąt
Udowodnić, że trójkąt 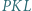 jest równoramienny.
jest równoramienny.