Dowody i obliczenia
Kilka miesięcy temu Marek Kordos zasugerował, że skoro napisałem już w Delcie 12/2014 o tym, czego o równaniu Naviera-Stokesa nie wiadomo, to może napisałbym też artykuł o tym, co z tym równaniem da się zrobić. Tak sformułowana oferta brzmi trochę jak "propozycja nie do odrzucenia", więc nieopatrznie obiecałem taki artykuł dostarczyć. Piszę "nieopatrznie", bo w momencie podjęcia zobowiązania nie uściśliliśmy, co powinienem rozumieć przez stwierdzenie da się zrobić. Czy chodzi o to, co da się udowodnić? Czy raczej o to, co daje się obliczyć?


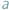 i
i 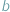 dają tę samą resztę z dzielenia przez liczbę naturalną
dają tę samą resztę z dzielenia przez liczbę naturalną 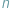 (innymi słowy, jeśli
(innymi słowy, jeśli  jest podzielne przez
jest podzielne przez 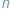 ), uczenie jest stwierdzić, że
), uczenie jest stwierdzić, że 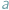 i
i 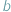 przystają do siebie modulo
przystają do siebie modulo 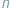 i fakt ten zanotować jako
i fakt ten zanotować jako 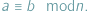 W tym kontekście znaczek "
W tym kontekście znaczek "  " (lub raczej to, co on sobą reprezentuje) nazywamy właśnie kongruencją.
" (lub raczej to, co on sobą reprezentuje) nazywamy właśnie kongruencją.