Szansa na sukces

Metoda probabilistyczna gościła już na łamach Delty (np. w numerach 12/2006 i 4/2015), byłoby jednak nieprawdopodobnie głupio pominąć ją w numerze poświęconym dowodom.

W najbardziej podstawowej wersji może się ona okazać przydatna w sytuacji, gdy chcemy wykazać istnienie obiektu spełniającego określone warunki - wówczas możemy spróbować przedstawić schemat losowania badanych obiektów, w którym z dodatnim prawdopodobieństwem wynik będzie spełniał przedstawione żądania. Opis ten może brzmieć dość enigmatycznie, powinien stać się bardziej zrozumiały po lekturze poniższego rozumowania, uchodzącego za jeden z pierwszych przykładów zastosowania metody probabilistycznej.

Rozważmy graf pełny, którego każde dwa wierzchołki są połączone krawędzią w kolorze niebieskim bądź czerwonym. Okazuje się, co udowodnił Frank Ramsey w 1930 roku, że

Twierdzenie. Dla dowolnie zadanych liczb naturalnych 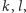$k,l,$ jeśli liczba wierzchołków w grafie pełnym jest dostatecznie duża, istnieje w nim podgraf o 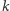$k$ wierzchołkach połączonych wyłącznie niebieskimi krawędziami lub podgraf o 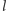$l$ wierzchołkach, z których każde dwa połączone są krawędziami czerwonymi.

Najmniejszy z tych "dostatecznie dużych" rozmiarów wyjściowego grafu nazywamy liczbą Ramseya i oznaczamy przez 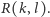$R(k, l).$ W 1947 roku Paul Erdős przedstawił następujące oszacowanie z dołu liczby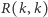 $R(k, k)$

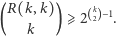(R(k,k) )⩾ 2 k2 −1. k

(*)

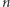Oto jak uzyskał ten wynik: rozważmy graf o $|n$ wierzchołkach, gdzie $n$ jest "niedostatecznie duże", czyli 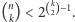$(n) < 2 k2 −1. k$ Pokażemy, że możemy pokolorować krawędzie tego grafu w taki sposób, by nie istniał podgraf rozmiaru 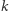$|k$ o wszystkich krawędziach w tym samym kolorze; zatem natychmiastowym wnioskiem będzie nierówność (*).

Każdą z krawędzi naszego grafu pomalujmy na niebiesko z prawdopodobieństwem 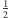$|12$ lub na czerwono z tym samym prawdopodobieństwem. Wybierzmy dowolny podgraf o 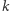$k$ wierzchołkach - wówczas zdarzenie, polegające na pomalowaniu wszystkich krawędzi wybranego podgrafu (których jest 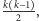$k k−1 --2--,$ inaczej 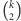$k (2)$ ) na ten sam kolor, ma prawdopodobieństwo 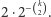$|2⋅2− k2 .$ Podgrafów o 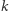$k$ wierzchołkach jest jednak 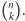$|(n). k$ Szansa na to, że pewien z tych podgrafów ma krawędzie pomalowane na jeden kolor, nie przekracza 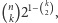$k (nk)21− 2 ,$ zatem zgodnie z założeniem o "niedostatecznie dużym" 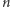$n$ jest mniejsza od 1. W tej sytuacji szansa na to, że żaden z podgrafów o 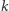$k$ wierzchołkach nie ma wszystkich krawędzi w tym samym kolorze, jest dodatnia, co dowodzi istnienia żądanego kolorowania.