Problem izomorfizmu grafów
Spójrzmy na dwa grafy na poniższym rysunku. Wyglądają zupełnie inaczej, prawda?
Spójrzmy na dwa grafy na poniższym rysunku. Wyglądają zupełnie inaczej, prawda?
Metoda probabilistyczna gościła już na łamach Delty (np. w numerach 12/2006 i 4/2015), byłoby jednak nieprawdopodobnie głupio pominąć ją w numerze poświęconym dowodom.
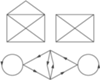
Rys. 1 (a), (b), (c). Linie oznaczone strzałkami można rysować tylko zgodnie z ich kierunkiem
Które z rysunków 1 (a), (b), (c) da się narysować bez odrywania ołówka od kartki i bez rysowania ponownie wzdłuż narysowanej już linii?
Wojtek leżał na podłodze i czytał właśnie książkę o grafach, którą wypożyczył z biblioteki. Alicja, jego młodsza siostra, która przeglądała w tym czasie portal społecznościowy, spytała nagle...
Mimo licznych działań skierowanych na zwalczanie terroryzmu wiele organizacji terrorystycznych wciąż się powiększa. Aby poradzić sobie z tym problemem, agencje bezpieczeństwa poszukują nowych sposobów analizy pozwalających lepiej zrozumieć strukturę tych organizacji. Jednym z problemów jest zidentyfikowanie kluczowych członków organizacji terrorystycznej przy użyciu informacji jedynie o tym, jak wygląda sieć terrorystyczna - dzięki temu agencje bezpieczeństwa mogłyby skupić swoje ograniczone zasoby na tych jednostkach. W tym artykule omówimy nowe podejście do tego problemu oparte na teorii gier.
Zadanie 44 w książce 100 zadań Hugona Steinhausa dotyczy zamkniętych dróg po krawędziach wielościanu foremnego, które przechodzą dokładnie jeden raz przez każdy wierzchołek, czyli złożonych z krawędzi cykli Hamiltona. Chodzi o to, aby znaleźć wszystkie kształty takich cykli i policzyć, ile ich jest (z dokładnością do położenia) dla każdego wielościanu foremnego.
Teoria grafów to gałąź matematyki, do której powstania impuls dało liczące sobie już ćwierć tysiąclecia słynne zagadnienie mostów królewieckich, rozwiązane przez Leonharda Eulera. Osobiście lubię patrzeć na matematykę nie tylko jako na zbiór problemów ciekawych samych w sobie, ale również jak na model rzeczywistości, narzędzie pozwalające efektywniej radzić sobie z rzeczywistymi zmartwieniami. Obecnie teoria grafów staje się jednym z najpopularniejszych takich narzędzi, używanym chętnie przez matematyków (na rzecz innych gałęzi tej nauki), informatyków, fizyków, chemików, a nawet socjologów. Niniejszy artykuł ma na celu przedstawienie tego, jak zagadnienie kolorowania grafów służyć może za narzędzie przydatne w przydzielaniu częstotliwości nadajnikom w jednym z modeli sieci radiowej.
Zajmijmy się następującym klasycznym zadaniem: należy pokryć kwadrat jednostkowy kwadratowymi kafelkami o różnych bokach tak, aby żadne dwa kafelki nie nachodziły na siebie. Czytelnik może spróbować poszukać takiego kafelkowania metodą prób i błędów, ale na pierwszy rzut oka nie jest jasne, czy pokrycie o żądanych własnościach w ogóle istnieje...
Przedstawimy tu dwa zagadnienia, w których pojawia się problem znajdowania najliczniejszego skojarzenia w grafie dwudzielnym, jednak trochę ukryty.
Cztery parametry. Tym, co najczęściej robi się w grafach dwudzielnych, jest znajdowanie najliczniejszego skojarzenia. Można jednak rozważać aż cztery – parami dualne – parametry powiązane z najliczniejszym skojarzeniem...
Kiedy wędrujemy po pustyni i poczujemy zmęczenie, poszukujemy najbliższej oazy, w której moglibyśmy zregenerować siły. Jeśli mamy szczęście, możemy spotkać na pustyni beduina, który wskaże nam właściwy kierunek do oazy. Czy rzeczywiście właściwy?
Pierwszy "dowód" twierdzenia o czterech barwach pojawił się w roku 1879. Przedstawił go Alfred Kempe, londyński prawnik. Był to zapewne najsłynniejszy "fałszywy dowód" w całej historii matematyki...
Historia twierdzenia o czterech barwach sięga roku 1852, kiedy to student Francis Guthrie, wiedziony czysto praktycznymi pobudkami, postawił swemu wykładowcy, Augustowi De Morganowi, następujące pytanie: jaka jest najmniejsza liczba kolorów, która wystarcza do pokolorowania dowolnej płaskiej mapy w taki sposób, aby każde dwa państwa, które graniczą ze sobą, otrzymały różne kolory?
Skojarzenia to bardzo popularny temat. Pojawiają się w różnych miejscach zarówno w informatyce, jak i w matematyce dyskretnej.
Ludzie od niepamiętnych czasów prześcigali się w biciu rekordów w najprzeróżniejszych dziedzinach, od czysto sportowych (szybciej, wyżej, mocniej), poprzez cywilizacyjne (wyższe budowle, większe samoloty, szybsze komputery), aż po całkiem absurdalne, żeby nie powiedzieć głupie.