Zadanie ZM-1479
o zadaniu...
- Publikacja w Delcie: grudzień 2015
- Publikacja elektroniczna: 30-11-2015
Wykazać, że w grafie prostym (tj. skończonym zbiorze wierzchołków, spośród których pewne są połączone nieskierowanymi pojedynczymi krawędziami, bez pętli) o co najmniej dwóch wierzchołkach istnieją dwa wierzchołki o tym samym stopniu.
Uwaga. Stopień wierzchołka to liczba krawędzi w nim zaczepionych.
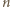wierzchołków, 
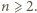Zauważmy, że stopień każdego wierzchołka może wynosić 
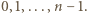Gdyby stopnie wszystkich wierzchołków były różne, to w szczególności istniałby wierzchołek o stopniu 
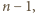połączony krawędzią z każdym z pozostałych wierzchołków. Wtedy jednak nie mógłby istnieć wierzchołek o stopniu 0.