W rozwiązaniu tego zadania odwołamy się do teorii grafów. Skorzystamy z powszechnie znanego i nietrudnego w dowodzie faktu: w dowolnym grafie prostym o 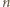 wierzchołkach i
wierzchołkach i 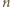 krawędziach istnieje cykl. Przypomnijmy, że w grafie prostym nie ma podwójnych krawędzi ani pętli.
krawędziach istnieje cykl. Przypomnijmy, że w grafie prostym nie ma podwójnych krawędzi ani pętli.
Dla dowodu nie wprost załóżmy, że usunięcie dowolnej z kolumn spowoduje powstanie tablicy o dwóch identycznych wierszach. Oznacza to, że dla każdej z kolumn istnieje para wierszy, która różni się między sobą tylko w tej kolumnie. Rozważmy więc graf, którego wierzchołkami są wiersze naszej tablicy i połączmy dwa wiersze krawędzią, jeżeli dla pewnej kolumny są one tymi wierszami, które różnią się tylko w niej. Jeśli dla pewnej kolumny istnieje więcej takich par wierszy, to wybierzmy z nich dowolną i tylko między nimi poprowadźmy krawędź w naszym grafie. Oczywiście, jedna para wierszy zostanie połączona krawędzią co najwyżej raz - nie może bowiem zdarzyć się sytuacja, w której dwa wiersze różnią się na tylko jednej pozycji dla dwóch różnych pozycji. Utworzona przez nas struktura jest więc  -wierzchołkowym grafem prostym o
-wierzchołkowym grafem prostym o  krawędziach. Z przytoczonego wcześniej faktu wynika istnienie cyklu w tym grafie. Innymi słowy, istnieje ciąg wierszy o numerach
krawędziach. Z przytoczonego wcześniej faktu wynika istnienie cyklu w tym grafie. Innymi słowy, istnieje ciąg wierszy o numerach 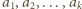 o tej własności, że dla dowolnego
o tej własności, że dla dowolnego 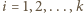 wiersze
wiersze 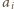 oraz
oraz 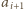 różnią się na dokładnie jednej pozycji (przyjmujemy, że
różnią się na dokładnie jednej pozycji (przyjmujemy, że 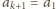 ). Oznaczmy przez
). Oznaczmy przez 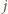 numer pozycji, na której różnią się wiersze o numerach
numer pozycji, na której różnią się wiersze o numerach 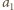 i
i 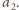 Każda kolejna para wierszy różni się już w innej kolumnie niż
Każda kolejna para wierszy różni się już w innej kolumnie niż 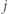 -ta. Począwszy więc od wiersza o numerze
-ta. Począwszy więc od wiersza o numerze 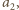 każdy następny wiersz w naszym ciągu zawiera tą samą liczbę
każdy następny wiersz w naszym ciągu zawiera tą samą liczbę 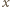 na pozycji
na pozycji 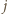 -tej. Ale wiersze
-tej. Ale wiersze 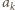 oraz
oraz 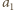 różnią się również w innej kolumnie niż
różnią się również w innej kolumnie niż 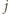 -ta, a zatem wiersz
-ta, a zatem wiersz 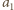 zawiera liczbę
zawiera liczbę  na pozycji
na pozycji 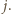 Otrzymana sprzeczność kończy rozwiązanie zadania.
Otrzymana sprzeczność kończy rozwiązanie zadania.
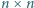 wpisano liczbę rzeczywistą w taki sposób, że każde dwa wiersze są różne (czyli różnią się na co najmniej jednej pozycji). Udowodnić, że z danej tablicy można usunąć pewną kolumnę tak, aby ta własność została zachowana.
wpisano liczbę rzeczywistą w taki sposób, że każde dwa wiersze są różne (czyli różnią się na co najmniej jednej pozycji). Udowodnić, że z danej tablicy można usunąć pewną kolumnę tak, aby ta własność została zachowana.
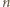 wierzchołkach i
wierzchołkach i 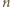 krawędziach istnieje cykl. Przypomnijmy, że w grafie prostym nie ma podwójnych krawędzi ani pętli.
krawędziach istnieje cykl. Przypomnijmy, że w grafie prostym nie ma podwójnych krawędzi ani pętli. -wierzchołkowym grafem prostym o
-wierzchołkowym grafem prostym o  krawędziach. Z przytoczonego wcześniej faktu wynika istnienie cyklu w tym grafie. Innymi słowy, istnieje ciąg wierszy o numerach
krawędziach. Z przytoczonego wcześniej faktu wynika istnienie cyklu w tym grafie. Innymi słowy, istnieje ciąg wierszy o numerach 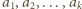 o tej własności, że dla dowolnego
o tej własności, że dla dowolnego 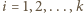 wiersze
wiersze 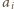 oraz
oraz 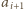 różnią się na dokładnie jednej pozycji (przyjmujemy, że
różnią się na dokładnie jednej pozycji (przyjmujemy, że 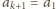 ). Oznaczmy przez
). Oznaczmy przez 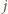 numer pozycji, na której różnią się wiersze o numerach
numer pozycji, na której różnią się wiersze o numerach 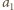 i
i 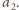 Każda kolejna para wierszy różni się już w innej kolumnie niż
Każda kolejna para wierszy różni się już w innej kolumnie niż 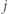 -ta. Począwszy więc od wiersza o numerze
-ta. Począwszy więc od wiersza o numerze 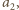 każdy następny wiersz w naszym ciągu zawiera tą samą liczbę
każdy następny wiersz w naszym ciągu zawiera tą samą liczbę 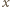 na pozycji
na pozycji 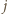 -tej. Ale wiersze
-tej. Ale wiersze 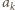 oraz
oraz 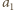 różnią się również w innej kolumnie niż
różnią się również w innej kolumnie niż 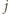 -ta, a zatem wiersz
-ta, a zatem wiersz 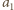 zawiera liczbę
zawiera liczbę  na pozycji
na pozycji 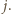 Otrzymana sprzeczność kończy rozwiązanie zadania.
Otrzymana sprzeczność kończy rozwiązanie zadania.