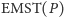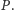Diagramy Woronoja, czyli co widać z góry?
Kiedy wędrujemy po pustyni i poczujemy zmęczenie, poszukujemy najbliższej oazy, w której moglibyśmy zregenerować siły. Jeśli mamy szczęście, możemy spotkać na pustyni beduina, który wskaże nam właściwy kierunek do oazy. Czy rzeczywiście właściwy?
Gdybyśmy mogli unieść się w górę, zobaczylibyśmy interesujące nas obiekty znajdujące się w okolicy. Jak szybko określić, który z nich jest najbliżej? W tym celu moglibyśmy wykorzystać diagram Woronoja.
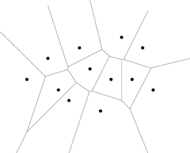
Rys. 1 Diagram Woronoja
Załóżmy, że obiektom, którymi jesteśmy zainteresowani,
odpowiada zbiór
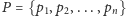 punktów na
płaszczyźnie, które będziemy nazywać centrami. Odległość między
punktami
punktów na
płaszczyźnie, które będziemy nazywać centrami. Odległość między
punktami
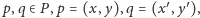 definiujemy jako
definiujemy jako
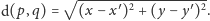
Definicja 1. Dla każdego centrum
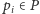 obszar Woronoja
obszar Woronoja
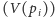 składa się z tych punktów
płaszczyzny, dla których żadne inne centrum nie znajduje się bliżej niż
składa się z tych punktów
płaszczyzny, dla których żadne inne centrum nie znajduje się bliżej niż
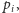 tzn.
tzn.
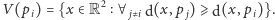 Punkty
należące do brzegów obszarów Woronoja tworzą diagram Woronoja.
Punkty
należące do brzegów obszarów Woronoja tworzą diagram Woronoja.
Zauważmy, że centrum zawsze należy do odpowiadającego mu obszaru.
Co więcej, do każdego obszaru należy tylko jedno centrum. Granicę między
obszarami dla dwóch centrów
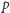 i
i
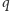 wyznacza symetralna
odcinka
wyznacza symetralna
odcinka
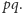 Zatem obszar Woronoja dla
Zatem obszar Woronoja dla
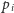 jest częścią wspólną
półpłaszczyzn wyznaczanych przez symetralne odcinków
jest częścią wspólną
półpłaszczyzn wyznaczanych przez symetralne odcinków
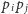 (dla
(dla
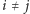 ) i zawierających
) i zawierających
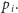 Stąd wniosek, że obszary Woronoja są
wielokątami wypukłymi (ograniczonymi lub nie), a krawędzie diagramu
Woronoja są odcinkami lub półprostymi. Liczba krawędzi diagramu
Woronoja jest liniowa względem liczby centrów, co uzasadnimy nieco
dalej.
Stąd wniosek, że obszary Woronoja są
wielokątami wypukłymi (ograniczonymi lub nie), a krawędzie diagramu
Woronoja są odcinkami lub półprostymi. Liczba krawędzi diagramu
Woronoja jest liniowa względem liczby centrów, co uzasadnimy nieco
dalej.
Wierzchołki diagramu Woronoja znajdują się w tej samej odległości od co najmniej trzech najbliższych centrów. Aby uprościć dalsze rozważania, przyjmijmy, że wierzchołek diagramu jest częścią wspólną dokładnie trzech obszarów Woronoja. Wtedy centra obszarów mających wspólny wierzchołek wyznaczają trójkąt. Ponieważ przeciwległe wierzchołki czworokąta nie mogą wyznaczać dwóch par sąsiadujących obszarów Woronoja, więc dwie różne krawędzie takich trójkątów nie mają innych punktów wspólnych niż końce. Wszystkie zdefiniowane w ten sposób trójkąty tworzą tzw. triangulację Delaunay.
Definicja 2. Triangulacja Delaunay to graf dualny do diagramu Woronoja. Wierzchołki triangulacji (centra obszarów) odpowiadają ścianom diagramu Woronoja (obszarom Woronoja). Natomiast odpowiednikami krawędzi triangulacji są krawędzie diagramu.
Zauważmy, że odpowiadające sobie krawędzie nie muszą się przecinać.
Triangulacja Delaunay jest grafem planarnym, a krawędzie ściany zewnętrznej
wyznaczają otoczkę wypukłą zbioru
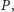 tzn. brzeg najmniejszego zbioru
wypukłego zawierającego
tzn. brzeg najmniejszego zbioru
wypukłego zawierającego
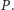 Innymi słowy, wierzchołkami tej
otoczki wypukłej są centra nieograniczonych obszarów Woronoja zbioru
Innymi słowy, wierzchołkami tej
otoczki wypukłej są centra nieograniczonych obszarów Woronoja zbioru
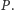 Z własności grafów planarnych (twierdzenie Eulera) otrzymujemy,
że liczba krawędzi triangulacji Delaunay jest liniowa względem liczby centrów.
To pokazuje zarazem, że liczba krawędzi diagramu Woronoja jest liniowa
względem liczby centrów.
Z własności grafów planarnych (twierdzenie Eulera) otrzymujemy,
że liczba krawędzi triangulacji Delaunay jest liniowa względem liczby centrów.
To pokazuje zarazem, że liczba krawędzi diagramu Woronoja jest liniowa
względem liczby centrów.
Wierzchołki trójkąta należącego do triangulacji Delaunay wyznaczają
okrąg o środku w wierzchołku diagramu Woronoja (gdyby na okręgu
znajdowało się więcej centrów z
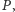 to wyznaczany przez nie wielokąt
moglibyśmy striangulować na różne sposoby). Spróbujmy uogólnić ten
fakt.
to wyznaczany przez nie wielokąt
moglibyśmy striangulować na różne sposoby). Spróbujmy uogólnić ten
fakt.
Twierdzenie 1. Odcinek
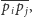 gdzie
gdzie
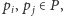 należy do
triangulacji Delaunay wtedy i tylko wtedy, gdy istnieje okrąg przechodzący
przez
należy do
triangulacji Delaunay wtedy i tylko wtedy, gdy istnieje okrąg przechodzący
przez
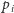 i
i
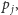 który nie zawiera w swoim wnętrzu punktów
z
który nie zawiera w swoim wnętrzu punktów
z
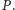
Dowód. Implikacja w prawą stronę wynika z konstrukcji triangulacji
Delaunay. Musimy wykazać implikację w przeciwnym kierunku. Środek
okręgu przechodzącego przez
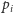 i
i
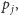 który nie zawiera
w swoim wnętrzu punktów z
który nie zawiera
w swoim wnętrzu punktów z
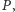 z definicji należy do krawędzi
diagramu Woronoja oddzielającej
z definicji należy do krawędzi
diagramu Woronoja oddzielającej
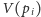 i
i
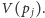 Zatem
odcinek
Zatem
odcinek
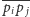 jest krawędzią triangulacji Delaunay.
jest krawędzią triangulacji Delaunay.

Rys. 2 Triangulacja Delaunay i euklidesowe minimalne drzewo rozpinające
Pokażmy jeszcze jedną ciekawą własność triangulacji Delaunay.
Definicja 3. Euklidesowe
minimalne drzewo rozpinające dla zbioru punktów
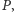 które
oznaczamy przez
które
oznaczamy przez
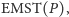 jest drzewem łączącym wszystkie punkty
z
jest drzewem łączącym wszystkie punkty
z
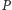 i minimalizującym całkowitą długość krawędzi.
i minimalizującym całkowitą długość krawędzi.
Dowód. Załóżmy, że teza nie jest prawdziwa.
Niech
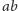 będzie krawędzią
będzie krawędzią
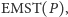 która nie należy
do triangulacji Delaunay zbioru
która nie należy
do triangulacji Delaunay zbioru
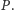 Wtedy, zgodnie z poprzednim
twierdzeniem, okrąg o średnicy
Wtedy, zgodnie z poprzednim
twierdzeniem, okrąg o średnicy
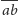 zawiera w swoim
wnętrzu punkt
zawiera w swoim
wnętrzu punkt
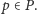 Odcinki
Odcinki
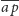 i
i
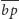 są krótsze od
są krótsze od
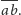 Zatem krawędź
Zatem krawędź
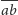 możemy zastąpić jednym z nich,
nie niszcząc spójności grafu i zmniejszając całkowitą długość jego
krawędzi. Jest to sprzeczne z założeniem, że
możemy zastąpić jednym z nich,
nie niszcząc spójności grafu i zmniejszając całkowitą długość jego
krawędzi. Jest to sprzeczne z założeniem, że
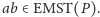
W obliczeniach numerycznych ma zastosowanie jeszcze jedna, znacznie
trudniejsza do udowodnienia, własność triangulacji Delaunay. Uporządkujmy
niemalejąco kąty wszystkich trójkątów tworzących dowolną triangulację
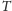 zbioru
zbioru
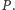 Następnie uporządkujmy leksykograficznie
wszystkie triangulacje zbioru
Następnie uporządkujmy leksykograficznie
wszystkie triangulacje zbioru
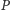 tzn. dla
tzn. dla
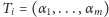 oraz
oraz
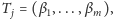 zachodzi
zachodzi

oraz

Wtedy triangulacja Delaunay będzie ostatnim elementem tego porządku, tzn. triangulacja ta maksymalizuje minimalny kąt w tworzących ją trójkątach.
Wiedząc, że diagram Woronoja i triangulacja Delaunay mają tyle interesujących własności, spróbujmy skonstruować te grafy. Oczywiście, na mocy ich dualności wystarczy znaleźć tylko jeden z nich. Aby wyznaczyć diagram Woronoja, można zastosować pewne standardowe metody, np. „dziel i zwyciężaj” lub zamiatanie.
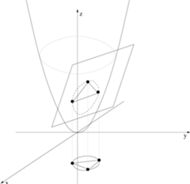
Rys. 3 Rzut trójkąta triangulacji Delaunay na paraboloidę
Ale my znów spróbujemy unieść się w górę. Mianowicie, załóżmy, że
punkty ze zbioru
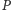 należą do płaszczyzny
należą do płaszczyzny
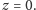 Zrzutujmy
zbiór
Zrzutujmy
zbiór
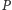 równolegle do osi
równolegle do osi
 na paraboloidę obrotową
na paraboloidę obrotową
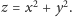 Zauważmy, że obrazy punktów należących do okręgu
zawartego w płaszczyźnie
Zauważmy, że obrazy punktów należących do okręgu
zawartego w płaszczyźnie
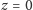 będą współpłaszczyznowe. Rzeczywiście,
jeśli punkt
będą współpłaszczyznowe. Rzeczywiście,
jeśli punkt
 spełnia równanie
spełnia równanie
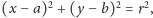 to
w przestrzeni trójwymiarowej punkt
to
w przestrzeni trójwymiarowej punkt
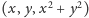 należy do
płaszczyzny
należy do
płaszczyzny
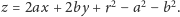 Zatem rzuty okręgów opisanych
na trójkątach triangulacji Delaunay wyznaczają płaszczyzny przecinające
paraboloidę i zawierające rzuty wierzchołków odpowiednich trójkątów. Co
więcej, na mocy wypukłości paraboloidy obrotowej płaszczyzny te nie
rozdzielają obrazów punktów z
Zatem rzuty okręgów opisanych
na trójkątach triangulacji Delaunay wyznaczają płaszczyzny przecinające
paraboloidę i zawierające rzuty wierzchołków odpowiednich trójkątów. Co
więcej, na mocy wypukłości paraboloidy obrotowej płaszczyzny te nie
rozdzielają obrazów punktów z
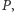 gdyż wnętrza okręgów opisanych
na trójkątach triangulacji Delaunay (których rzuty są odcinane z paraboloidy
przez omawiane płaszczyzny) nie zawierają punktów z
gdyż wnętrza okręgów opisanych
na trójkątach triangulacji Delaunay (których rzuty są odcinane z paraboloidy
przez omawiane płaszczyzny) nie zawierają punktów z
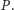 Zatem rzuty
ścian triangulacji Delaunay są ścianami otoczki wypukłej obrazów
punktów z
Zatem rzuty
ścian triangulacji Delaunay są ścianami otoczki wypukłej obrazów
punktów z
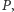 a rzuty krawędzi triangulacji są krawędziami otoczki
wypukłej.
a rzuty krawędzi triangulacji są krawędziami otoczki
wypukłej.
Zatem nie pozostaje nam nic innego, jak znaleźć otoczkę wypukłą zbioru
punktów w przestrzeni trójwymiarowej. Możemy to zrobić, stosując np.
metodę „dziel i zwyciężaj”. Złożoność obliczeniowa tego algorytmu wynosi
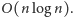 Następnie rzutujemy z powrotem na płaszczyznę
Następnie rzutujemy z powrotem na płaszczyznę
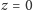 ściany otoczki wypukłej ograniczające ją od dołu i w ten sposób
otrzymujemy triangulację Delaunay zbioru
ściany otoczki wypukłej ograniczające ją od dołu i w ten sposób
otrzymujemy triangulację Delaunay zbioru
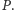 Ponieważ wszystkie
rzutowania możemy wykonać w czasie
Ponieważ wszystkie
rzutowania możemy wykonać w czasie
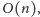 więc całkowita
złożoność tego algorytmu wynosi
więc całkowita
złożoność tego algorytmu wynosi
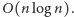 Jest on więc nie tylko
prosty, ale też efektywny.
Jest on więc nie tylko
prosty, ale też efektywny.
Algorytm
Dane: Zbiór
 punktów
punktów
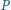 na płaszczyźnie
na płaszczyźnie
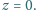
Wynik: Triangulacja Delaunay zbioru
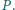
Zrzutuj zbiór
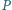 równolegle do osi
równolegle do osi
 na paraboloidę
na paraboloidę
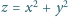 ;
;
Znajdź otoczkę wypukłą zbioru obrazów punktów z
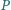 ; Zrzutuj
prostopadle ściany otoczki wypukłej ograniczające ją od dołu na płaszczyznę
; Zrzutuj
prostopadle ściany otoczki wypukłej ograniczające ją od dołu na płaszczyznę
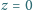 ;
;
return Graf powstały na płaszczyźnie
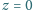 ;
;
Można również wykazać, że rzut prostopadły na płaszczyznę
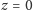 minimalnego wielościanu wypukłego
minimalnego wielościanu wypukłego
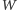 zawierającego
paraboloidę
zawierającego
paraboloidę
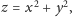 którego ściany zawierają się w płaszczyznach
stycznych do tej paraboloidy w obrazach punktów z
którego ściany zawierają się w płaszczyznach
stycznych do tej paraboloidy w obrazach punktów z
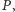 jest diagramem
Woronoja zbioru
jest diagramem
Woronoja zbioru
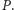 Dowód tego faktu pozostawiamy Czytelnikowi jako
ćwiczenie.
Dowód tego faktu pozostawiamy Czytelnikowi jako
ćwiczenie.