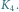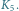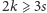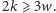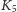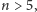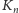Deltoid
Domki i studnie
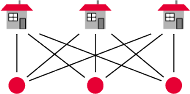
Rys. 1
Zagadka. Bracia Jacek, Wacek i Placek
mieszkają w trzech różnych domkach, w pobliżu których znajdują się
trzy studnie: jedna z
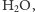 druga z
druga z
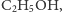 trzecia z sokiem
porzeczkowym. Każdy z braci chciałby poprowadzić ze swojego domu trzy
chodniki, po jednym do każdej ze studni. Czy bracia mogą poprowadzić
swoich 9 chodników tak, aby żadne dwa z nich się nie przecinały (Rys. 1)?
trzecia z sokiem
porzeczkowym. Każdy z braci chciałby poprowadzić ze swojego domu trzy
chodniki, po jednym do każdej ze studni. Czy bracia mogą poprowadzić
swoich 9 chodników tak, aby żadne dwa z nich się nie przecinały (Rys. 1)?
Zapewne wielu Czytelników jeszcze w dzieciństwie przekonało się, metodą prób i błędów, że odpowiedź brzmi „nie”. Aby ją udowodnić, wprowadźmy kilka pojęć z teorii grafów.
Grafy dwudzielne.

Rys. 2 Sytuacje niedozwolone w grafach prostych.
Graf to, mówiąc intuicyjnie, punkty (zwane wierzchołkami) połączone liniami (niekoniecznie prostymi, zwanymi krawędziami). Rozważać będziemy tylko grafy spójne, czyli „w jednym kawałku”, i proste, czyli takie, w których każda krawędź ma dwa różne końce i żadnych dwóch wierzchołków nie łączy bezpośrednio więcej niż jedna krawędź (Rys. 2).
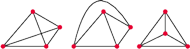
Rys. 3 Różne sposoby narysowania grafu
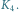
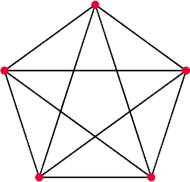
Rys. 4 Grafu
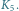
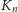 oznacza graf pełny o
oznacza graf pełny o
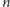 wierzchołkach, czyli graf o
wierzchołkach, czyli graf o
 wierzchołkach, z których każde dwa są połączone krawędzią
(Rys. 3 i Rys. 4).
wierzchołkach, z których każde dwa są połączone krawędzią
(Rys. 3 i Rys. 4).
Graf pełny dwudzielny
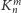 to taki graf, którego
to taki graf, którego
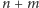 wierzchołków
można podzielić na dwie grupy, po
wierzchołków
można podzielić na dwie grupy, po
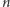 i
i
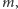 a krawędzie łączą
wszystkie wierzchołki z jednej grupy ze wszystkimi z drugiej, przy czym innych
krawędzi nie ma. W przypadku trzech domków i trzech studni występuje graf
a krawędzie łączą
wszystkie wierzchołki z jednej grupy ze wszystkimi z drugiej, przy czym innych
krawędzi nie ma. W przypadku trzech domków i trzech studni występuje graf
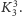
Grafy planarne.
Graf nazywamy planarnym, jeśli da się go narysować na płaszczyźnie tak, aby
żadne dwie krawędzie się nie przecinały. Na przykład graf
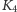 jest
planarny (Rys. 3). Nie wszystkie grafy są planarne.
jest
planarny (Rys. 3). Nie wszystkie grafy są planarne.
W zagadce o domkach i studniach należy rozstrzygnąć, czy graf
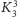 jest
planarny.
jest
planarny.
Wzór Eulera i przydatna nierówność.
Dla grafów planarnych zachodzi wzór Eulera:

gdzie
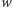 to liczba wierzchołków grafu,
to liczba wierzchołków grafu,
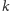 – liczba krawędzi, a
– liczba krawędzi, a
 – liczba ścian, czyli obszarów, na jakie graf dzieli płaszczyznę
(wliczamy też „zewnętrze” grafu).
– liczba ścian, czyli obszarów, na jakie graf dzieli płaszczyznę
(wliczamy też „zewnętrze” grafu).
Wykażemy teraz, że w planarnym grafie dwudzielnym zachodzi nierówność
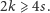 | (*) |
Policzmy krawędzie takiego grafu. Każda ściana ma na przemian wierzchołki
z każdej z dwóch grup, zatem jest parzystokątna, więc co najmniej
czworokątna. Ma wobec tego co najmniej 4 krawędzie. W grafie jest więc
co najmniej
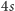 krawędzi, ale – uwaga! – policzonych dwukrotnie
(każdą krawędź liczymy przy każdej z dwóch ścian, które rozdziela). Stąd
krawędzi, ale – uwaga! – policzonych dwukrotnie
(każdą krawędź liczymy przy każdej z dwóch ścian, które rozdziela). Stąd
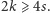
Rozwiązanie zagadki.
Pokażemy, że graf
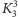 nie jest planarny, czyli że bracia nie są
w stanie poprowadzić nieprzecinających się chodników. Przypuśćmy
przeciwnie. Wtedy ze wzoru Eulera mamy
nie jest planarny, czyli że bracia nie są
w stanie poprowadzić nieprzecinających się chodników. Przypuśćmy
przeciwnie. Wtedy ze wzoru Eulera mamy
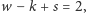 przy czym
przy czym
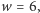
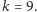 Stąd
Stąd
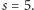 Jednocześnie na mocy (*)
zachodzi
Jednocześnie na mocy (*)
zachodzi
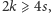 czyli
czyli
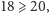 sprzeczność.
sprzeczność.
Zadania domowe
Zadanie 2. Wykaż, że wierzchołki i krawędzie dowolnego wielościanu wypukłego tworzą graf planarny prosty.
Ważna uwaga na koniec. Z rozwiązania zagadki o domkach i studniach oraz
z zadania 4 można wywnioskować, że jeśli graf zawiera „fragment typu”
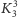 lub
lub
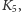 to nie może być planarny (ponieważ już ten
fragment nie daje się narysować bez przecinających się krawędzi, a co dopiero
cały graf).
to nie może być planarny (ponieważ już ten
fragment nie daje się narysować bez przecinających się krawędzi, a co dopiero
cały graf).
Twierdzenie Kuratowskiego głosi, że zachodzi także fakt odwrotny, czyli że
graf jest nieplanarny wtedy i tylko wtedy, gdy zawiera „fragment typu”
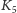 lub
lub
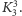 Twierdzenie to oznacza, że te dwa niezwykle proste
grafy nieplanarne (
Twierdzenie to oznacza, że te dwa niezwykle proste
grafy nieplanarne (
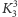 i
i
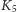 ) wystarczają, by rozstrzygać
o planarności lub nieplanarności wszystkich innych grafów, a także że –
w pewnym sensie – nie ma żadnego „naprawdę zupełnie innego” od nich
grafu nieplanarnego.
) wystarczają, by rozstrzygać
o planarności lub nieplanarności wszystkich innych grafów, a także że –
w pewnym sensie – nie ma żadnego „naprawdę zupełnie innego” od nich
grafu nieplanarnego.