Co to jest?
Miara
Człowiek to istota nie tylko myśląca, ale i mierząca - można by rzec górnolotnie, że mierzenie (rozmiarów wrogiej armii, zaopatrzenia spichrzów, stanu skarbca itp.) leży u podstaw naszej cywilizacji. W języku matematyki miara jest definiowana przez następujące, zdroworozsądkowe warunki...
Po pierwsze, jest to funkcja, która podzbiorom pewnej przestrzeni przyporządkowuje liczby nieujemne (np. miarą pewnego podzbioru przestrzeni powietrznej ograniczonej balonikiem jest 100 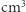 ). Po drugie, jakąkolwiek przestrzeń rozpatrujemy, jej pusty podzbiór ma miarę 0 (tak jak pusty skarbiec czy nienapompowany balonik). Po trzecie, jeśli połączę wiele rozłącznych podzbiorów w jeden, to miara tak powstałego podzbioru ma być sumą miar podzbiorów wyjściowych (tutaj "wiele" może również oznaczać "przeliczalnie wiele", szczegóły można znaleźć w artykułach Michała Korcha i Marty Szumańskiej w Delcie 4/2019).
). Po drugie, jakąkolwiek przestrzeń rozpatrujemy, jej pusty podzbiór ma miarę 0 (tak jak pusty skarbiec czy nienapompowany balonik). Po trzecie, jeśli połączę wiele rozłącznych podzbiorów w jeden, to miara tak powstałego podzbioru ma być sumą miar podzbiorów wyjściowych (tutaj "wiele" może również oznaczać "przeliczalnie wiele", szczegóły można znaleźć w artykułach Michała Korcha i Marty Szumańskiej w Delcie 4/2019).
Czy każdy podzbiór dowolnej przestrzeni możemy zmierzyć? Okazuje się, że mogą być z tym problemy. Dla przykładu, nie istnieje miara 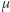 określona na wszystkich podzbiorach zbioru liczb rzeczywistych w taki sposób, że miara dowolnego odcinka jest dodatnia i skończona oraz przesuwając zbiór na prostej, nie zmieniamy jego miary (uzasadnienie na marginesie). Ważne jest zatem, aby definiując miarę, zaznaczyć, jaka jest jej dziedzina, czyli jakie zbiory są względem niej mierzalne.
określona na wszystkich podzbiorach zbioru liczb rzeczywistych w taki sposób, że miara dowolnego odcinka jest dodatnia i skończona oraz przesuwając zbiór na prostej, nie zmieniamy jego miary (uzasadnienie na marginesie). Ważne jest zatem, aby definiując miarę, zaznaczyć, jaka jest jej dziedzina, czyli jakie zbiory są względem niej mierzalne.
Jak w takim razie możemy zdefiniować miarę - poza trywialnym przypadkiem miary liczącej, która podzbiorom zbioru przeliczalnego przyporządkowuje liczbę elementów? Z pomocą przychodzi nam pojęcie miary zewnętrznej. Jest to nieujemna funkcja  określona na wszystkich podzbiorach danej przestrzeni, która spełnia warunki: (a)
określona na wszystkich podzbiorach danej przestrzeni, która spełnia warunki: (a) 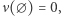 (b) jeśli
(b) jeśli 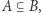 to
to 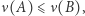 (c) miara zewnętrzna "połączenia" dowolnie wielu zbiorów (niekoniecznie rozłącznych) jest nie większa od sumy miar zewnętrznych tych zbiorów. Jeśli znajdziemy miarę zewnętrzną (warunki są łagodniejsze od tych, które definiują miarę!), to możemy zapytać o zbiory
(c) miara zewnętrzna "połączenia" dowolnie wielu zbiorów (niekoniecznie rozłącznych) jest nie większa od sumy miar zewnętrznych tych zbiorów. Jeśli znajdziemy miarę zewnętrzną (warunki są łagodniejsze od tych, które definiują miarę!), to możemy zapytać o zbiory 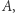 które są dobrymi "rozdzielnikami", to znaczy dla dowolnego podzbioru
które są dobrymi "rozdzielnikami", to znaczy dla dowolnego podzbioru 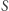 badanej przestrzeni zachodzi
badanej przestrzeni zachodzi 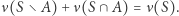 Mówimy wówczas, że zbiór
Mówimy wówczas, że zbiór 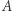 spełnia warunek Carathéodory'ego względem
spełnia warunek Carathéodory'ego względem  Okazuje się, że jeśli ograniczymy
Okazuje się, że jeśli ograniczymy  do zbiorów spełniających warunek Carathéodory'ego względem niej, to otrzymamy miarę (jak już wspomnieliśmy, określenie dziedziny przy definiowaniu miary jest bardzo istotne!).
do zbiorów spełniających warunek Carathéodory'ego względem niej, to otrzymamy miarę (jak już wspomnieliśmy, określenie dziedziny przy definiowaniu miary jest bardzo istotne!).
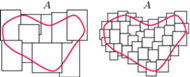
Coraz dokładniejsze pokrycia zbioru 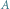 prostymi prostokątami dają coraz lepsze przybliżenie jego miary zewnętrznej
prostymi prostokątami dają coraz lepsze przybliżenie jego miary zewnętrznej 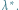
Uf, zrobiło się bardzo abstrakcyjnie - zobaczmy, jak to działa na przykładzie. Co to jest pole powierzchni, każdy widzi, ale mało kto potrafiłby je zdefiniować w sposób zadowalający matematyka (Czytelniku, jeśli nie wiesz jak, spróbuj przez chwilę uczynić to sam!). Zacznijmy od zdefiniowania pola prostokąta o bokach równoległych do osi ustalonego układu współrzędnych (taki prostokąt nazwiemy "prostym"). Dla prostego prostokąta ![|[a1,b1] ×[a2,b2]](/math/temat/matematyka/analiza/teoria_miary/2019/05/26/Miara/1x-4c57fbe1bd2269d6a85979f5887c6de68603a58f-im-33,33,33-FF,FF,FF.gif) określamy pole zgodnie z naszymi oczekiwaniami, czyli
określamy pole zgodnie z naszymi oczekiwaniami, czyli 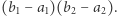 Dla dowolnie ustalonego podzbioru płaszczyzny
Dla dowolnie ustalonego podzbioru płaszczyzny 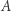 rozważmy teraz wszystkie możliwe jego pokrycia przeliczalną liczbą prostych prostokątów, a dla każdego takiego pokrycia zsumujmy pola tych prostokątów. Kres dolny (czyli największe ograniczenie dolne) tych sum oznaczmy jako
rozważmy teraz wszystkie możliwe jego pokrycia przeliczalną liczbą prostych prostokątów, a dla każdego takiego pokrycia zsumujmy pola tych prostokątów. Kres dolny (czyli największe ograniczenie dolne) tych sum oznaczmy jako 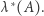 Można udowodnić, że
Można udowodnić, że 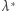 jest miarą zewnętrzną na płaszczyźnie. Jeśli więc ograniczymy ją do zbiorów, które spełniają względem niej warunek Carathéodory'ego, dostaniemy miarę nazywaną dwuwymiarową miarą Lebesgue'a - i to jest dla matematyka porządnie zdefiniowane pole. Oczywiście, należałoby się jeszcze zastanowić, jakie właściwie zbiory są mierzalne względem miary Lebesgue'a (warunek Carathéodory'ego nie jest bowiem szczególnie wygodny). Jedna z charakteryzacji mówi, że są to zbiory będące złączeniem co najwyżej przeliczalnej liczby zbiorów domkniętych oraz zbioru, którego miara zewnętrzna
jest miarą zewnętrzną na płaszczyźnie. Jeśli więc ograniczymy ją do zbiorów, które spełniają względem niej warunek Carathéodory'ego, dostaniemy miarę nazywaną dwuwymiarową miarą Lebesgue'a - i to jest dla matematyka porządnie zdefiniowane pole. Oczywiście, należałoby się jeszcze zastanowić, jakie właściwie zbiory są mierzalne względem miary Lebesgue'a (warunek Carathéodory'ego nie jest bowiem szczególnie wygodny). Jedna z charakteryzacji mówi, że są to zbiory będące złączeniem co najwyżej przeliczalnej liczby zbiorów domkniętych oraz zbioru, którego miara zewnętrzna 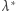 wynosi 0. Brzmi bardzo skomplikowanie, ale oznacza między innymi, że możemy śmiało mierzyć pola wszystkich figur geometrycznych znanych ze szkoły średniej. I jak tu nie wierzyć w słowa Goethego:
wynosi 0. Brzmi bardzo skomplikowanie, ale oznacza między innymi, że możemy śmiało mierzyć pola wszystkich figur geometrycznych znanych ze szkoły średniej. I jak tu nie wierzyć w słowa Goethego:
Matematycy są jak Francuzi: cokolwiek im się powie, od razu przekładają to na swój własny język i wówczas staje się to zupełnie czymś innym.
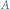 prostymi prostokątami dają coraz lepsze przybliżenie jego miary zewnętrznej
prostymi prostokątami dają coraz lepsze przybliżenie jego miary zewnętrznej