O kul rozmnażaniu

Paradoks Banacha-Tarskiego (1924 r.). Kulę można rozłożyć na skończenie wiele części, z których da się zbudować dwie takie same kule.

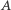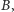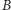Rozkład w używanym tu sensie to dowolny podział figury na rozłączne części (niekoniecznie ma ich być skończenie wiele). Dopuszczamy zatem części o dowolnie dziwnych kształtach, na przykład jednopunktowe lub niemierzalne. Jeśli figurę $A$ możemy rozłożyć w tym sensie na części, z których następnie można złożyć figurę $B, |$ to mówimy, że $A$ i $B |$ są równoważne przez rozkład i oznaczamy to 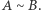$A ∼ B.$ Nietrudno sprawdzić, że rzeczywiście jest to relacja równoważności. Okazuje się, że takie podziały nie muszą zachowywać miar figur i stąd właśnie biorą się pozorne paradoksy, a dokładniej mówiąc, fakty sprzeczne z naszą intuicją.

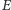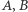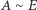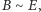Zbiór $E$ jest paradoksalny , jeśli zawiera rozłączne podzbiory $A, B$ takie, że $A ∼ E$ oraz $B ∼ E,$ czyli, mówiąc obrazowo, jeśli z pewnych dwóch rozłącznych części zbioru możemy zbudować dwie jego pełnowartościowe kopie. Chodzi więc o takie rozkłady, które są sprzeczne z naszą intuicją dotyczącą pola lub objętości. W dalszej części tekstu rozważamy tylko rozkłady skończone.

Po wyjaśnieniu, na czym polega problem, kolej na wskazanie narzędzi - będą właściwie dwa: łatanie dziur i grupa wolna.

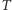Łatanie dziur pokażemy na przykładzie dziury w okręgu. Rozłożymy okrąg $|S1$ bez punktu na dwie części, zastosujemy do nich odpowiednio dobrane obroty i w rezultacie uzyskamy cały okrąg. Niech $|T$ będzie brakującym punktem okręgu, 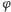$|φ$ zaś niech będzie obrotem wokół środka o ustalony kąt niewspółmierny z 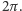$2π.$ Wówczas ciąg 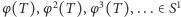$|φ(T ),φ2(T),φ 3(T),...∈ S1$ jest nieskończony i są to różne punkty. Niech to będzie pierwszy z naszych dwóch zbiorów, a pozostała część okręgu niech będzie drugim. Zauważmy, że obrót w przeciwną stronę o ten sam kąt, czyli 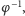$φ−1,$ przeprowadza powyższy ciąg na ciąg 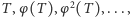$T ,φ(T ),φ2(T ),...,$ a więc pozwala załatać dziurkę. Pozostała część okręgu jest nieruchoma (to też obrót). Stąd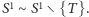 $1 1 |S ∼ S ∖ {T }.$

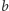Grupa wolna $F 2$ o dwóch generatorach $|a$ i $b$ to zbiór słów (czyli skończonych ciągów znaków) nad alfabetem $−1 −1 a, b,a ,b ,$ zredukowanych (czyli bez fragmentów postaci $xx −1$ ), z elementem neutralnym $e$ (słowo puste), bez relacji (dwa zredukowane słowa o różnym zapisie są różne) i z działaniem konkatenacji (dopisywania). 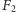Zauważmy, że ponieważ rozpatrujemy tylko słowa skończone, grupa $|F2$ ma przeliczalnie wiele elementów. Rysuje się je często jako wierzchołki grafu (rysunek). Taki graf nie ma cykli, ponieważ w grupie wolnej nie ma relacji.

Niech 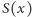$S(x)$ oznacza zbiór słów zaczynających się literą 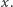$|x.$ Zauważmy, że 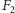$|F2$ jest rozłączną sumą

{e} ∪ S(a) ∪S(b) ∪ S(a −1) ∪S(b −1).

Jednocześnie

F = S(a)∪ aS(a −1) oraz F = S(b) ∪ bS(b −1). 2 2

Grupa wolna 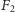$|F2$ jest zatem paradoksalna (dopisanie słowa na początku drugiego słowa to działanie grupy 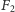$F 2$ na zbiorze swoich elementów).

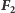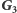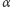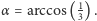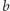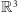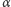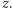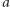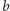Wolną podgrupę $F2$ możemy znaleźć w grupie $G3$ izometrii przestrzeni trójwymiarowej. Konkretnie, niech $α$ będzie kątem dwuściennym czworościanu foremnego, czyli $1 α = arccos(3) .$ Niech $|a$ oraz $b$ będą obrotami $|R3$ o kąt $α$ w odpowiednio dobranym kierunku i odpowiednio wokół osi $|x$ oraz $z.$ Można sprawdzić, że takie $a$ i $b$ generują grupę wolną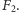 $|F2.$

Od grupy do zbioru. Umiemy wykazać, że 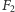$|F2$ jest paradoksalna i umiemy wskazać podgrupę 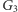$G3$ izomorficzną z 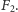$F2. |$ Docelowo chcielibyśmy jednak skonstruować nie grupę, lecz zbiór paradoksalny.

Okazuje się, że paradoksalność grupy daje się przenieść na zbiór, na którym ta grupa działa. Prześledźmy tę ogólną prawidłowość na przykładzie działania grupy 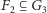$F2| ⊆ G3$ na sferę 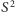$S2 |$ (o środku w początku układu współrzędnych) z wyłączonym zbiorem 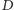$|D$ tych punktów, w których osie obrotów, z jakich się składa $|F2,$ przebijają tę sferę.

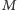Zbiór $S2 ∖D$ rozpada się na orbity przy działaniu $F2. |$ Wybierzmy (tu działa pewnik wyboru i bez niego ani rusz) zbiór $M |$ reprezentantów tych orbit i zastosujmy do niego grupę $F2. |$ Zauważmy, że tak otrzymane przeliczalnie wiele rozłącznych obrazów zbioru $M$ daje w sumie całe $|S2∖ D.$ Odpowiednio je grupując i przemieszczając, uzyskujemy paradoksalny rozkład $2 S| ∖ D.$

Grupa wolna już swoją rolę odegrała, pora na łatanie dziur. Jak już zauważyliśmy, grupa 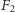$F2 |$ jest przeliczalna, a każda oś obrotu przebija sferę w dwóch punktach, stąd zbiór 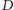$D$ również jest przeliczalny. Stosując opisaną wyżej metodę łatania dziur, można wykazać, że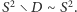 $|S2∖ D ∼S2.$

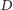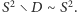Dokończenie dowodu paradoksu Banacha-Tarskiego. Wiemy już, że dla odpowiednio dobranego zbioru $D$ zbiór $2 S | ∖ D$ jest paradoksalny, oraz że $|S2∖ D ∼S2.$ Ponieważ zbiór równoważny ze zbiorem paradoksalnym też jest paradoksalny, więc sfera jest paradoksalna.

Zauważmy, że kula bez środka to "cebulka" złożona ze sfer współśrodkowych. Skoro każda z nich jest paradoksalna, to kula bez środka również jest paradoksalna (bo punkty każdego promienia możemy skleić i przemieszczać wspólnie).

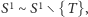Weźmy teraz dowolny okrąg przechodzący przez środek kuli $|T$ i całkowicie w niej zawarty. Wiemy, że $1 1 S ∼S ∖{T },$ zatem umiemy załatać dziurkę, czyli kula bez środka jest równoważna całej kuli. A to kończy dowód, że kula jest paradoksalna.

***

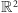O tym, że powyższą metodą nie można uzyskać analogicznych paradoksalnych rozkładów w $R1$ ani w $R2$ łatwo się przekonać, sprawdzając, że 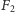$F2$ nie jest podgrupą grupy 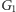$G1$ izometrii prostej ani grupy $G2$ izometrii płaszczyzny. Przyjrzyjmy się dokładniej, dlaczego tak jest.

Izometrie prostej to przesunięcia i symetrie względem punktu. Wobec tego kwadrat każdej izometrii jest przesunięciem, przesunięcia zaś są przemienne. Stąd dla dowolnych dwóch izometrii 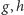$g, | h$ zachodzi relacja 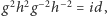$2 2 −2 −2 g h g h = id,$ czyli w 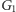$G1$ nie ma podgrupy wolnej rzędu 2.

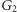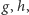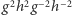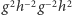Na płaszczyźnie każda izometria jest złożeniem co najwyżej trzech symetrii osiowych (twierdzenie Chaslesa - jego dowód można znaleźć np. w Delcie 11/2015). Wynika z tego, że kwadraty elementów $G2 |$ to izometrie parzyste, a więc przesunięcia lub obroty. Wobec tego dla dowolnych dwóch izometrii $|g,h,$ złożenia $2 2 −2 −2 g h g h$ oraz $2 −2 −2 2 g h g h$ są przesunięciami (bo kąty ewentualnych obrotów się redukują). Przesunięcia są przemienne, zatem

2 2 −2 −2 2 −2 −2 2 2 2 −2 −2 −1 2 −2 −2 2 −1 (g h g h )(g h g h )(g h g h ) (g h g h ) = id,

co po uproszczeniu daje relację

g2h2g −2h −2g2h −2g −2h4g2h −2g−2h−2g2h2g−2 = id,

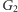czyli w $G2$ także nie ma podgrupy wolnej rzędu 2.

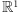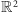Ale innej metody na znalezienie paradoksalnych rozkładów w $1 R |$ i $2 R$ nie ma, albowiem Stefan Banach udowodnił, że podane wyżej tożsamości pociągają za sobą istnienie miary uniwersalnej , czyli mierzącej wszystkie zbiory i będącej rozszerzeniem zwykłego mierzenia długości czy pola. Bo przecież zbiory paradoksalne nie mogą mieć miary w zwykłym sensie, o czym, jak sądzę, nikogo przekonywać nie trzeba.