Zadanie ZM-1558
o zadaniu...
- Publikacja w Delcie: marzec 2018
- Publikacja elektroniczna: 28 lutego 2018
Czy istnieją liczby całkowite 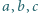 o tej własności, że każdy z trójmianów kwadratowych
o tej własności, że każdy z trójmianów kwadratowych
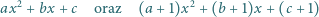
ma obydwa pierwiastki całkowite?
Czy istnieją liczby całkowite 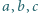 o tej własności, że każdy z trójmianów kwadratowych
o tej własności, że każdy z trójmianów kwadratowych
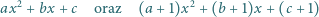
ma obydwa pierwiastki całkowite?
Niech 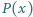 będzie takim wielomianem o współczynnikach rzeczywistych, że
będzie takim wielomianem o współczynnikach rzeczywistych, że
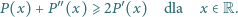
Dowieść, że 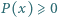 dla
dla 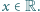
Jednym z pierwiastków wielomianu 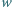 o współczynnikach całkowitych jest liczba
o współczynnikach całkowitych jest liczba 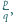 gdzie
gdzie 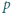 i
i 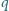 są względnie pierwszymi liczbami całkowitymi. Wykazać, że liczba
są względnie pierwszymi liczbami całkowitymi. Wykazać, że liczba 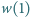 jest podzielna przez
jest podzielna przez 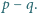
Liczby 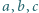 są rozwiązaniami równania
są rozwiązaniami równania 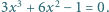 Obliczyć wartość
Obliczyć wartość
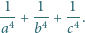
Zadanie 6 pochodzi z LXIV Olimpiady Matematycznej, a opisane tu rozwiązanie przedstawił jej uczestnik.
Czy istnieje wielomian o współczynnikach całkowitych, który nie jest różnowartościowy na zbiorze liczb rzeczywistych, ale jest różnowartościowy na zbiorze liczb wymiernych?
Zadanie 706 zaproponował pan Witold Bednarek z Łodzi.
Wyznaczyć wszystkie liczby naturalne 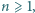 dla których istnieje wielomian
dla których istnieje wielomian 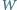 stopnia
stopnia 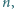 o współczynnikach całkowitych, ze współczynnikiem wiodącym równym 1, i taki, że równanie
o współczynnikach całkowitych, ze współczynnikiem wiodącym równym 1, i taki, że równanie 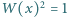 ma
ma 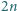 pierwiastków całkowitych (niekoniecznie różnych).
pierwiastków całkowitych (niekoniecznie różnych).
Niech 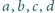 będą takimi liczbami rzeczywistymi, że
będą takimi liczbami rzeczywistymi, że

Wykazać, że 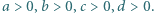
Udowodnić, że liczba

jest niewymierna.
Rozważmy zbiór

złożony z 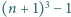 punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór
punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór 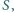 ale nie zawiera punktu
ale nie zawiera punktu 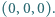
Niech 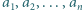 oraz
oraz 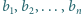 będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci
będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci 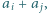 gdzie
gdzie 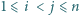 pokrywa się z zestawem
pokrywa się z zestawem 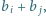 dla
dla 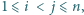 to
to 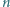 jest potęgą liczby 2.
jest potęgą liczby 2.
Liczby rzeczywiste 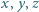 spełniają warunki
spełniają warunki

Udowodnić, że 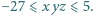
Dane jest 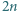 parami różnych liczb rzeczywistych
parami różnych liczb rzeczywistych 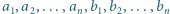 oraz tablica
oraz tablica 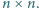 W pole leżące w
W pole leżące w 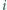 -tym wierszu i w
-tym wierszu i w 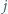 -tej kolumnie wpisano liczbę
-tej kolumnie wpisano liczbę 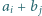 dla
dla 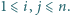 Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.
Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.
Znaleźć wszystkie pary wielomianów rzeczywistych 
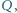 spełniające równanie
spełniające równanie
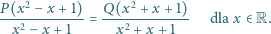
Niech 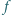 będzie wielomianem stopnia
będzie wielomianem stopnia 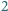 o całkowitych współczynnikach. Wiadomo, że
o całkowitych współczynnikach. Wiadomo, że 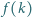 jest podzielne przez
jest podzielne przez 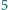 dla każdej liczby całkowitej
dla każdej liczby całkowitej 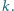 Udowodnić, że wówczas każdy współczynnik
Udowodnić, że wówczas każdy współczynnik 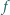 jest podzielny przez
jest podzielny przez 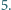
Niech 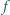 będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli
będzie wielomianem o współczynnikach całkowitych o stopniu co najmniej 1. Wykaż, że jeśli  i
i 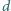 są różnymi liczbami całkowitymi, to
są różnymi liczbami całkowitymi, to  dzieli
dzieli 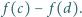
Zbadaj, czy istnieje taki wielomian 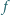 stopnia 3 o współczynnikach całkowitych, że
stopnia 3 o współczynnikach całkowitych, że 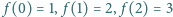 oraz
oraz 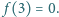
Zadanie 666 zaproponował pan Witold Bednarek z Łodzi.
Niech
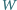 będzie wielomianem stopnia
będzie wielomianem stopnia
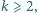 o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
o współczynnikach
całkowitych nieujemnych. Zakładamy, że dla każdej liczby naturalnej
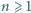 wartość
wartość
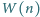 jest
jest
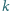 -tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
-tą potęgą liczby całkowitej
nieujemnej. Udowodnić, że
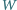 ma postać
ma postać
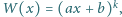 gdzie
gdzie
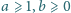 są liczbami całkowitymi.
są liczbami całkowitymi.
Niech wielomian
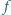 postaci
postaci
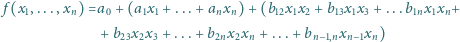
przyjmuje na zbiorze
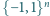 tylko dwie wartości
tylko dwie wartości
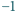 lub
lub
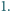 Udowodnić, że suma kwadratów jego współczynników wynosi
Udowodnić, że suma kwadratów jego współczynników wynosi
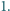
Wielomian
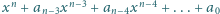 ma współczynniki
rzeczywiste
ma współczynniki
rzeczywiste
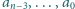 nie wszystkie równe
nie wszystkie równe
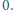 Udowodnić, że
ma on mniej niż
Udowodnić, że
ma on mniej niż
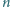 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
Dany jest wielomian
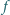 o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
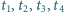 , że
, że

Udowodnić, że nie istnieje liczba całkowita
 , dla której
, dla której
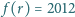 .
.