Zadanie ZM-1342
o zadaniu...
- Publikacja w Delcie: marzec 2012
- Publikacja elektroniczna: 02-03-2012
Mówimy, że funkcja
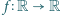 ma cykl długości
ma cykl długości
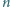 o początku
o początku
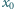 , gdy istnieje takie
, gdy istnieje takie
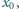 że liczby
że liczby
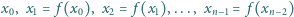 są parami różne, zaś
są parami różne, zaś
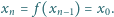
Udowodnić, że jeśli wielomian o współczynnikach całkowitych ma
cykl o początku będącym liczbą całkowitą, to jest on długości
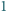 lub
lub
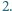
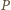 o współczynnikach
całkowitych ma cykl
o współczynnikach
całkowitych ma cykl
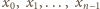 długości
długości
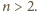 Mamy
Mamy
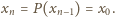 Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
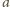 i
i
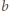 zachodzi
zachodzi
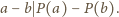
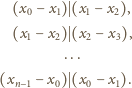
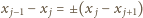
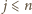 (przyjmujemy, że
(przyjmujemy, że
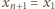 ). Znak „–” jest
wykluczony, gdyż liczby
). Znak „–” jest
wykluczony, gdyż liczby
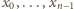 są parami różne. Mamy więc
są parami różne. Mamy więc
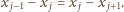 Oznacza to, że ciąg
Oznacza to, że ciąg
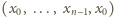 jest
arytmetyczny. Musi on być stały, co daje sprzeczność.
jest
arytmetyczny. Musi on być stały, co daje sprzeczność.
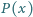 będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
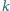 istnieje taka
liczba całkowita
istnieje taka
liczba całkowita
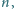 że liczba
że liczba
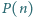 ma co najmniej
ma co najmniej
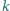 różnych dzielników pierwszych.
różnych dzielników pierwszych.
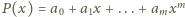 (
(
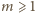 ).
).
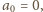 wystarczy wziąć dowolną liczbę
wystarczy wziąć dowolną liczbę
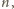 będącą iloczynem
będącą iloczynem
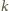 różnych liczb pierwszych. Są one oczywiście dzielnikami liczby
różnych liczb pierwszych. Są one oczywiście dzielnikami liczby
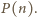 Dalej przyjmijmy, że
Dalej przyjmijmy, że
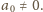
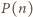 jest nieskończony. Przypuśćmy bowiem, że jest to zbiór
skończony
jest nieskończony. Przypuśćmy bowiem, że jest to zbiór
skończony
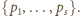 Biorąc jako
Biorąc jako
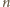 dowolną liczbę postaci
dowolną liczbę postaci
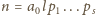 (
(
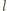 całkowite), mamy
całkowite), mamy
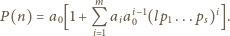
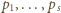 (a swoboda wyboru
(a swoboda wyboru
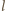 pozwala przyjąć, że jest różna
od
pozwala przyjąć, że jest różna
od
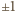 ); ma więc jakiś inny dzielnik pierwszy, wbrew uczynionemu
przypuszczeniu.
); ma więc jakiś inny dzielnik pierwszy, wbrew uczynionemu
przypuszczeniu.
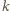 istnieją różne liczby pierwsze
istnieją różne liczby pierwsze
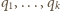 oraz takie liczby całkowite
oraz takie liczby całkowite
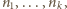 że
że
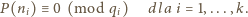
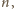 spełniającą układ kongruencji
spełniającą układ kongruencji

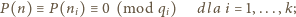
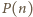 ma więc co najmniej
ma więc co najmniej
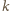 różnych dzielników
pierwszych.
różnych dzielników
pierwszych.
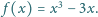 Definiujemy indukcyjnie
Definiujemy indukcyjnie
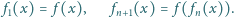
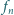 ma
ma
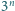 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
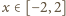 możemy napisać
możemy napisać
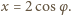
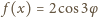
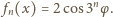
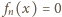 dla
dla
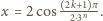 Ponieważ
funkcja
Ponieważ
funkcja
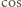 jest malejąca w przedziale
jest malejąca w przedziale
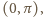 więc pierwiastki
otrzymane dla
więc pierwiastki
otrzymane dla
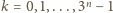 będą różne, a więcej pierwiastków
będą różne, a więcej pierwiastków
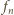 mieć nie może.
mieć nie może.