Wielomiany, nierówności i Newton
Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...
Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...
Algebra Kącik początkującego olimpijczyka
O licznych zastosowaniach faktu, że dla każdego wielomianu 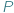 w sumie algebraicznej
w sumie algebraicznej 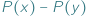 można wyłączyć przed nawias wyrażenie
można wyłączyć przed nawias wyrażenie 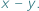
Algebra Kącik początkującego olimpijczyka
O stosowaniu podstawowej wiedzy szkolnej na temat funkcji kwadratowej do rozwiązywania zadań olimpijskich.
Suma kwadratów najczęściej kojarzy się nam z twierdzeniem Pitagorasa - słusznie, ale warto wiedzieć, że temat ten ma swoje miejsce również w teorii liczb, gdzie interesuje nas, czy daną liczbę całkowitą można przedstawić w postaci sumy kwadratów innych liczb całkowitych. Intrygujące jest również pytanie, ile składników znajduje się w tej sumie. Osiągnięcia w tym zakresie mieli między innymi Fermat, Euler i Lagrange...

Poniższa opowieść była na tyle ważna dla młodego, zaledwie dwudziestoletniego, matematyka Évariste'a Galois, że poświęcił ostatni dzień przed pojedynkiem, aby spisać ją w liście do przyjaciela. Niestety, nie dostał od losu szansy na kontynuowanie swoich prac, ale jakiś czas po jego śmierci matematycy zrozumieli znaczenie jego pomysłów. Ślady teorii, z której zarysem Czytelnik zapoznać się może w dalszej części artykułu, odnaleźć można w wielu gałęziach współczesnej matematyki. Jej bezpośrednim następstwem jest wiele efektownych rozwiązań problemów, których ludzkość szukała przez setki lat: nierozwiązalność (przez pierwiastniki) równań wielomianowych stopnia 5 lub wyższego, niekonstruowalność pewnych wielokątów foremnych (cyrklem i linijką), a także niewykonalność klasycznych konstrukcji geometrycznych, czyli podwojenia sześcianu, trysekcji kąta i kwadratury koła.
W Delcie 7/2017 przedstawiliśmy kilka "olimpijskich" zastosowań twierdzenia Combinatorial Nullstellensatz. Okazuje się, że zamiast "zwykłych" wielomianów wielu zmiennych możemy rozważać wielomiany o współczynnikach będących resztami z dzielenia przez pewną liczbę pierwszą 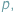 z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo 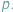 Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
Zadanie 6 z 48. Międzynarodowej Olimpiady Matematycznej (IMO) z 2007 roku było jednym z najtrudniejszych w historii Międzynarodowej Olimpiady Matematycznej.

Dlaczego w szkole tak dużo uczymy się o wielomianach? Są dwa podstawowe powody. Pierwszy z nich - całkiem zrozumiały - po prostu jest to niemal największa klasa funkcji, których wartości umiemy obliczać. Potrafimy jeszcze dzielić wartości wielomianów, ale z pozostałymi funkcjami, które występują w programie szkolnym, a później na studiach, w zasadzie mielibyśmy sporo problemów.

Paolo Ruffini (1765-1822)
Równania algebraiczne, czyli takie, które można zapisać, przyrównując wielomian do zera, intrygowały ludzi od bardzo dawna. Rozwiązywaniem równań zajmowano się już w czasach starożytnych. W szkole uczą nas, jak rozwiązywać równania liniowe i kwadratowe, to jest takie, w których występuje funkcja liniowa (wielomian stopnia pierwszego) albo funkcja kwadratowa (wielomian stopnia drugiego). Matematycy włoscy podali w XVI wieku wzory na pierwiastki równań stopnia trzeciego i czwartego. A co z równaniami wyższych stopni?
Dotarliśmy do ostatniej części cyklu, w którym prezentujemy wybrane przykłady zaskakujących relacji pomiędzy różnymi, pozornie bardzo odległymi, obszarami matematyki. Nie wypada jednak zakończyć bez poświęcenia należytej uwagi dziedzinie teorii liczb. Jak bowiem matematyka nazywana jest często królową nauk, tak o teorii liczb mówi się często jako o królowej matematyki. A królowa ma, oczywiście, wielu służących.
Rozważamy wielomian 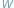 o współczynnikach rzeczywistych stopnia
o współczynnikach rzeczywistych stopnia 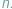 Wiadomo, że wielomian taki ma
Wiadomo, że wielomian taki ma 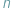 pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu
pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu 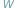 należących do wybranego przedziału
należących do wybranego przedziału 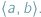 Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej
Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej 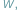 znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.
znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.
Poniższe zadania łączy to, że do rozwiązania każdego z nich można użyć pewnego Bardzo Znanego Twierdzenia, udowodnionego całkiem niedawno. Oczywiście to, że można strzelać z armaty do muchy nie oznacza, że zawsze trzeba...
Rozważamy wielomian  stopnia
stopnia 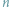 o współczynnikach rzeczywistych...
o współczynnikach rzeczywistych...
Jednomiany postaci 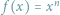 są jednymi z pierwszych funkcji rzeczywistych, z którymi mamy do czynienia w naszym matematycznym życiu. Odrobinę później poznajemy ich kombinacje o współczynnikach rzeczywistych, czyli tytułowe wielomiany. Jest więc to pojęcie elementarne, które powinno być doskonale znane każdemu maturzyście. Tym bardziej może zadziwiać, jak często wielomiany i ich podstawowe własności stanowią klucz do wielu trudnych problemów, które na pozór nic z wielomianami wspólnego nie mają. Zaprezentujemy to na przykładach z algebry, teorii liczb i kombinatoryki.
są jednymi z pierwszych funkcji rzeczywistych, z którymi mamy do czynienia w naszym matematycznym życiu. Odrobinę później poznajemy ich kombinacje o współczynnikach rzeczywistych, czyli tytułowe wielomiany. Jest więc to pojęcie elementarne, które powinno być doskonale znane każdemu maturzyście. Tym bardziej może zadziwiać, jak często wielomiany i ich podstawowe własności stanowią klucz do wielu trudnych problemów, które na pozór nic z wielomianami wspólnego nie mają. Zaprezentujemy to na przykładach z algebry, teorii liczb i kombinatoryki.
Matematyka, zwłaszcza tzw. szkolna, wypracowała przez lata procedury rozwiązywania określonego typu zadań. Gdy rozpoznajemy problem jako równanie kwadratowe, w głowie pojawia się hasło "bekwadratminusczteryace" i już wszystko wiadomo, niezależnie od tego, jak w rzeczywistości nazwaliśmy współczynniki funkcji kwadratowej...
Rozwiąż równanie! – to jedno z najczęściej słyszanych przez ucznia poleceń nauczyciela matematyki. Gdy usłyszymy to polecenie, nie wątpimy, że otrzymane równanie można rozwiązać i że my potrafimy to zrobić. Zresztą o każdym zadaniu matematycznym, na które natrafimy, uważamy, że można je rozwiązać. Jeśli nie widzimy rozwiązania od razu, to pewnie trzeba jeszcze trochę pomyśleć, pokombinować, wynaleźć jakiś sprytny sposób, może poczytać w mądrych książkach i rozwiązanie musi się znaleźć. Czy na pewno tak jest? Okazuje się, że istnieją zadania, niedające się rozwiązać, choć są łudząco podobne do innych, które rozwiązujemy bez trudu.
Za pomocą kolorowania wielomianów można udowodnić Zasadnicze twierdzenie algebry w zaskakująco elementarny sposób...
Każdy uczeń szkoły średniej wie, że gdy zna się współczynniki trójmianu kwadratowego, to można jawnymi wzorami wyrazić pierwiastki tego trójmianu. We wzorach tych wykonuje się (skończoną liczbę razy) tylko cztery działania arytmetyczne i pierwiastkowanie.
Jak wiele innych ważnych twierdzeń matematyki, zasadnicze twierdzenie algebry,
udowodnione przez Carla Friedricha Gaussa w ostatnim roku osiemnastego stulecia,
informuje nas, że pewne obiekty nie istnieją. Mianowicie, nie ma takiego, różnego od
stałej, wielomianu zmiennej zespolonej, który nie znikałby w żadnym punkcie
płaszczyzny zespolonej