Z tożsamości
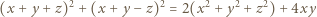
wynika, że zadane równanie jest równoważne następującemu:
 |
(1) |
Jest też równoważne każdemu z dwóch równań uzyskanych przez cykliczne przestawienie zmiennych w (1). Jeśli więc liczby całkowite 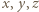 spełniają warunki zadania, to iloczyny
spełniają warunki zadania, to iloczyny 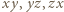 są nieujemne, co oznacza, że liczby
są nieujemne, co oznacza, że liczby 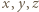 są wszystkie nieujemne lub wszystkie niedodatnie.
są wszystkie nieujemne lub wszystkie niedodatnie.
Weźmy przypadek, gdy 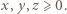 Ze związku (1) (oraz warunku, że
Ze związku (1) (oraz warunku, że 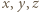 nie mają wspólnego dzielnika
nie mają wspólnego dzielnika 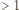 ) wynika, że
) wynika, że 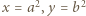 dla pewnej pary liczb całkowitych
dla pewnej pary liczb całkowitych 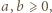 względnie pierwszych. Przepisujemy (1) jako
względnie pierwszych. Przepisujemy (1) jako 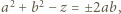 czyli
czyli 
Uwzględniając pominięty przypadek, gdy 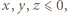 widzimy, że trójka
widzimy, że trójka 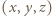 ma postać
ma postać
 |
(2) |
Na odwrót, jeśli trójka liczb całkowitych 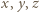 ma taką postać (więc
ma taką postać (więc 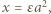
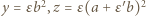 ;
; 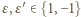 ), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby
), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby 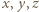 są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.
są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.
Można sformułować tę odpowiedź w formie bardziej symetryczej, pisząc, że liczby 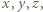 po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych
po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych
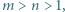 przy czym
przy czym 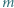 jest liczbą parzystą. Udowodnić, że równanie
jest liczbą parzystą. Udowodnić, że równanie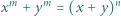
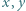 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 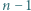 dzieli się przez
dzieli się przez 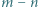 .
.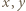 spełniają podane równanie. Oznaczmy przez
spełniają podane równanie. Oznaczmy przez 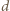 ich największy wspólny dzielnik; tak więc
ich największy wspólny dzielnik; tak więc 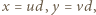 gdzie
gdzie 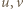 to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez
to liczby naturalne względnie pierwsze. Wstawiając to do równania i dzieląc stronami przez 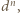 otrzymujemy
otrzymujemy
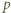 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 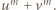 Wobec związku (1)
Wobec związku (1) 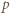 jest też dzielnikiem sumy
jest też dzielnikiem sumy 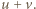 To znaczy, że
To znaczy, że 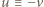 (mod
(mod 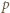 ); a skoro
); a skoro 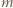 jest liczbą parzystą, mamy stąd
jest liczbą parzystą, mamy stąd 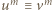 (mod
(mod 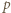 ), i dalej
), i dalej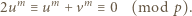
 nie dzieli się przez
nie dzieli się przez 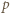 (bo
(bo 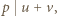 zaś
zaś 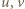 są względnie pierwsze); zatem
są względnie pierwsze); zatem 
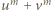 nie ma innych dzielników pierwszych, znaczy to, że
nie ma innych dzielników pierwszych, znaczy to, że
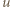 i
i  (względnie pierwsze) są obie nieparzyste; stąd
(względnie pierwsze) są obie nieparzyste; stąd 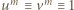 (mod 4), bo
(mod 4), bo 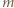 jest liczbą parzystą. W równości (2) mamy więc
jest liczbą parzystą. W równości (2) mamy więc 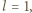 skąd
skąd 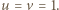 Wracamy do równania (1):
Wracamy do równania (1): 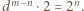 To pokazuje, że
To pokazuje, że 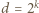 (dla pewnego
(dla pewnego 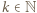 ); przy tym
); przy tym 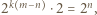 czyli
czyli 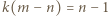 : liczba
: liczba 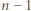 dzieli się przez
dzieli się przez 
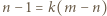 dla pewnego
dla pewnego 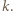 Wówczas para
Wówczas para 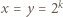 jest rozwiązaniem zadanego równania:
jest rozwiązaniem zadanego równania: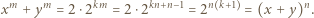
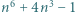 jest złożona dla każdej liczby całkowitej dodatniej
jest złożona dla każdej liczby całkowitej dodatniej 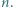
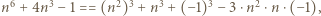 i użyć tożsamości (2) z artykułu dla
i użyć tożsamości (2) z artykułu dla 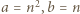 i
i 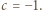
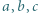 są całkowite. Wykazać, że jeśli liczba
są całkowite. Wykazać, że jeśli liczba 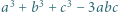 dzieli się przez 3, to dzieli się ona również przez 9.
dzieli się przez 3, to dzieli się ona również przez 9.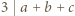 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 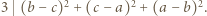 To ma miejsce dokładnie wtedy, gdy liczby
To ma miejsce dokładnie wtedy, gdy liczby 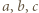 dają trzy jednakowe albo trzy różne reszty z dzielenia przez 3.
dają trzy jednakowe albo trzy różne reszty z dzielenia przez 3.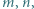 przy czym
przy czym 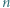 jest liczbą nieparzystą, większą niż
jest liczbą nieparzystą, większą niż 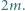 Udowodnić, że liczba
Udowodnić, że liczba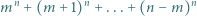
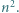
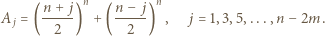
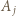 dzieli się przez
dzieli się przez 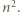 W rozwinięciu dwumianowym
W rozwinięciu dwumianowym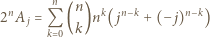
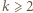 są podzielne przez
są podzielne przez 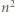 ; skoro zaś
; skoro zaś 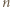 jest liczbą nieparzystą, dwa składniki początkowe dają w sumie
jest liczbą nieparzystą, dwa składniki początkowe dają w sumie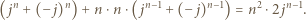
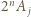 dzieli się przez
dzieli się przez 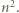 Korzystając jeszcze raz z nieparzystości
Korzystając jeszcze raz z nieparzystości 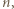 wnosimy, że
wnosimy, że 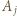 dzieli się przez
dzieli się przez 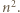
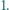 Jeśli na tablicy napisana jest co najmniej jedna z liczb
Jeśli na tablicy napisana jest co najmniej jedna z liczb 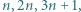 to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy.
to można dopisać każdą z pozostałych. Rozstrzygnąć, czy każda dodatnia liczba całkowita może w pewnym momencie pojawić się na tablicy. mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie.
mogła zostać uzyskana (poprzez ciąg kilku kolejnych dopisywań) z pewnej mniejszej liczby. Stąd dostaniemy odpowiedź twierdzącą na postawione w zadaniu pytanie. z dzielenia przez
z dzielenia przez 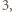 powiedzmy
powiedzmy 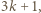 można uzyskać w jednym kroku z liczby
można uzyskać w jednym kroku z liczby 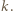 Liczba dająca resztę
Liczba dająca resztę 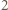 z dzielenia przez
z dzielenia przez 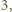 powiedzmy
powiedzmy 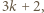 może zostać uzyskana w dwóch krokach z liczby
może zostać uzyskana w dwóch krokach z liczby 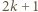 : w pierwszym kroku dopisujemy liczbę
: w pierwszym kroku dopisujemy liczbę 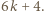 Wreszcie liczba podzielna przez
Wreszcie liczba podzielna przez 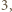 powiedzmy
powiedzmy 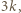 może zostać uzyskana w siedmiu krokach z liczby
może zostać uzyskana w siedmiu krokach z liczby 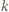 : w kolejnych pośrednich krokach dopisujemy
: w kolejnych pośrednich krokach dopisujemy 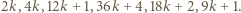
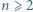 o następującej własności: Liczby całkowite od
o następującej własności: Liczby całkowite od 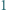 do
do 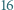 można tak wpisać w pola tablicy
można tak wpisać w pola tablicy 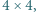 aby sumy liczb w wierszach i kolumnach były ośmioma parami różnymi liczbami całkowitymi, z których każda jest podzielna przez
aby sumy liczb w wierszach i kolumnach były ośmioma parami różnymi liczbami całkowitymi, z których każda jest podzielna przez 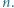
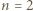 oraz
oraz 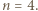
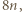 a z drugiej - nie większa od
a z drugiej - nie większa od 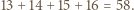 Stąd wniosek, że
Stąd wniosek, że 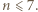 Ponadto suma ośmiu rozważanych sum jest równa dwukrotności sumy wszystkich liczb wpisanych w pola tablicy, czyli
Ponadto suma ośmiu rozważanych sum jest równa dwukrotności sumy wszystkich liczb wpisanych w pola tablicy, czyli 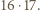 Liczba
Liczba 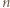 jest dzielnikiem tej sumy, wobec czego
jest dzielnikiem tej sumy, wobec czego 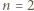 lub
lub 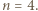 Poniższy przykład pozwala stwierdzić, że te wartości
Poniższy przykład pozwala stwierdzić, że te wartości  w istocie są osiągalne.
w istocie są osiągalne.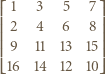
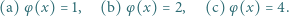
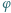 oznacza funkcję Eulera.
oznacza funkcję Eulera.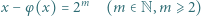
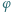 oznacza funkcję Eulera.
oznacza funkcję Eulera.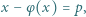
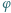 jest funkcją Eulera, a
jest funkcją Eulera, a 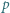 jest daną liczbą pierwszą. Wykazać, że równanie (*):
jest daną liczbą pierwszą. Wykazać, że równanie (*):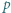 ).
).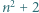 oraz
oraz 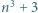 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 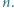
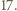
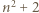 oraz
oraz 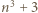 dzieli również liczbę
dzieli również liczbę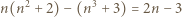
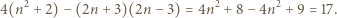
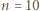 mamy
mamy 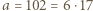 oraz
oraz 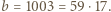
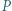 o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite
o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite 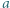 i
i 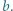 Udowodnić, że jeśli
Udowodnić, że jeśli 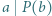 oraz
oraz 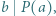 to
to 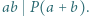
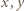 ma miejsce podzielność
ma miejsce podzielność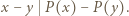
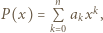 mamy
mamy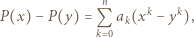
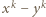 jest podzielna przez
jest podzielna przez 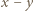 (w razie potrzeby przyjmujemy
(w razie potrzeby przyjmujemy 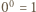 ).
).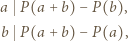
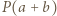 jest liczbą podzielną zarówno przez
jest liczbą podzielną zarówno przez 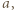 jak i przez
jak i przez 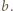 Pozostaje skorzystać z założenia, że liczby
Pozostaje skorzystać z założenia, że liczby 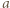 i
i 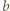 są względnie pierwsze.
są względnie pierwsze.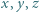 spełniające równanie
spełniające równanie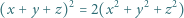
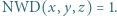
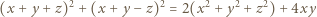

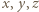 spełniają warunki zadania, to iloczyny
spełniają warunki zadania, to iloczyny 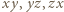 są nieujemne, co oznacza, że liczby
są nieujemne, co oznacza, że liczby 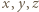 są wszystkie nieujemne lub wszystkie niedodatnie.
są wszystkie nieujemne lub wszystkie niedodatnie.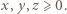 Ze związku (1) (oraz warunku, że
Ze związku (1) (oraz warunku, że 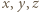 nie mają wspólnego dzielnika
nie mają wspólnego dzielnika 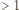 ) wynika, że
) wynika, że 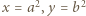 dla pewnej pary liczb całkowitych
dla pewnej pary liczb całkowitych 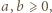 względnie pierwszych. Przepisujemy (1) jako
względnie pierwszych. Przepisujemy (1) jako 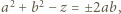 czyli
czyli 
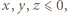 widzimy, że trójka
widzimy, że trójka 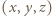 ma postać
ma postać
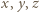 ma taką postać (więc
ma taką postać (więc 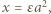
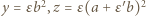 ;
; 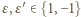 ), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby
), wówczas spełnione jest równanie (1) (równoważne wyjściowemu), zaś liczby 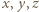 są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.
są względnie pierwsze. Wzór (2) przedstawia więc ogólne rozwiązanie postawionego zagadnienia.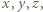 po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych
po ewentualnej jednoczesnej zmianie znaku, są kwadratami trzech względnie pierwszych liczb całkowitych, z których jedna jest sumą dwóch pozostałych zachodzi podzielność
zachodzi podzielność
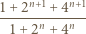
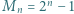 dla
dla 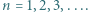 Udowodnić, że następujące dwa warunki są równoważne:
Udowodnić, że następujące dwa warunki są równoważne: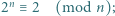
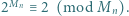
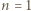 oba warunki są spełnione. Dalej przyjmujemy
oba warunki są spełnione. Dalej przyjmujemy 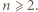 Zapiszmy liczbę
Zapiszmy liczbę 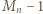 jako
jako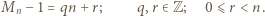
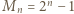 mamy kongruencję
mamy kongruencję 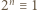 (mod
(mod 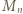 ), którą podnosimy do potęgi
), którą podnosimy do potęgi 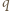 :
: 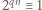 (mod
(mod 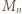 ); stąd po pomnożeniu przez
); stąd po pomnożeniu przez 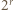 (i uwzględnieniu (1)):
(i uwzględnieniu (1)):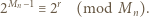
 jest dzielnikiem liczby
jest dzielnikiem liczby 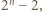 równej
równej 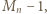 czyli w równości (1) jest
czyli w równości (1) jest 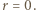 Ze związku (2) dostajemy
Ze związku (2) dostajemy 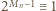 (mod
(mod 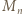 ); pomnożenie przez 2 daje warunek (ii).
); pomnożenie przez 2 daje warunek (ii).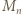 ) dzielimy stronami przez 2 (to dozwolone, bo
) dzielimy stronami przez 2 (to dozwolone, bo 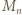 jest liczbą nieparzystą), otrzymując
jest liczbą nieparzystą), otrzymując 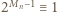 (mod
(mod 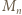 ). W połączeniu z (2) dostajemy
). W połączeniu z (2) dostajemy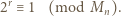
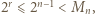 więc kongruencja (3) jest równością, skąd
więc kongruencja (3) jest równością, skąd 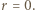 To znaczy, w myśl (1), że
To znaczy, w myśl (1), że  dzieli liczbę
dzieli liczbę 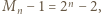 i mamy warunek (i).
i mamy warunek (i).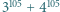 jest podzielna przez 13, 49, 181, 379, a nie jest podzielna przez 5 ani 11.
jest podzielna przez 13, 49, 181, 379, a nie jest podzielna przez 5 ani 11.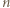 jest nieparzyste,
jest nieparzyste, 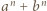 dzieli się przez
dzieli się przez 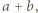 i wystarczy zauważyć, że
i wystarczy zauważyć, że 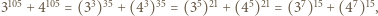 a więc
a więc 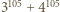 dzieli się przez
dzieli się przez 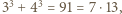 przez
przez 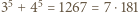 oraz przez
oraz przez 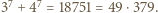
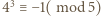 i
i 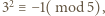 podobnie
podobnie 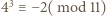 i
i 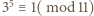 ).
).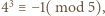 to
to 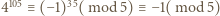 ; podobnie z
; podobnie z 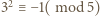 wynika
wynika 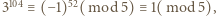 a więc
a więc 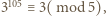 skąd
skąd 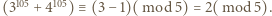
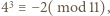 więc
więc 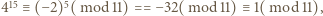 stąd
stąd 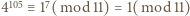 ; podobnie z
; podobnie z 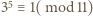 mamy
mamy 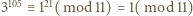 ; wobec tego
; wobec tego 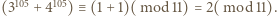
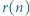 sumę
sumę  liczb będących resztami z dzielenia dodatniej liczby całkowitej
liczb będących resztami z dzielenia dodatniej liczby całkowitej 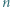 przez
przez 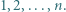 Udowodnij, że istnieje nieskończenie wiele takich
Udowodnij, że istnieje nieskończenie wiele takich 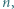 że
że 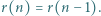
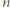 przez liczbę
przez liczbę 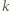 jest równa
jest równa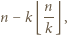
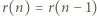 można przepisać jako
można przepisać jako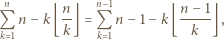
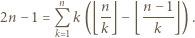
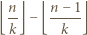
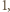 jeżeli
jeżeli 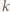 dzieli
dzieli  oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako
oraz 0 w przeciwnym przypadku. Stąd wniosek, że powyższy warunek można przepisać jako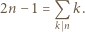
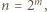 gdzie
gdzie 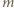 jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb
jest dodatnią liczbą całkowitą. Przykładową nieskończoną rodzinę liczb  spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.
spełniających warunek zadania stanowią więc wszystkie potęgi dwójki.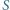 oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.
oraz nieskończenie wiele dodatnich liczb całkowitych, które można zapisać w takiej postaci.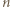 jest liczbą podzielną przez
jest liczbą podzielną przez 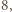 to
to  nie można zapisać w postaci sumy dwóch elementów zbioru
nie można zapisać w postaci sumy dwóch elementów zbioru 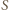 albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru
albo - w myśl tezy poprzedniego zadania - w postaci iloczynu dwóch elementów zbioru 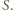 Przypuśćmy, że
Przypuśćmy, że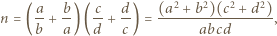
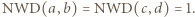 Skoro
Skoro 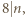 to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez
to co najmniej jeden z czynników w liczniku powyższego ułamka jest podzielny przez 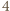 ; bez straty ogólności załóżmy, że
; bez straty ogólności załóżmy, że 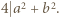 Stąd wynika, że liczby
Stąd wynika, że liczby 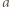 i
i 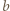 są tej samej parzystości, skąd wobec
są tej samej parzystości, skąd wobec 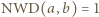 - obie są nieparzyste. Jednak wówczas
- obie są nieparzyste. Jednak wówczas 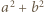 daje resztę
daje resztę 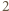 przy dzieleniu przez
przy dzieleniu przez 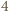 - sprzeczność.
- sprzeczność.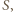 rozważymy ciąg Fibonacciego
rozważymy ciąg Fibonacciego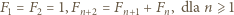
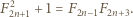
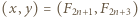 mamy więc
mamy więc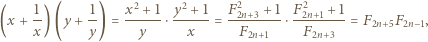
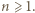 To kończy dowód, gdyż dla różnych
To kończy dowód, gdyż dla różnych 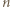 otrzymujemy różne liczby.
otrzymujemy różne liczby.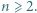
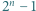 jest bezkwadratowa, to liczby
jest bezkwadratowa, to liczby 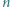 oraz
oraz 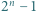 są względnie pierwsze.
są względnie pierwsze. oraz
oraz 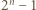 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 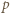 (jasne, że
(jasne, że 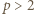 ). Wykażemy, że wówczas liczba
). Wykażemy, że wówczas liczba 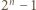 dzieli się przez
dzieli się przez 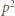 (nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata,
(nie jest więc bezkwadratowa). Zgodnie z małym twierdzeniem Fermata, 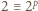 (mod
(mod 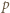 ). Podnosimy tę kongruencję stronami do potęgi
). Podnosimy tę kongruencję stronami do potęgi 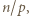 otrzymując
otrzymując 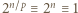 (mod
(mod 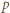 ). Zatem
). Zatem 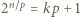 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 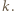 Stąd
Stąd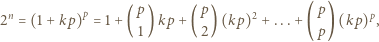
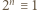 (mod
(mod 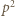 ); a to była nasza teza.
); a to była nasza teza.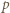 kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie
kontroluje dwie końcowe cyfry rozwinięcia (przy podstawie 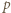 ) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki
) kolejnych potęg dwójki, pozwala znaleźć moment powtórzenia końcówki 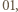 czyli wykładnik
czyli wykładnik 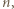 dla którego
dla którego 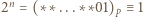 (mod
(mod 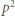 ). Powtarzamy tę procedurę dla kolejnych liczb pierwszych
). Powtarzamy tę procedurę dla kolejnych liczb pierwszych 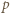 ; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do
; warto przy tym, dla oszczędności czasu, ograniczyć zakres wykładnika, np. do 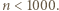 W ten sposób szybko znajdujemy parę
W ten sposób szybko znajdujemy parę 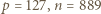 ; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki
; nie jest ona jednak szukanym kontrprzykładem, bowiem dla tej pary zachodzą związki 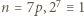 (mod
(mod 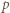 ), z których nietrudno wynika, że liczby
), z których nietrudno wynika, że liczby  i
i 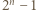 nie są względnie pierwsze.
nie są względnie pierwsze.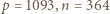 jest już dobra: gdyby liczby
jest już dobra: gdyby liczby 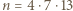 oraz
oraz  nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki
nie były względnie pierwsze, ta ostatnia musiałaby się dzielić przez 7 lub 13; ale minimalne wykładniki 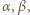 dla których
dla których 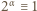 (mod 7),
(mod 7), 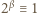 (mod 13), to
(mod 13), to 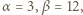 więc wykładnik
więc wykładnik 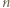 musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność
musiałby się dzielić przez 3; a tak nie jest. Skoro zaś ta para została wygenerowana przez algorytm, zapewniający podzielność 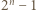 przez
przez 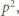 zatem liczba
zatem liczba 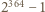 nie jest bezkwadratowa.
nie jest bezkwadratowa.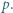 Funkcja
Funkcja 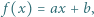 gdzie
gdzie 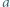 i
i 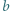 są liczbami całkowitymi, ma tę własność, że liczby
są liczbami całkowitymi, ma tę własność, że liczby
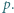 Wykazać, że
Wykazać, że 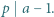
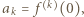 gdzie
gdzie 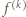 oznacza
oznacza 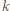 -krotne złożenie funkcji
-krotne złożenie funkcji 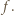 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 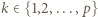 mamy
mamy 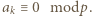 Jeżeli
Jeżeli 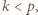 to
to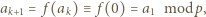
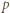 wyrazów ciągu
wyrazów ciągu 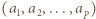 są parami różne. To oznacza, że
są parami różne. To oznacza, że 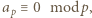 czyli
czyli 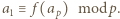
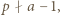 czyli
czyli 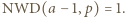 Wówczas istnieją takie liczby całkowite
Wówczas istnieją takie liczby całkowite 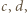 że
że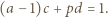
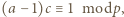 czyli
czyli 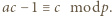 Z warunków zadania wynika, że dla pewnego
Z warunków zadania wynika, że dla pewnego 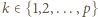 mamy
mamy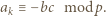
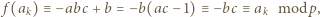
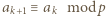 (gdzie w razie potrzeby przyjmujemy
(gdzie w razie potrzeby przyjmujemy 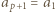 ). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez
). To stoi w sprzeczności z założeniem, że reszty z dzielenia przez 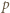 wyrazów ciągu
wyrazów ciągu 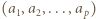 są parami różne.
są parami różne.