Klub 44M - zadania XII 2020»Zadanie 812
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2020
- Publikacja w Delcie: grudzień 2020
- Publikacja elektroniczna: 1 grudnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (421 KB)
-
Zadanie 812 zaproponował pan Tomasz Ordowski.
Udowodnić, że dla każdej liczby naturalnej 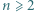 iloczyn
iloczyn 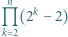 dzieli się przez
dzieli się przez 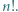
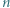
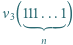
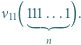
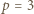 wystarczy rozważyć
wystarczy rozważyć 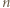 podzielne przez 3, a dla
podzielne przez 3, a dla 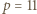 - rozważyć
- rozważyć  parzyste. Dla
parzyste. Dla 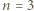 skorzystać z równości
skorzystać z równości 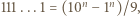 a dla
a dla 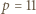 i
i 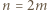 z równości
z równości 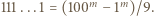
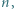
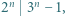
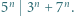
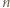 zachodzi nierówność
zachodzi nierówność 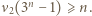 Wartość
Wartość 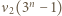 można wyznaczyć dokładnie, w zależności od parzystości
można wyznaczyć dokładnie, w zależności od parzystości 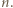 Skorzystać z nierówności
Skorzystać z nierówności 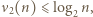 aby wykazać, że
aby wykazać, że 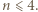
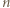 parzystych
parzystych 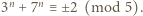 Dla
Dla 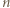 nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).
nieparzystych skorzystać z lematu w wersji z dodawaniem i postępować podobnie jak w podpunkcie (a).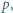
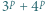
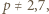 to
to 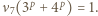
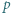 -adycznego w
-adycznego w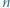
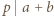 i
i 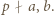 W przypadku
W przypadku 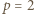 mamy
mamy 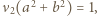 natomiast dla
natomiast dla 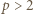 mamy
mamy 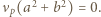
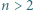
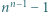
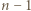 i stwierdzić, że
i stwierdzić, że 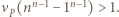

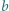
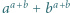
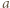 i
i 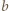 mają wspólny dzielnik pierwszy
mają wspólny dzielnik pierwszy 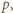 to
to 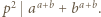 W przeciwnym razie istnieje liczba pierwsza
W przeciwnym razie istnieje liczba pierwsza 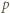 spełniająca warunki
spełniająca warunki 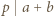 i
i 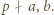 Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.
Wystarczy skorzystać z lematu w wersji z dodawaniem, rozumując podobnie jak w poprzednim zadaniu.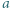
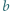
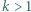
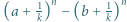
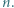
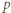 będzie dowolnym dzielnikiem pierwszym liczby
będzie dowolnym dzielnikiem pierwszym liczby 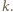 Jeśli liczba z zadania jest całkowita, to
Jeśli liczba z zadania jest całkowita, to 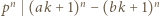 i można skorzystać z lematu, bo
i można skorzystać z lematu, bo 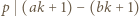 oraz
oraz 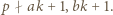
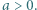
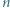
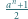
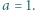
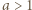 liczba
liczba 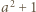 ma dzielnik pierwszy
ma dzielnik pierwszy 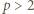 i dla odpowiednio dobranego nieparzystego
i dla odpowiednio dobranego nieparzystego 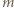 liczba
liczba 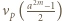 nie dzieli się przez 3.
nie dzieli się przez 3.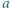
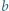
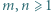
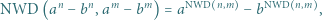
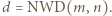 Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych
Stosując własności kongruencji, uzasadnić, że zbiór tych całkowitych 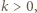 dla których
dla których 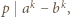 jest postaci
jest postaci 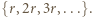
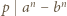 i
i 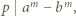 to
to 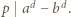
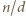 i
i 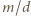
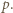 Wywnioskować z tego, że
Wywnioskować z tego, że 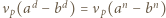 lub
lub 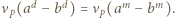
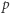 -adyczne
-adyczne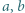
 :
:
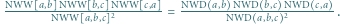
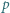
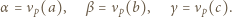
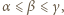
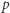 -adyczne
-adyczne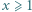
![|[x, 2x]](/math/temat/matematyka/teoria_liczb/zadania/2020/11/01/zm-20-11-kpo-2/2x-d7608384ddd380a3dd1f65eb0be5d8496d7a9363-im-2C,6B,73-FF,FF,FF.gif)
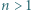 :
: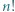
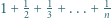
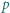
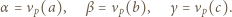
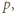
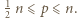
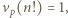
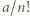
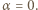
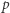 -adyczne
-adyczne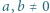
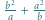
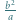
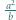
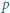
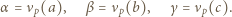
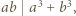
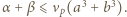
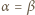
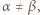
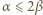
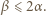
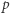 -adyczne
-adyczne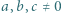
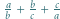
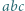
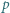
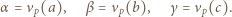
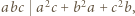
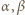
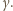
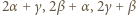
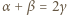
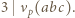
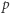 -adyczne
-adyczne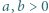
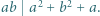

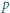
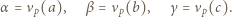
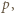
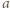
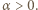

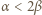
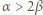
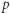 -adyczne
-adyczne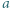
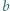
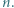
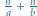
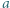
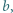
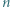
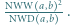
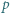
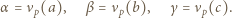
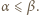
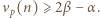
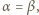
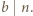
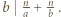
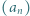 jest określony wzorami
jest określony wzorami 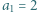 ;
; 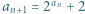 dla
dla 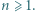 Niech
Niech 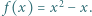 Udowodnić, że dla każdego
Udowodnić, że dla każdego 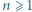 liczba
liczba 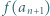 dzieli się przez
dzieli się przez 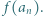
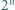 jedynek ma co najmniej
jedynek ma co najmniej 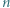 różnych dzielników pierwszych.
różnych dzielników pierwszych.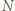 będzie liczbą składającą się w zapisie dziesiętnym z
będzie liczbą składającą się w zapisie dziesiętnym z 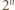 jedynek. Mamy
jedynek. Mamy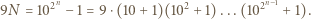
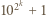 i
i 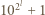 są względnie pierwsze dla
są względnie pierwsze dla 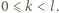 Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą
Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą 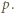 Oczywiście liczba
Oczywiście liczba 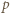 jest nieparzysta. Ponieważ
jest nieparzysta. Ponieważ 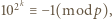 więc
więc 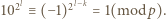 Skoro jednak
Skoro jednak 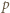 dzieli
dzieli 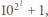 to
to 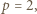 co przeczy wcześniej poczynionej uwadze o nieparzystości
co przeczy wcześniej poczynionej uwadze o nieparzystości 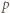 i kończy rozwiązanie zadania.
i kończy rozwiązanie zadania.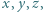 że
że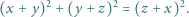
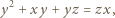
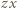 do obu stron daje
do obu stron daje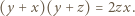
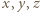 są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.
są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.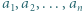 spełniają równości
spełniają równości 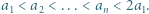 Udowodnić, że jeśli
Udowodnić, że jeśli 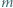 jest liczbą różnych dzielników pierwszych iloczynu
jest liczbą różnych dzielników pierwszych iloczynu 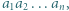 to
to 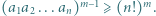
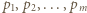 będą różnymi dzielnikami pierwszymi iloczynu
będą różnymi dzielnikami pierwszymi iloczynu 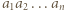 oraz niech
oraz niech 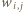 oznacza wykładnik liczby
oznacza wykładnik liczby 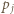 w rozkładzie
w rozkładzie 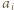 na czynniki pierwsze dla
na czynniki pierwsze dla 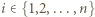 i
i 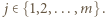 W pole tabeli o współrzędnych
W pole tabeli o współrzędnych 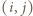 wpisujemy
wpisujemy 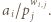 Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej
Należy zaobserwować, że w każdym wierszu są różne liczby całkowite dodatnie, więc ich iloczyn wynosi co najmniej 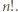 Ponadto iloczyny liczb w kolejnych kolumnach są równe
Ponadto iloczyny liczb w kolejnych kolumnach są równe