Zadanie ZM-1215
o zadaniu...
- Publikacja w Delcie: sierpień 2008
- Publikacja elektroniczna: 02-02-2011
Dane są liczby całkowite dodatnie
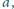
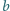 o następującej własności:
o następującej własności:
dla każdej liczby całkowitej dodatniej
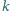 liczby
liczby
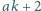 oraz
oraz
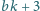 nie są względnie pierwsze. Udowodnić, że
nie są względnie pierwsze. Udowodnić, że
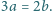
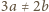 i przyjmijmy
i przyjmijmy
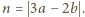 Wtedy
Wtedy
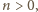 a więc liczby
a więc liczby
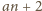 oraz
oraz
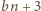 mają
wspólny dzielnik
mają
wspólny dzielnik
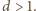 Zatem liczba
Zatem liczba
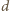 jest także dzielnikiem
liczby
jest także dzielnikiem
liczby
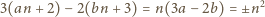
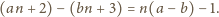
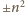 i
i
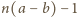 są względnie pierwsze: każdy dzielnik pierwszy
są względnie pierwsze: każdy dzielnik pierwszy
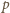 liczby
liczby
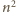 jest
także dzielnikiem liczby
jest
także dzielnikiem liczby
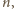 a więc
a więc
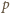 nie może być dzielnikiem
liczby
nie może być dzielnikiem
liczby
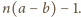 Wobec tego
Wobec tego
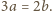
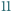 o tej własności, że każda inna 19-cyfrowa liczba otrzymana z N poprzez zmianę kolejności (permutację) jej cyfr nie jest podzielna przez
o tej własności, że każda inna 19-cyfrowa liczba otrzymana z N poprzez zmianę kolejności (permutację) jej cyfr nie jest podzielna przez 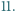
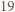 -cyfrowa liczba
-cyfrowa liczba 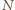 istnieje, np.
istnieje, np. 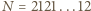
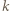 -cyfrowa liczba
-cyfrowa liczba 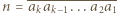 jest podzielna przez
jest podzielna przez 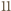 wtedy i tylko wtedy, gdy liczba
wtedy i tylko wtedy, gdy liczba 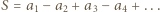 jest podzielna przez
jest podzielna przez 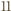 . Stąd wynika, że liczba
. Stąd wynika, że liczba 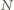 jest podzielna przez
jest podzielna przez 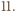
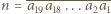 otrzymana z
otrzymana z 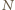 poprzez permutaję jej cyfr nie jest podzielna przez
poprzez permutaję jej cyfr nie jest podzielna przez 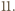
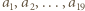 liczby
liczby 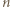 jest dokładnie
jest dokładnie 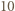 dwójek i
dwójek i 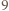 jedynek, więc liczba
jedynek, więc liczba 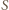 jest nieparzysta. Ponadto
jest nieparzysta. Ponadto 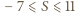 . Stąd wynika, że liczba
. Stąd wynika, że liczba 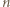 jest podzielna przez
jest podzielna przez 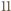 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 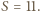 To jednak jest możliwe jedynie wtedy, gdy
To jednak jest możliwe jedynie wtedy, gdy 