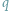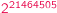Delta mi!

Jak wiele innych ważnych twierdzeń matematyki, zasadnicze twierdzenie algebry, udowodnione przez Carla Friedricha Gaussa w ostatnim roku osiemnastego stulecia, informuje nas, że pewne obiekty nie istnieją. Mianowicie, nie ma takiego, różnego od stałej, wielomianu zmiennej zespolonej, który nie znikałby w żadnym punkcie płaszczyzny zespolonej

Jeśli liczba naturalna jest największą liczbą pierwszą, to...

Nie wiem, czy wielu Czytelników Delty słyszało o szczęśliwych liczbach. Nie chodzi tu o to, że często siódemkę uważa się za liczbę szczęśliwą, trzynastkę zaś za pechową, ale o matematyczne pojęcie.

W matematyce, z jaką spotykamy się w szkole i na uniwersytecie, linię prostą identyfikuje się ze zbiorem punktów, w którym współrzędnymi są liczby rzeczywiste. Istnieje jednakże argument przeciw takiemu konkretnemu utożsamieniu, który opiera się na tym, iż nieskończenie wiele własności linii prostej nie może być ani dowiedzionych, ani obalonych za pomocą aksjomatów używanych w teorii mnogości (tzw. aksjomatów Zermelo–Fraenkla).

Na ogół matematycy nie są ulubionymi gośćmi na przyjęciach. Poprzedza nas reputacja nudziarzy, zanurzonych myślami w definicjach i twierdzeniach. A jednak możemy użyć naszej wiedzy, by oczarować zebranych magicznymi trikami, opartymi na własnościach matematycznych. Może przy okazji ktoś zainteresuje się matematyką?

Ludzie od niepamiętnych czasów prześcigali się w biciu rekordów w najprzeróżniejszych dziedzinach, od czysto sportowych (szybciej, wyżej, mocniej), poprzez cywilizacyjne (wyższe budowle, większe samoloty, szybsze komputery), aż po całkiem absurdalne, żeby nie powiedzieć głupie.

Oto spektakularne wyniki z lat 1997–2009, dotyczące liczb pierwszych.

O potęgach dwójki i własnościach ich rozwinięć dziesiętnych można było w Delcie poczytać wielokrotnie, m.in. w artykułach Zbigniewa Marciniaka i wyżej podpisanego. Istnieją zapewne osoby, które nie czytały tych artykułów, dlatego że kilkanaście lat temu nie umiały jeszcze czytać, choć dziś Deltę czytują. Być może jest to dostatecznym usprawiedliwieniem, żeby napisać o całej sprawie jeszcze raz.

Geometryczną interpretacją ciała liczb zespolonych jest płaszczyzna. Za pomocą liczb zespolonych można opisywać własności figur i przekształceń na płaszczyźnie. Oto kilka przykładów takich zastosowań...