Niewymierność
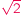 i jeszcze większe niemożliwości
i jeszcze większe niemożliwości
Punktem wyjścia niech będzie najsłynniejsza chyba matematyczna konstatacja, ta
mianowicie, że liczba
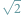 jest niewymierna...
jest niewymierna...
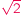 i jeszcze większe niemożliwości
i jeszcze większe niemożliwościPunktem wyjścia niech będzie najsłynniejsza chyba matematyczna konstatacja, ta
mianowicie, że liczba
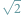 jest niewymierna...
jest niewymierna...
3, 7, 31, 211, 2311, ... – jaki jest następny wyraz tego ciągu? Jakiś czas temu taka zagadka pojawiła się na jednej z polskich rozrywkowych stron internetowych. Niemal od razu w komentarzach pod nią rozpoczął się spór o poprawne, prawdziwe rozwiązanie. Czytelnik zapewne zechce podjąć wyzwanie samodzielnego odnalezienia następnego elementu ciągu i jego ogólnej reguły. Zatem zatrzymajmy się tu i pozwólmy sobie na chwilę namysłu; w dalszej części tekstu pojawi się rozwiązanie (autorowi niniejszego tekstu zajęło kilka dłuższych chwil znalezienie formuły).
Matematyka, jak przystało na królową nauk, jest dyscypliną dość trudną i wymagającą umiejętności abstrakcyjnego myślenia. Jeżeli przyjąć za Galileuszem, że matematyka jest alfabetem, za pomocą którego Bóg opisał wszechświat, to trzeba przyznać, że jest to alfabet dość złożony i nie jest łatwo nauczyć się dobrze nim posługiwać. Jednym z jego ważniejszych elementów jest niewątpliwie nieskończoność.
Za pomocą kolorowania wielomianów można udowodnić Zasadnicze twierdzenie algebry w zaskakująco elementarny sposób...
Rozwiązywanie równań diofantycznych jest jednym z ważniejszych problemów
klasycznej teorii liczb. Czytelnicy tego artykułu na pewno słyszeli o równaniu Pella
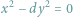 czy równaniu Fermata
czy równaniu Fermata
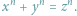
W dowodzeniu nierówności często pomocna bywa tak zwana metoda stycznych. Zdarza się, że wykres funkcji leży nad pewną prostą styczną do niego lub pod taką prostą (wszędzie lub tylko na jakimś przedziale). To oznacza, że możemy oszacować wartości tej funkcji przez wartości funkcji liniowej, której wykresem jest wybrana styczna. Żeby takie oszacowanie doprowadziło do celu, wybrana styczna musi przechodzić przez punkt, dla którego badana nierówność jest równością. Przyjrzymy się kilku przykładom zastosowań tej metody.
Niejeden maturzysta marzy zapewne, żeby na egzaminie dojrzałości rozwiązywać
następujące, z pozoru błahe, zadanie: Wyznacz liczbę miejsc zerowych funkcji
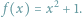 Abiturienta nie zraziłaby prawdopodobnie nawet drobna
przeszkoda, jaką jest wyraźny brak informacji o dziedzinie funkcji
Abiturienta nie zraziłaby prawdopodobnie nawet drobna
przeszkoda, jaką jest wyraźny brak informacji o dziedzinie funkcji
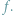 Z uwagi
na wszechobecność zbioru liczb rzeczywistych w obecnym programie nauczania
wydaje się, że o żadnych zerach mowy być nie może. Nawet słynna „delta” nie jest
tu potrzebna.
Z uwagi
na wszechobecność zbioru liczb rzeczywistych w obecnym programie nauczania
wydaje się, że o żadnych zerach mowy być nie może. Nawet słynna „delta” nie jest
tu potrzebna.
Chyba wszyscy lubimy liczby pierwsze. Szczególne wrażenie robią te naprawdę duże, wydają się skrywać w sobie jakąś nadzwyczajną tajemnicę: dlaczego akurat one stały się swego rodzaju wybrańcami spośród innych liczb i mają tak niezwykłe właściwości?
Sprawdź, Czytelniku, czy potrafisz...
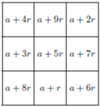
Zamieszczony w poprzednim numerze, jako zapowiedź tego numeru, widoczny obok
kwadrat magiczny jest dla
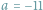 (lub
(lub
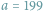 ) i
) i
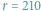 złożony
z samych liczb pierwszych.
złożony
z samych liczb pierwszych.
Gry, zagadki, paradoksy Drobiazgi
W Delcie 3/1979 zamieściliśmy największy znany wówczas kwadrat magiczny złożony z różnych liczb pierwszych – było ich 169. Co więcej, był to kwadrat „cebulkowy”. A dziś – proszę: istnieje już „cebulkowy” kwadrat magiczny aż o trzy większy, złożony zatem z dwustu pięćdziesięciu sześciu liczb pierwszych. I jak tu nie wierzyć w postęp!
Sophie Germain (1776–1831), wbrew ówczesnym obyczajom matematyk, fizyk, metalurg i autorka ciekawych szkiców o kulturze, prawie na każdym kroku musiała udowadniać swą wiedzę i bronić swych dokonań przed rzeszami niedowiarków.
Twierdzenie o jednoznaczności rozkładu na czynniki pierwsze w zbiorze liczb
naturalnych wypowiada się najprościej w następujący sposób: każdą liczbę naturalną
różną od jedności możemy przedstawić w postaci iloczynu
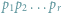 liczb
pierwszych na jeden tylko sposób, o ile rozkłady, różniące się kolejnością
czynników, uważać będziemy za równe...
liczb
pierwszych na jeden tylko sposób, o ile rozkłady, różniące się kolejnością
czynników, uważać będziemy za równe...
Co to jest liczba pierwsza? Najkrótsza definicja mówi, że to taka liczba naturalna, która ma dokładnie dwa dzielniki. Każda liczba naturalna ma przynajmniej dwa dzielniki: 1 i samą siebie. Wyjątkiem jest jedynka, dla której te dwa dzielniki okazują się tym samym.
Załóżmy, że suma kw adratów trzech liczb naturalnych jest podwojonym kwadratem pewnej liczby naturalnej. Czy możliwe jest, żeby wówczas suma czwartych potęg tych trzech liczb była podwojoną czwartą potęgą tej samej liczby?
Każdy od czasu do czasu potrzebuje metody przekazania komuś pewnych wiadomości tak, żeby niepowołane osoby nie miały szans na ich przechwycenie. Począwszy od zabaw z kolegami na podwórku, a skończywszy na operacjach bankowych, wojskowych czy wykorzystujących dane osobowe – bez szyfrów po prostu nie da się żyć. Do zaszyfrowania danych zwykle potrzebny jest klucz – pewne słowo czy liczba, które najpierw kierują procesem tworzenia szyfru, a później pozwalają odbiorcy wiadomości ją odkodować. Osoby, które chcą porozumiewać się za pomocą szyfru, muszą najpierw uzgodnić klucz między sobą. I tu pojawia się problem: jak ustalić klucz, tak żeby nikt oprócz nas nie mógł go poznać?

Gdy poznajemy matematykę, liczby oznaczane symbolami
 oraz
oraz
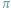 pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
 jest liczbą niewymierną (L. Euler, 1737 r.) oraz
jest liczbą niewymierną (L. Euler, 1737 r.) oraz
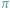 jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
 wykazał
Ch. Hermite w 1873 r., a przestępność liczby
wykazał
Ch. Hermite w 1873 r., a przestępność liczby
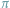 wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.
wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.
Trzy kółeczka łatwo ułożyć w trójkąt foremny (czyli równoboczny), cztery w czworokąt foremny (czyli kwadrat), pięć w pięciokąt foremny itd. Można więc 3 uważać za liczbę trójkątną, cztery za czworokątną, pięć za pięciokątną itd. Rysunki poniżej pokazują, jak można, rysując kropki, określić inne liczby wielokątne.