Teoria liczb Kącik początkującego olimpijczyka
Lemat o zwiększaniu wykładnika p-adycznego
O zależnościach między 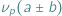 i
i 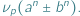
Teoria liczb Kącik początkującego olimpijczyka
O zależnościach między 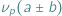 i
i 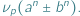
Teoria liczb Kącik początkującego olimpijczyka
 -adyczne
-adyczneO wygodnym narzędziu, przydatnym wszędzie tam, gdzie spotykamy rozkład na czynniki pierwsze

John William Strutt
Lord Rayleigh, właściwie John William Strutt, 3. Baron Rayleigh (1842-1919) był laureatem Nagrody Nobla w dziedzinie fizyki w 1904 r. (badanie gęstości gazów i odkrycie, wspólnie z Sir W. Ramsayem, argonu). W 1877 roku w książce The Theory of Sound (vol. I, str. 123) opisał prawidłowość, którą można wyrazić następująco...
Wielomian jaki jest, każdy widzi. I każdy, kto widzi, wie również, że wielomiany miewają pierwiastki rzeczywiste (czyli miejsca zerowe), ale nie zawsze...

Andreas Scheits
Gottfried Wilhelm Leibniz
W marcu 1672 roku do Paryża przybył z misją dyplomatyczną od elektora mogunckiego młody prawnik, filozof i erudyta Gottfried Wilhelm Leibniz (1646-1716). Spotkanie z Christiaanem Huygensem (jesienią 1672 r.) przekonało Leibniza, że w matematyce jest nowicjuszem. Huygens, chcąc zbadać matematyczną przenikliwość Leibniza, rzucił mu takie oto wyzwanie: wyznaczyć sumę szeregu 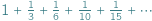 Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...
Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...
Piramidy w starożytnym Egipcie budowano na kształt ostrosłupa prawidłowego o podstawie kwadratu. Jak pokazują źródła historyczne, starożytni Egipcjanie potrafili obliczyć objętość takiego ostrosłupa. Jednak ich dobrze rozwinięta, jak na tamte czasy, matematyka, miała głównie zastosowanie praktyczne i raczej nikt nie formułował pytań, które miałyby na celu jedynie matematyczną rozrywkę. Jednym z matematyków, który szczególnie interesował się rozrywkowymi zastosowaniami królowej nauk, był Édouard Lucas, autor między innymi słynnej gry zwanej Wieżą Hanoi. W niniejszym artykule zwrócimy uwagę na sformułowany przez Lucasa problem z gatunku tych raczej mało praktycznych. Jak zobaczymy, ma on pewien związek z piramidami.
Algebra Kącik początkującego olimpijczyka
Standardowym postępowaniem jest ujednorodnianie dowodzonych nierówności za pomocą danego w zadaniu warunku. Ciekawiej jest na odwrót - gdy mamy udowodnić jednorodną nierówność, możemy często założyć coś dodatkowo o występującej w niej zmiennych. Naprawdę!

Leonardo Fibonacci (1170-1240)
Fibonacci (właściwie Leonardo z Pizy, ok. 1170-1240) nauczył się zasad arytmetyki hindusko-arabskiej, gdy razem z ojcem przebywał w Bougie (obecnie algierska Bidżaja). Poszerzał swoją wiedzę podczas podróży do Egiptu, Syrii, Grecji, na Sycylię, do Prowansji. Gdy osiadł w Pizie, w 1202 roku napisał traktat Liber Abaci (Księga rachunków), z myślą o rozpowszechnieniu w Europie notacji dziesiętnej opartej na wykorzystaniu cyfr 0,1,2, ...,9. Pokazał w nim użyteczność nowych metod na wielu przykładach rachunkowych, szczególnie związanych z przeliczaniem miar i wag, obliczaniem zysków i odsetek, wymianą pieniędzy...
Człowiek twardo stąpa po ziemi, a z nim pojęcia, które stworzył. Na przykład liczby są tylko tym, do czego człowiekowi służą: porządkowe, kardynalne i inne. W skończonych zastosowaniach są to liczby naturalne 1, 2, 3, ... i ich uogólnienia: liczby całkowite, wymierne, rzeczywiste i zespolone. Słowo skończone w poprzednim zdaniu odnosi się wyłącznie do opisywanego atrybutu liczonego obiektu: a to jego rangi, a to mocy, a to fizycznych rozmiarów. W matematyce teoretycznej liczb praktycznie zawsze potrzebujemy nieskończenie wiele!
Każda funkcja ciągła określona na zbiorze liczb rzeczywistych ma własność Darboux, tzn. jeśli dla pewnych 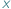 i
i 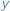 mamy
mamy 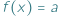 i
i 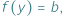 to w przedziale
to w przedziale 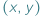 są przyjmowane wszystkie wartości między
są przyjmowane wszystkie wartości między  i
i 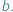 Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...
Jest to bardzo skuteczne narzędzie do rozwiązywania wielu zadań z analizy matematycznej. Okazuje się, że podobny motyw możemy zaobserwować także w zadaniach dotyczących liczb całkowitych...
Teoria liczb Kącik początkującego olimpijczyka
O pożytkach płynących z posługiwania się dziesiętnym systemem pozycyjnym.
Zapewne każdy Czytelnik Delty wie, jak sprawdzić, czy nawet duża liczba jest podzielna przez 3, czy przez 8. Metody tego typu wprowadzane są już w młodszych klasach szkoły podstawowej, dzięki czemu są powszechnie znane. Jednak tytułowy problem podzielności akurat przez 7 jest w typowym kursie szkolnym pomijany. W niniejszym artykule postanowiliśmy więc tę lukę uzupełnić i przedstawić przegląd różnych metod na sprawdzenie podzielności przez 7.
Być może nie wypada zadawać tytułowego pytania w numerze marcowym, gdyż w tym miesiącu obchodzone jest wspaniałe święto tej największej bodaj celebrytki pośród liczb rzeczywistych, jednak Delta nie pozwoli zakneblować sobie ust poprawnością polityczną. Tym bardziej, że w Internecie roi się od plotek i pogłosek na ten temat. Zamieszanie rozpoczęło się od utworzonego w dobrej wierze memu (zamieszczony poniżej), którego autor w poetycki sposób opisywał rzekomą, mistyczną własność 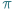 - jej rozwinięcie dziesiętne miałoby skrywać wszelkie tajemnice tego świata i odpowiedzi na wszystkie fundamentalne dla ludzkości pytania.
- jej rozwinięcie dziesiętne miałoby skrywać wszelkie tajemnice tego świata i odpowiedzi na wszystkie fundamentalne dla ludzkości pytania.
Zacznijmy od przypomnienia zadania 766 z Klubu 44M (Delta 9/2018)...
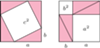
Są twierdzenia łatwe i trudne do udowodnienia. Zazwyczaj im mocniejsze sformułowanie, obejmujące więcej przypadków, tym trudniej się je dowodzi. Tak jest na przykład z twierdzeniem cosinusów i twierdzeniem Pitagorasa, które jest jego szczególnym przypadkiem. Łatwiej jest udowodnić twierdzenie Pitagorasa; można to zrobić nawet w sposób zrozumiały dla przedszkolaka (zobacz rysunek obok). Do dowodu twierdzenia cosinusów trzeba przynajmniej wiedzieć, co to cosinus, w szczególności kąta rozwartego.
Na początek krótka zagadka: co jest większe, 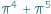 czy
czy 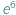 ? Drogi Czytelniku! Nie wysilaj się. Nie masz szans raczej tego poprawnie ocenić...
? Drogi Czytelniku! Nie wysilaj się. Nie masz szans raczej tego poprawnie ocenić...
Dawno temu... w czasach bez Internetu, bez gier komputerowych i smartfonów dzieci bawiły się w chowanego. Na początku zabawy trzeba było oczywiście wyznaczyć osobę, która będzie szukać. Uczestnicy ustawiali się w koło i ktoś odliczał: Raz, dwa, trzy, wychodź ty, i wówczas szósta osoba (odliczanka ma 6 sylab) wychodziła z kółka. Procedurę tę powtarzano aż do momentu, gdy w kółku pozostała jedna osoba - to był pierwszy szukający. Istnieje wiele wierszyków-odliczanek. Moją ulubioną jest odliczanka 15-sylabowa: Mama daje jeść, tata daje pić, a ty sobie idź.
Już rok po śmierci Gaussa (w 1856 r.) ukazała się książka wspomnieniowa jego wieloletniego przyjaciela Wolfganga Sartoriusa von Waltershausena Zum Gauss Gedächtniss. Trzeba o niej wiedzieć co najmniej z dwóch powodów. Stąd pochodzi najsłynniejszy aforyzm z matematyką w roli głównej. Jako teoretyk liczb przytoczę go z przyjemnością w pełnej postaci: Matematyka jest królową nauk, a arytmetyka królową matematyki.
Czytelnicy Delty zapewne znają zawody matematyczne dla uczniów, takie jak Olimpiada Matematyczna lub Kangur Matematyczny. Nie wszyscy wiedzą jednak, że konkursowe zmagania można kontynuować również podczas studiów. Na niektórych uczelniach odbywają się nawet specjalne zajęcia, podczas których rozwiązuje się i omawia zadania konkursowe.