Teoria liczb Konkurs prac uczniowskich
Uogólnione ciągi Fibonacciego
Skrót pracy nagrodzonej złotym medalem w konkursie Polskiego Towarzystwa Matematycznego i redakcji Delty na najlepszą pracę maturalną w roku 1978.
Teoria liczb Konkurs prac uczniowskich
Skrót pracy nagrodzonej złotym medalem w konkursie Polskiego Towarzystwa Matematycznego i redakcji Delty na najlepszą pracę maturalną w roku 1978.
W 1964 roku amerykańsko-brytyjski matematyk Neil Sloane zaczął kolekcjonować znane ciągi liczb całkowitych. Niewinne hobby, motywowane zbadaniem własności kilku ciągów, które pojawiły się podczas pracy nad jego rozprawą doktorską, szybko przerodziło się w duże przedsięwzięcie. W efekcie zostały opublikowane dwie książki A Handbook of Integer Sequences (wydana w roku 1973, zawierająca 2372 ciągi) oraz The Encyclopedia of Integer Sequences (z 1995 roku, 5847 ciągi). W 1996 roku, gdy liczba zgromadzonych ciągów przekroczyła 10 000, dalsze ich przechowywanie w postaci książkowej stało się bardzo niepraktyczne...
Tak jak problemy praktyczne prowadzą do równań, tak równania prowadzą czasem do nowych rodzajów liczb. Ambitny kmieć z czasów Mieszka I, będący właścicielem trzech krów i marzący o nabyciu (lub zdobyciu) dodatkowych sztuk bydła tak, by stać się szanowanym posiadaczem tuzina krów, musiał niewątpliwie rozwiązywać zadanie matematyczne, które dziś zapisujemy równaniem 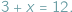 Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie
Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie 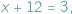 które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...
które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...
Do jednych z najstarszych problemów w historii matematyki należy niewątpliwie zaliczyć równania diofantyczne, czyli równania o dziedzinie rozwiązań ograniczonej do liczb całkowitych. Obecną nazwę zawdzięczają one Diofantosowi, greckiemu matematykowi żyjącemu w III wieku naszej ery w Aleksandrii. Swoje rozważania na temat takich równań Diofantos zawarł w serii ksiąg pod tytułem Arytmetyka. Studiując jedną z nich, Pierre de Fermat - żyjący w XVII wieku francuski prawnik i matematyczny samouk - uznał, że pewne zawarte w niej równanie nie może mieć rozwiązań, o czym raczył poinformować przyszłych czytelników w słynnej uwadze, zamieszczonej na marginesie (czytanej przezeń książki oraz niniejszego artykułu).

wikipedia
Carl Friedrich Gauss (1777-1855)
Rozwiązywanie równań wymuszało poszerzenie zasobu liczb, jakimi się posługiwano. Równanie 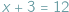 można było rozwiązać, posługując się najnaturalniejszymi liczbami, zwanymi zresztą naturalne, ale równanie
można było rozwiązać, posługując się najnaturalniejszymi liczbami, zwanymi zresztą naturalne, ale równanie 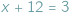 wymagało rozszerzenia ich zasobu do liczb całkowitych. Wyjście poza obręb równań pierwszego stopnia pokazało, że do rozwiązania np. równania
wymagało rozszerzenia ich zasobu do liczb całkowitych. Wyjście poza obręb równań pierwszego stopnia pokazało, że do rozwiązania np. równania 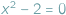 nie wystarczą nie tylko liczby całkowite, ale nawet wszystkie liczby wymierne, czyli ułamki
nie wystarczą nie tylko liczby całkowite, ale nawet wszystkie liczby wymierne, czyli ułamki 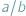 zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną
zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną 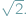
Gry, zagadki, paradoksy Mała Delta
"Matematyka wedyjska" to umowna nazwa zbioru algorytmów, które można zastosować, aby rozwiązać pewne rachunkowe problemy. Reguły te zostały sformułowane w XX wieku przez hinduskiego duchownego Bharatiego Kriszna Tirtha, który twierdził, że są one zapisane w hinduskich świętych księgach, Wedach.

W matematycznym świecie od zawsze znajdowało się mnóstwo tajemnic czekających na odkrycie. Tak zawiłych i zdradzieckich, że tylko szaleńcy mogli w ogóle wyobrazić sobie ich istnienie. Tymi szaleńcami byli nieustraszeni matematycy, którzy już od stuleci (jeżeli nie tysiącleci) szukają, rozwiązują i wyjaśniają zagadki, które większość ludzi już dawno uznawała za beznadziejne przypadki (lub są one tak abstrakcyjne, że w żaden sposób nieosiągalne).
Dotarliśmy do ostatniej części cyklu, w którym prezentujemy wybrane przykłady zaskakujących relacji pomiędzy różnymi, pozornie bardzo odległymi, obszarami matematyki. Nie wypada jednak zakończyć bez poświęcenia należytej uwagi dziedzinie teorii liczb. Jak bowiem matematyka nazywana jest często królową nauk, tak o teorii liczb mówi się często jako o królowej matematyki. A królowa ma, oczywiście, wielu służących.
- Z tymi ułamkami to zupełnie nic nie wiadomo - narzekał po lekcji matematyki Janek. - Na przyklad 
Rozważamy wielomian 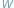 o współczynnikach rzeczywistych stopnia
o współczynnikach rzeczywistych stopnia 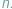 Wiadomo, że wielomian taki ma
Wiadomo, że wielomian taki ma 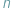 pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu
pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu 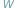 należących do wybranego przedziału
należących do wybranego przedziału 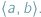 Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej
Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej 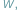 znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.
znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.

prof. dr Roman Sikorski (1920 - 1983) - polski matematyk, profesor Uniwersytetu Warszawskiego i Instytutu Matematycznego PAN.
Liczby naturalne są niewątpliwie naturalne. Liczby całkowite niewątpliwie zasługują na nazwę całkowite. Liczby wymierne należałoby możne nazywać liczbami mierzącymi lub wymierzającymi, bowiem wszystkie pomiary wykonujemy w praktyce w liczbach wymiernych, zresztą nie tylko pomiary: wszelkie rachunki na konkretnych liczbach wykonywane są w praktyce wyłącznie w obrębie liczb wymiernych. Po co więc wprowadzać szersze, lecz znacznie trudniejsze pojęcie liczb rzeczywistych, skoro liczby wymierne wystarczają w rachunkach? Definicja liczb rzeczywistych nastręcza zawsze pewne trudności, wskutek tego w podręcznikach szkolnych jest raczej przemycana, niż precyzyjnie formułowana.
Poniższe zadania łączy to, że do rozwiązania każdego z nich można użyć pewnego Bardzo Znanego Twierdzenia, udowodnionego całkiem niedawno. Oczywiście to, że można strzelać z armaty do muchy nie oznacza, że zawsze trzeba...
Nie ma słynniejszego twierdzenia niż Wielkie Twierdzenie Fermata (WTwF) i tego nie zamierzam tu dowodzić. Zacznę po prostu od sformułowania faktu, który od 1995 roku jest rzeczywiście twierdzeniem za sprawą Andrew Wilesa, a wcześniej przez około trzy i pół wieku był hipotezą zajmującą głowy największych matematyków i rzesze amatorów...
Jednym z najstarszych zagadnień matematyki są równania algebraiczne, wśród nich problem znalezienia pierwiastków trójmianu kwadratowego...
Czy jest coś weselszego na twarzy drugiego człowieka od jego uśmiechu? To w pewnym sensie filozoficzne pytanie potrafi wzbudzić wiele zainteresowania u każdego człowieka. Wszak każda osoba posiada swój własny kanon piękna oraz szczęścia...
W tym artykule ilustrujemy potęgę logarytmów w projektowaniu efektywnych algorytmów i obliczeń. Myślenie, w tle którego stoi logarytm, ukryty lub widoczny, nazwaliśmy myśleniem logarytmicznym. Stanowi ono jedną z podstawowych kompetencji niezbędnych przy efektywnym rozwiązywaniu rzeczywistych problemów informatycznych. Pokazujemy również - co może być ciekawe dla nauczycieli matematyki - jak wprowadzić pojęcie logarytmu, nie odwołując się do matematycznego formalizmu, a posługując się koncepcyjnym modelem redukcji rozmiaru problemu w każdym (lub w co drugim) kroku co najmniej o połowę. Może Cię zdziwić, że ta idea prowadząca do logarytmu występuje w algorytmie Euklidesa, który został opisany niemal 2000 lat przed wynalezieniem logarytmu przez Napiera.
Żonglerka to starożytna sztuka, jej początki wydają się dorównywać wiekiem ludzkości, znane są np. rysunki żonglującej kobiety znalezione w egipskim grobowcu datowanym na XII wiek p.n.e. Wystarczy kilka kamieni i trochę praktyki, nie jest więc wcale zdumiewające, że ludzie zaczęli się tym zajmować bardzo dawno.
Sztuka w trzech aktach z prologiem i epilogiem...
Starożytni Egipcjanie sprzed 4000 lat uznawali tylko ułamki proste, czyli takie, które w liczniku miały jedynkę. Oczywiście, były też inne ułamki, ale o nich uczeni mówić nie chcieli – przedstawiali je jako sumę ułamków prostych. Nie byłoby w tym niczego nadzwyczajnego, gdyby nie pretensjonalne wymaganie, aby w owej sumie każdy ułamek był inny.