Delta mi!

Podczas odbywającego się w 1900 roku w Paryżu Drugiego Międzynarodowego Kongresu Matematyków jeden z referatów wygłosił wybitny niemiecki matematyk David Hilbert. W swoim wystąpieniu zawarł on listę dwudziestu trzech zagadnień matematycznych stanowiących, jego zdaniem, szczególne wyzwanie dla matematyków w rozpoczynającym się XX wieku. Większość z nich doczekała się rozwiązania. Inne, jak słynna hipoteza Riemanna, pozostają otwarte, inspirując kolejne pokolenia naukowców.

O stosowaniu podstawowej wiedzy szkolnej na temat funkcji kwadratowej do rozwiązywania zadań olimpijskich.

Pokazy iluzjonistyczne nacechowane są elementami odwracającymi uwagę, nadzwyczajną zwinnością, sprawnością ruchową lub rachunkową iluzjonisty. Dla nas, matematyków, najciekawsze są oczywiście te wykorzystujące pewne aspekty matematyki. Przedstawimy kilka trików, które łączy wspólne ogniwo - systemy pozycyjne.

Tym razem o kilku ciekawych własnościach funkcji Eulera.

Kwadrat liczby rzeczywistej jest nieujemny (fanfary!).

O paru zasadach pozwalających stwierdzić, który z dwóch zbiorów ma więcej elementów, ale bez liczenia elementów tych zbiorów.

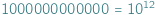Jednym z naturalnych skojarzeń z nieskończonością są duże, bardzo duże liczby. Tak bardzo, że trudno je sobie wyobrazić, a intuicja nie pomaga. Możemy jednak o nich pomyśleć. Czytając doniesienia o wydatkach z budżetu państwa lub tym bardziej o światowej gospodarce, łatwo pogubić się w milionach, miliardach i bilionach. I chociaż wiemy, że w bilionie mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.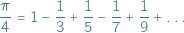

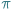Suma kwadratów najczęściej kojarzy się nam z twierdzeniem Pitagorasa - słusznie, ale warto wiedzieć, że temat ten ma swoje miejsce również w teorii liczb, gdzie interesuje nas, czy daną liczbę całkowitą można przedstawić w postaci sumy kwadratów innych liczb całkowitych. Intrygujące jest również pytanie, ile składników znajduje się w tej sumie. Osiągnięcia w tym zakresie mieli między innymi Fermat, Euler i Lagrange...

O wyrażeniach symetrycznych oraz uproszczeniach, które można stosować w rozwiązywaniu zadań z takimi wyrażeniami.

Powiążemy tu wzór Leibniza

z geometrią (pola) i teorią liczb. Tekst jest wyraźnie dłuższy od tego, który jest w książce Hilberta i Cohn-Vossena, bo szkicujemy dowód twierdzenia z teorii liczb, na które autorzy jedynie powołują się. Pozostawimy jednak bez dowodu niektóre bardzo znane twierdzenia z teorii liczb, ze względu na ograniczenia miejsca w miesięczniku. Zaznaczyć warto, że podawany zwykle studentom pierwszego roku dowód jest krótszy, ale zdaniem autora tego tekstu, nie pokazuje związku z geometrią, który jest mocno sugerowany obecnością we wzorze.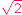

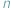Nieoczywiste zastosowania oczywistego stwierdzenia: pomiędzy dwiema kolejnymi liczbami całkowitymi nie ma żadnej liczby całkowitej.

Niech będzie liczbą nieparzystą...

Pierre de Fermat był Francuzem i żył w pierwszej połowie XVII wieku (1601-1665). Jako radca prawny praktykował w sądzie w Tuluzie na południu Francji. Naukami ścisłymi, a w szczególności matematyką, interesował się jako amator, ale wniósł potężny wkład do ich rozwoju. Szczególnie spektakularne są jego osiągnięcia w teorii liczb i o nich traktuje niniejszy artykuł. Wszyscy wiedzą, że jest Wielkie Twierdzenie Fermata (WTwF), Małe Twierdzenie Fermata (MTwF) i jeszcze inne twierdzenia Fermata dotyczące teorii liczb - ale które z nich jest największe?

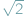Zupełnie nieszokująca zasada dobrego uporządkowania mówi, że każdy niepusty podzbiór liczb naturalnych ma element najmniejszy. Pokażemy, jak ją wykorzystać do wykazania, że jest niewymierne, czyli że dla żadnej liczby naturalnej 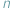liczba 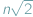nie jest całkowita.

Przy dzieleniu liczb wielocyfrowych metodą pisemną często wykonuje się następującą operację...

Praca nadesłana na Konkurs Prac Uczniowskich dotyczy nowej metody dowodzenia pewnych nierówności. W niniejszym skrócie umieszczam jedynie ważniejsze twierdzenia (bez dowodów) i niektóre ich zastosowania.

Nierówności między średnimi, a w szczególności nierówność między średnią arytmetyczną i geometryczną (oznaczana dalej A-G), to jedne z podstawowych narzędzi dowodowych w arsenale każdego olimpijczyka...

Pierwszy etap pitagoreizmu głosił hasło wszystko jest liczbą: pożądaną Harmonię Świata da się wyrazić jako stosunek liczb (dziś nazywanych naturalnymi), przy czym jest ona tym pełniejsza, im liczby te są mniejsze.

Skończyłam! - krzyknęła triumfalnie Agatka do swojego brata, Bartka. Dziewczynka regularnie domaga się od starszego chłopca rozmaitych ciekawostek matematycznych, których ten dowiaduje się w liceum...

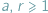Słynne twierdzenie Dirichleta głosi, że jeżeli liczby naturalne są względnie pierwsze, to ciąg arytmetyczny 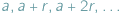zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.