Delta mi!

Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 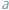i 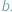Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach 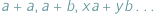Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów i a niektóre można otrzymać na wiele sposobów.

Na obrazku widać przenumerowanie szesnastu z 17 równo rozmieszczonych punktów na okręgu. Obok "normalnych" czarnych numerków podano dziwnie rozmieszczone czerwone. Zrobiono to w ten sposób, że nawinięto na ten okrąg półprostą, na której zaznaczono punkty odpowiadające kolejnym potęgom 3.

W 1994 roku Peter Shor, pracujący wówczas w Bell Labs w New Jersey, pokazał, jak przy użyciu hipotetycznego komputera kwantowego rozłożyć w czasie wielomianowym dowolną liczbę naturalną na czynniki pierwsze. W tamtym czasie algorytmy kwantowe dopiero raczkowały. To właśnie odkrycie Shora spowodowało wielki rozwój tej dziedziny. Społeczność informatyków zrozumiała, że gdyby udało się zbudować komputer kwantowy rozsądnej wielkości, to świat stałby się istotnie inny. Nie jest bowiem znany żaden algorytm dla problemu faktoryzacji, czyli rozkładu na dzielniki pierwsze, który działa w czasie wielomianowym na komputerze klasycznym. Co więcej, nawet nie znaleziono algorytmu losowego, który z dużym prawdopodobieństwem w zazwyczaj niedługim czasie faktoryzuje liczbę: nie jest po prostu znana zupełnie żadna rozsądna heurystyka...

Jeżeli określimy dodawanie i mnożenie punktów płaszczyzny, z wyróżnionymi punktami 0 i 1, w sposób przedstawiony na rysunku, to otrzymamy liczby zespolone...

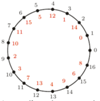
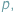W Delcie 7/2017 przedstawiliśmy kilka "olimpijskich" zastosowań twierdzenia Combinatorial Nullstellensatz. Okazuje się, że zamiast "zwykłych" wielomianów wielu zmiennych możemy rozważać wielomiany o współczynnikach będących resztami z dzielenia przez pewną liczbę pierwszą z dodawaniem i mnożeniem modulo 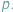Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.

O trudnym problemie, który ma jednozdaniowe rozwiązanie...

Kiedy miałem kilka, kilkanaście lat, wraz ze starszym bratem często graliśmy w grę. Należało w swojej kolejce podać liczbę większą od wskazanej przez poprzednika. Przegrywał oczywiście ten, kto nie był w stanie podać liczby większej. Czasami ponosiła nas fantazja i mówiliśmy "nieskończoność" albo "nieskończoność plus nieskończoność". Dziś już wiem, że nieskończoność liczbą nie jest, a działania na nieskończonościach są bardziej wyrafinowane, niż podejrzewałem. Gdyby i Tobie, drogi Czytelniku, przyszło kiedyś wymienić (albo usłyszeć) jakąś dużą liczbę, możesz sięgnąć do poniższej listy. Nie są to bowiem byle jakie liczby...

W historii ludzkiego poznania mało jest tak fascynujących pojęć jak liczby pierwsze. Chociaż dzisiaj wiemy o nich znacznie więcej niż 120 lat temu, to jeszcze więcej dotyczących ich pytań pozostaje bez odpowiedzi. Celem tej notki jest pokazanie, że trudno jest ocenić na pierwszy rzut oka, czy pytanie dotyczące liczb pierwszych jest łatwe, czy też bardzo trudne - poza zasięgiem współczesnej nauki.

W tym artykule chcemy zaprezentować pewną technikę dowodową zwaną interpretacją kombinatoryczną. Metoda ta pokazana będzie w działaniu: podajemy dwa zadania wraz z rozwiązaniami, które są ilustracją tematu.

Małe Twierdzenie Fermata ma również taki dowód...

Indukcja pozaskończona wykorzystywana jest w dowodach istnienia różnych obiektów matematycznych. Główną częścią tego typu dowodu jest definicja indukcyjna (inaczej: rekurencyjna) funkcji.

Udowodnijmy lub obalmy twierdzenie: istnieją takie liczby niewymierne i że jest liczbą wymierną.

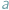
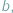
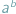
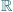Zbiór wszystkich liczb rzeczywistych nie jest równoliczny ze zbiorem wszystkich liczb naturalnych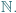

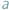Dawno, dawno temu, za drugą górą, za trzecią rzeką żył sobie królewicz Leonardo pochodzący ze szlachetnego rodu Fibonaccich. No, może nie całkiem królewicz, ale piąty syn dyplomaty włoskiego. Może nie całkiem za trzecią rzeką, bo urodził się za ósmą doliną i trzynastoma bagnami, dokładniej w Pizie w 1175 roku. Zatem przynajmniej rzeczywiście żył dawno, dawno temu. Choć w pewnym sensie żyje do dzisiaj w swoich uczniach, bowiem wieść o liczbach Fibonacciego rozeszła się po świecie i szumi o nich niejeden las...

Artykuł o powyższym tytule wypada rozpocząć od przypomnienia, czym są kongruencje. Jeśli dwie liczby naturalne i 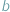dają tę samą resztę z dzielenia przez liczbę naturalną 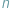(innymi słowy, jeśli jest podzielne przez 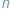), uczenie jest stwierdzić, że 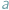i 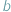przystają do siebie modulo 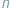i fakt ten zanotować jako 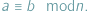W tym kontekście znaczek " " (lub raczej to, co on sobą reprezentuje) nazywamy właśnie kongruencją.

Jakie jest największe miasto na świecie? Czy wirus jest organizmem żywym? Jaki jest najpiękniejszy obraz Tycjana? Są to proste pytania, na które nie ma jednoznacznej odpowiedzi. Przyczyną jest brak jasno określonych kryteriów. Jedną z cech wyróżniających matematykę spośród innych dziedzin życia i nauki jest to, że każde pojęcie ma swoją precyzyjną definicję. Wydaje się więc, że na każde pytanie matematyczne jest jednoznaczna odpowiedź, którą można formalnie uzasadnić. W konsekwencji, nic nie jest brane "na wiarę". Okazuje się, że nie do końca tak jest!

Na drugim etapie tegorocznej Olimpiady Matematycznej pojawiło się pewne zadanie. Pojawiło się ono na zawodach z numerem 1 i (zgodnie z oczekiwaniami) okazało się bardzo łatwe - rozwiązała je znacząca większość uczestników. Przedstawimy szkic rozwiązania... x

Tak zwana zasada szufladkowa Dirichleta, jakże lubiana przez rozmaite komitety olimpiad matematycznych, łączy w sobie dwie atrakcyjne cechy. Z jednej strony jest tak prosta, że nawet dziecko w przedszkolu jest w stanie ją zrozumieć, z drugiej zaś zawiera zupełnie nieoczywisty element niekonstruktywny. Głosi ona mianowicie, że wkładając do szuflad więcej niż przedmiotów, mamy pewność, że w którejś szufladzie będą co najmniej dwa obiekty. W której - nie wiadomo, ale na pewno w którejś.