Funkcja 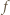 jest ciągła i rosnąca, a jej granice przy końcach dziedziny
jest ciągła i rosnąca, a jej granice przy końcach dziedziny 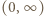 wynoszą 0 oraz
wynoszą 0 oraz 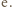 Zatem liczba
Zatem liczba 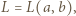 dla której
dla której 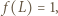 jest jednoznacznie określona. Wykażemy, że
jest jednoznacznie określona. Wykażemy, że 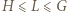 (gdzie
(gdzie 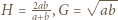 ); stąd też wyniknie, że
); stąd też wyniknie, że 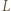 leży pomiędzy
leży pomiędzy 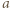 i
i 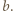 Wobec ścisłej monotoniczności funkcji
Wobec ścisłej monotoniczności funkcji 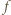 wystarczy dowieść, że
wystarczy dowieść, że 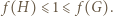
Niech 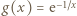 dla
dla 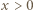 ; jest to funkcja rosnąca. Skoro
; jest to funkcja rosnąca. Skoro 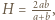 zatem
zatem
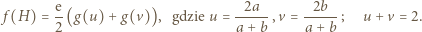 |
(1) |
Badając znak 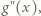 stwierdzamy, że funkcja
stwierdzamy, że funkcja 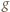 jest wklęsła w przedziale
jest wklęsła w przedziale 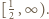 Jeżeli więc liczby
Jeżeli więc liczby 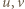 leżą w tym przedziale, to
leżą w tym przedziale, to 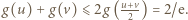 Jeśli zaś np.
Jeśli zaś np. 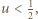 rozważamy dwa podprzypadki (pamiętając, że
rozważamy dwa podprzypadki (pamiętając, że 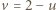 ):
):
we wszystkich przypadkach uzyskane wartości nie przekraczają 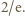 Otrzymane oszacowanie
Otrzymane oszacowanie 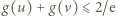 pokazuje (zgodnie ze wzorem (1)), że
pokazuje (zgodnie ze wzorem (1)), że 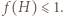
Pozostało do wykazania, że 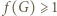 ; do tego użyjemy funkcji
; do tego użyjemy funkcji 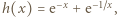 bowiem
bowiem
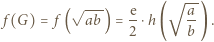 |
(2) |
Nietrudno się przekonać, że dla 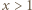 zachodzi nierówność
zachodzi nierówność 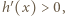 czyli
czyli 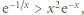 równoważna (przez logarytmowanie) nierówności
równoważna (przez logarytmowanie) nierówności 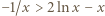 ; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie
; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie 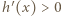 dla
dla 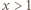 ; stąd
; stąd 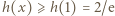 dla
dla 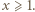 Ponieważ bez straty ogólności można przyjąć, że
Ponieważ bez straty ogólności można przyjąć, że 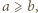 ze wzoru (2) wnosimy, że
ze wzoru (2) wnosimy, że 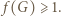 To kończy rozwiązanie.
To kończy rozwiązanie.
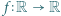 ma tę własność, że każda z funkcji
ma tę własność, że każda z funkcji 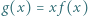 oraz
oraz 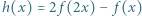 ma granicę 0 przy
ma granicę 0 przy 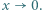 Czy wynika stąd, że także funkcja
Czy wynika stąd, że także funkcja 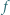 ma granicę 0 przy
ma granicę 0 przy 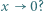
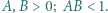
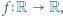
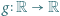
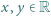

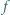
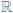
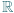 ; ma więc funkcję odwrotną
; ma więc funkcję odwrotną 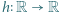
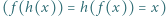 . Udowodnić, że funkcja
. Udowodnić, że funkcja 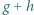
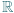
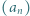 jest określony wzorami
jest określony wzorami 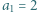 ;
; 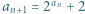 dla
dla 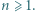 Niech
Niech 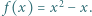 Udowodnić, że dla każdego
Udowodnić, że dla każdego 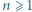 liczba
liczba 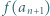 dzieli się przez
dzieli się przez 
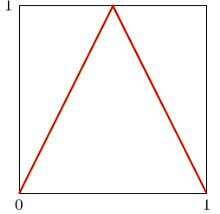
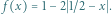
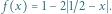
![| f [0,1] [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/1x-6ef1c75cd7890fac5a5a10e6c2a3afccfa359dba-im-2C,6B,73-FF,FF,FF.gif) będzie dane wzorem
będzie dane wzorem 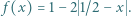 Niech ponadto
Niech ponadto 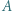 oraz
oraz 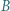 będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie
będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie 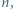 że
że 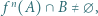 gdzie
gdzie 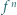 oznacza
oznacza  -krotne złożenie funkcji
-krotne złożenie funkcji 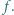
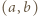 ma tę własność, że
ma tę własność, że ![fn((a,b)) = [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/2x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) dla pewnego
dla pewnego 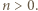 Niech
Niech 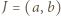 i
i 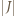 będzie długością tego przedziału. Zauważmy, że jeżeli
będzie długością tego przedziału. Zauważmy, że jeżeli 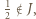 to
to 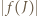 jest przedziałem dwukrotnie dłuższym niż
jest przedziałem dwukrotnie dłuższym niż 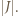 Tym samym kolejne przekształcenia
Tym samym kolejne przekształcenia 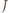 przez
przez 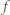 są przedziałami długości
są przedziałami długości 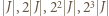 i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy
i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy 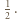 Wobec powyższego istnieje takie
Wobec powyższego istnieje takie 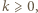 że
że 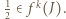 Ale
Ale 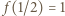 i
i 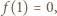 czyli
czyli 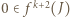 i wobec tego
i wobec tego 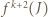 jest przedziałem postaci
jest przedziałem postaci 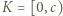 dla pewnego
dla pewnego 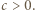 Teraz
Teraz 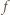 ponownie podwaja długość przedziału
ponownie podwaja długość przedziału 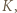 wobec tego dla pewnego
wobec tego dla pewnego 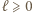 zachodzi
zachodzi 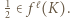 Tym samym
Tym samym ![[0, | 1/2]⊂ fℓ(K)](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/25x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) i wystarczy jeszcze zauważyć, że
i wystarczy jeszcze zauważyć, że![[0,1] = f ([0,1/2]) ⊂ fℓ+1(K) = fℓ+1( fk+2(J)) = fk+ℓ+3(J).](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/26x-3582530a21981c4662de24aae4547af0402ec105-dm-66,57,43-FF,FF,FF.gif)
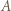 postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli
postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli 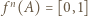 z przypadku ogólnego, to tym bardziej
z przypadku ogólnego, to tym bardziej 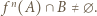
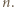
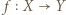 nazywamy iniekcją (funkcją różnowartościową), jeśli z warunku
nazywamy iniekcją (funkcją różnowartościową), jeśli z warunku 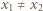 wynika, że
wynika, że 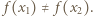 Funkcję
Funkcję 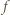 nazywamy surjekcją (funkcją na), gdy dla dowolnego
nazywamy surjekcją (funkcją na), gdy dla dowolnego 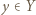 istnieje
istnieje 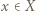 takie, że
takie, że 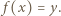 Funkcja, która jest jednocześnie iniekcją i surjekcją, to bijekcja.
Funkcja, która jest jednocześnie iniekcją i surjekcją, to bijekcja.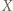 jest skończony, gdy istnieje liczba
jest skończony, gdy istnieje liczba 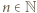 oraz bijekcja między zbiorami
oraz bijekcja między zbiorami 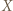 oraz
oraz 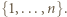 Piszemy wtedy również
Piszemy wtedy również 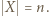
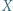 będzie zbiorem skończonym. Udowodnić, że dowolna iniekcja
będzie zbiorem skończonym. Udowodnić, że dowolna iniekcja 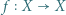 jest bijekcją.
jest bijekcją.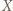 oraz
oraz 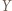 są zbiorami skończonymi o tej samej liczbie elementów oraz
są zbiorami skończonymi o tej samej liczbie elementów oraz 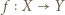 jest iniekcją, to
jest iniekcją, to 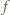 jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę
jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę 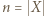 elementów zbioru
elementów zbioru 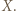 Oczywiście przypadek
Oczywiście przypadek 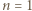 jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech
jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech 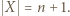 Niech
Niech 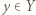 będzie takie, że
będzie takie, że 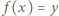 dla pewnego
dla pewnego 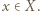 Takie
Takie 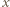 jest jedyne na mocy iniektywności, zatem można rozważyć funkcję
jest jedyne na mocy iniektywności, zatem można rozważyć funkcję 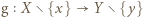 daną wzorem
daną wzorem 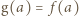 dla
dla 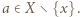 Wtedy
Wtedy 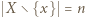 oraz
oraz 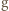 jest iniekcją. Istotnie, jeżeli
jest iniekcją. Istotnie, jeżeli 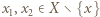 i
i 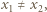 to
to 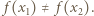 Zauważmy teraz, że
Zauważmy teraz, że 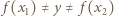 (ponownie korzystamy z iniektywności), zatem również
(ponownie korzystamy z iniektywności), zatem również 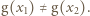 Tym samym
Tym samym 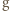 jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że
jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że 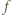 jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
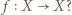 Usunięcie jednego elementu z dziedziny i przeciwdziedziny nie gwarantuje, że dziedzina i przeciwdziedzina
Usunięcie jednego elementu z dziedziny i przeciwdziedziny nie gwarantuje, że dziedzina i przeciwdziedzina 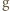 będą tym samym zbiorem, a tylko wtedy moglibyśmy skorzystać z założenia indukcyjnego!
będą tym samym zbiorem, a tylko wtedy moglibyśmy skorzystać z założenia indukcyjnego!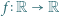 spełniające dla wszystkich
spełniające dla wszystkich 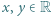 nierówność
nierówność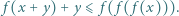
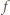 spełnia warunki zadania. Niech
spełnia warunki zadania. Niech 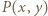 oznacza nierówność
oznacza nierówność 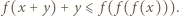 Wybierzmy dowolnie
Wybierzmy dowolnie 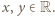 Ponieważ
Ponieważ 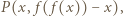 więc
więc 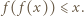 Podstawiając w ostatniej nierówności
Podstawiając w ostatniej nierówności 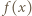 zamiast
zamiast  i uwzględniając
i uwzględniając 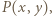 dostajemy
dostajemy 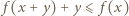 dla dowolnych
dla dowolnych 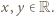 Podstawiając
Podstawiając 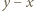 zamiast
zamiast 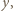 dostajemy
dostajemy 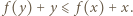 Z dowolności
Z dowolności 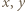 wnioskujemy, że
wnioskujemy, że 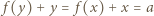 dla pewnego
dla pewnego 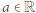 i wszystkich
i wszystkich 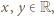 zatem musi być
zatem musi być 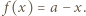 Łatwo sprawdzić, że ta funkcja faktycznie spełnia
Łatwo sprawdzić, że ta funkcja faktycznie spełnia 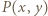 dla wszystkich
dla wszystkich 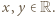
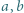 określamy funkcję
określamy funkcję 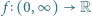 wzorem
wzorem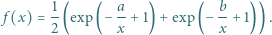
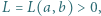 dla której
dla której 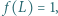 i że
i że 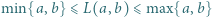 ; zatem liczba
; zatem liczba 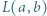 może być uważana za pewną średnią liczb
może być uważana za pewną średnią liczb 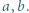
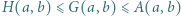 między średnimi: harmoniczną, geometryczną i arytmetyczną liczb
między średnimi: harmoniczną, geometryczną i arytmetyczną liczb 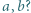
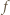 jest ciągła i rosnąca, a jej granice przy końcach dziedziny
jest ciągła i rosnąca, a jej granice przy końcach dziedziny 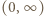 wynoszą 0 oraz
wynoszą 0 oraz 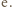 Zatem liczba
Zatem liczba 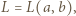 dla której
dla której 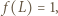 jest jednoznacznie określona. Wykażemy, że
jest jednoznacznie określona. Wykażemy, że 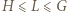 (gdzie
(gdzie 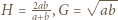 ); stąd też wyniknie, że
); stąd też wyniknie, że 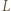 leży pomiędzy
leży pomiędzy 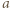 i
i 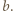 Wobec ścisłej monotoniczności funkcji
Wobec ścisłej monotoniczności funkcji 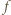 wystarczy dowieść, że
wystarczy dowieść, że 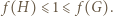
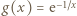 dla
dla 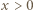 ; jest to funkcja rosnąca. Skoro
; jest to funkcja rosnąca. Skoro 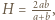 zatem
zatem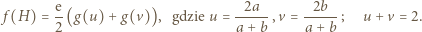
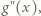 stwierdzamy, że funkcja
stwierdzamy, że funkcja 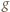 jest wklęsła w przedziale
jest wklęsła w przedziale 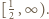 Jeżeli więc liczby
Jeżeli więc liczby 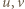 leżą w tym przedziale, to
leżą w tym przedziale, to 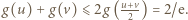 Jeśli zaś np.
Jeśli zaś np. 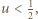 rozważamy dwa podprzypadki (pamiętając, że
rozważamy dwa podprzypadki (pamiętając, że 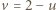 ):
):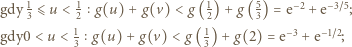
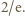 Otrzymane oszacowanie
Otrzymane oszacowanie 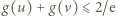 pokazuje (zgodnie ze wzorem (1)), że
pokazuje (zgodnie ze wzorem (1)), że 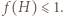
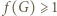 ; do tego użyjemy funkcji
; do tego użyjemy funkcji 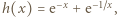 bowiem
bowiem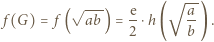
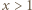 zachodzi nierówność
zachodzi nierówność 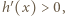 czyli
czyli 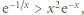 równoważna (przez logarytmowanie) nierówności
równoważna (przez logarytmowanie) nierówności 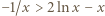 ; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie
; tę ostatnią nierówność sprawdzamy bez trudu, przenosząc wszystko na jedną stronę i ponownie różniczkując. Zatem istotnie 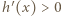 dla
dla 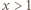 ; stąd
; stąd 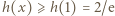 dla
dla 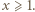 Ponieważ bez straty ogólności można przyjąć, że
Ponieważ bez straty ogólności można przyjąć, że 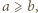 ze wzoru (2) wnosimy, że
ze wzoru (2) wnosimy, że 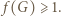 To kończy rozwiązanie.
To kończy rozwiązanie.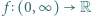 jest dana wzorem
jest dana wzorem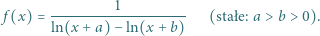
 ), i znaleźć równanie tej asymptoty.
), i znaleźć równanie tej asymptoty.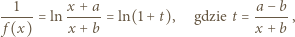
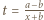 dąży do 0, gdy
dąży do 0, gdy 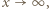 zatem
zatem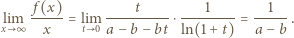
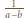 ; wystarczy zatem, by następująca różnica miała skończoną granicę (przy
; wystarczy zatem, by następująca różnica miała skończoną granicę (przy 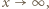 czyli
czyli 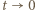 ):
):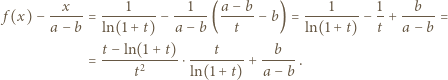
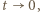 pierwszy z ilorazów (w ostatnim uzyskanym wyrażeniu) dąży do granicy 1/2 (bo
pierwszy z ilorazów (w ostatnim uzyskanym wyrażeniu) dąży do granicy 1/2 (bo 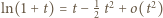 ). Stąd wniosek, że asymptotą (przy
). Stąd wniosek, że asymptotą (przy  ) jest prosta o równaniu
) jest prosta o równaniu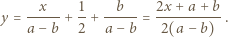
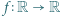 spełniające równanie
spełniające równanie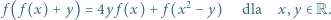
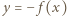 oraz
oraz 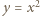 ; otrzymujemy równania
; otrzymujemy równania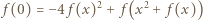
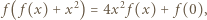
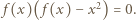 Zatem dla każdej liczby
Zatem dla każdej liczby 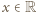 ma miejsce alternatywa:
ma miejsce alternatywa: 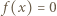 lub
lub 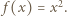 Stąd, w szczególności,
Stąd, w szczególności, 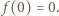
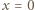 jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 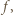 to
to 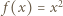 dla wszystkich
dla wszystkich  Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy
Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy 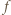 ma jeszcze jakieś miejsce zerowe
ma jeszcze jakieś miejsce zerowe 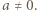 Wykażemy, że wówczas
Wykażemy, że wówczas 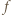 jest tożsamościowo równa zeru.
jest tożsamościowo równa zeru.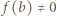 dla pewnego
dla pewnego 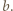 Biorąc w zadanym równaniu
Biorąc w zadanym równaniu 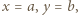 dostajemy
dostajemy 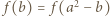 ; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie
; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie 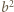 oraz
oraz 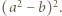 Przyrównanie tych wartości daje równość
Przyrównanie tych wartości daje równość 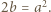 To liczba dodatnia; stąd
To liczba dodatnia; stąd 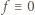 w przedziale
w przedziale ![|(−∞ ,0].](/math/temat/matematyka/analiza/zadania/2019/10/31/zm-k44-789/9x-86016eea9da0a9d7e7b58d20a6007ab7e898b219-im-66,57,43-FF,FF,FF.gif) Weźmy teraz dowolną liczbę
Weźmy teraz dowolną liczbę 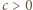 i w wyjściowym równaniu podstawmy
i w wyjściowym równaniu podstawmy 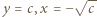 (już wiemy, że
(już wiemy, że 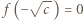 ). Wychodzi
). Wychodzi 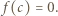 Tak więc
Tak więc 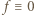 także w przedziale
także w przedziale 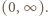
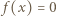 (dla wszystkich
(dla wszystkich 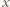 ) oraz
) oraz  (dla wszystkich
(dla wszystkich  ).
).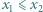 i
i 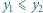 spełniają równości
spełniają równości 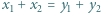 oraz
oraz 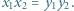 Udowodnić, że
Udowodnić, że 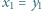 i
i 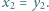
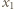 i
i 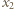 są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby
są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby 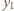 oraz
oraz 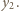
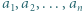 będą ustalonymi liczbami rzeczywistymi. Dla jakiego
będą ustalonymi liczbami rzeczywistymi. Dla jakiego 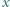 wartość funkcji
wartość funkcji
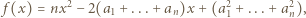
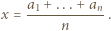
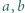 i
i  spełniają nierówność
spełniają nierówność 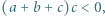 przy czym
przy czym 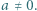 Wykazać, że
Wykazać, że 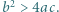
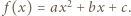 Wówczas mamy
Wówczas mamy 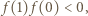 więc funkcja
więc funkcja 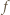 przyjmuje zarówno dodatnie i ujemne wartości, skąd
przyjmuje zarówno dodatnie i ujemne wartości, skąd 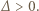
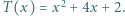
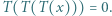
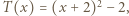
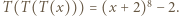
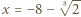
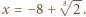
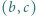
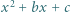
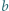
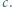
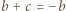
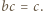
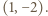


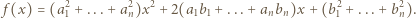
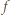 przyjmuje wyłącznie wartości nieujemne, więc
przyjmuje wyłącznie wartości nieujemne, więc 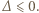 Jest to nierówność równoważna dowodzonej.
Jest to nierówność równoważna dowodzonej.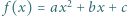 spełnia dla każdego
spełnia dla każdego ![|x∈ [−1,1]](/math/temat/matematyka/analiza/zadania/2019/09/30/zm-19_10-kpo-8/2x-74a6438c69d0f6ea8ca78cf3a770b01ff3c09138-im-2C,6B,73-FF,FF,FF.gif) nierówność
nierówność 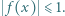 Wyznaczyć największą możliwą wartość wyrażenia
Wyznaczyć największą możliwą wartość wyrażenia 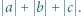
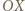 i
i 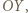 można założyć bez utraty ogólności, że
można założyć bez utraty ogólności, że 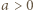 i
i 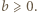 Jeśli
Jeśli 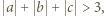 to
to 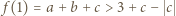 oraz
oraz 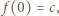 więc
więc 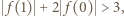 czyli
czyli 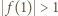 lub
lub 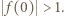 Wartość
Wartość 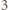 jest osiągalna, na przykład dla funkcji
jest osiągalna, na przykład dla funkcji 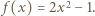
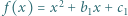 i
i 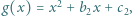 których współczynniki są rzeczywiste i spełniają warunek
których współczynniki są rzeczywiste i spełniają warunek
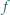 i
i 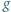 mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.
mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.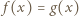 ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie 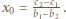 Wówczas
Wówczas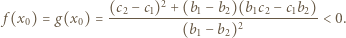
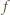 i
i 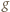 przecinają się tylko w jednym punkcie, leżącym poniżej osi
przecinają się tylko w jednym punkcie, leżącym poniżej osi 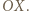 Resztę załatwia własność Darboux.
Resztę załatwia własność Darboux.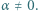 Funkcja
Funkcja 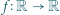 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 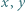 równanie
równanie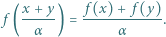
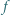 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 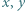 równanie
równanie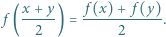
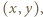 a drugi raz dla
a drugi raz dla 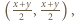 uzyskujemy
uzyskujemy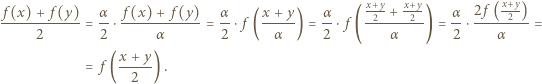
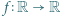 spełnia dla każdego
spełnia dla każdego 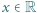 równość
równość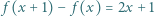
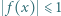 dla
dla ![x ∈[0,1].](/math/temat/matematyka/analiza/zadania/2018/12/30/zm-1588/5x-eccb368b79dc42272c83d4b8f232df0149187364-im-2C,6B,73-FF,FF,FF.gif) Wykazać, że
Wykazać, że 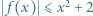 dla każdego
dla każdego 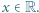
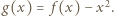 Wówczas
Wówczas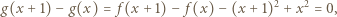
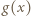 jest okresowa z okresem
jest okresowa z okresem 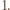 Skoro
Skoro 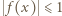 dla
dla ![|x∈ [0,1],](/math/temat/matematyka/analiza/zadania/2018/12/30/zm-1588/6x-d73afcece697591998b8c7aa137d57ff409fefb6-im-66,57,43-FF,FF,FF.gif) to
to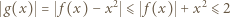
![x ∈ [0,1]](/math/temat/matematyka/analiza/zadania/2018/12/30/zm-1588/8x-d73afcece697591998b8c7aa137d57ff409fefb6-im-66,57,43-FF,FF,FF.gif) i w konsekwencji, wobec okresowości
i w konsekwencji, wobec okresowości 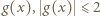 dla każdego
dla każdego 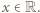 Stąd ostatecznie
Stąd ostatecznie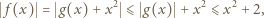
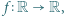 spełniające równanie
spełniające równanie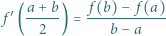
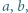 których różnica jest liczbą całkowitą.
których różnica jest liczbą całkowitą.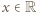 uzyskujemy z podanego równania (po podstawieniu
uzyskujemy z podanego równania (po podstawieniu 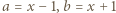 ) równość
) równość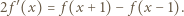
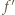 jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując
jest różniczkowalna. Możemy więc zróżniczkować (1) stronami, otrzymując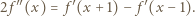
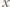 przez
przez 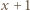 oraz
oraz 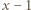 :
: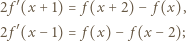
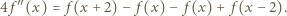
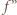 ma pochodną. Różniczkujemy (3) stronami:
ma pochodną. Różniczkujemy (3) stronami: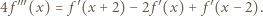
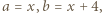 następnie
następnie 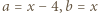 i wreszcie
i wreszcie 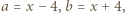 otrzymując kolejno
otrzymując kolejno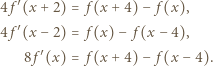
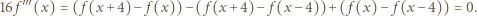
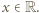 To znaczy, że
To znaczy, że 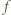 jest wielomianem stopnia najwyżej drugiego.
jest wielomianem stopnia najwyżej drugiego.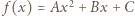 spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb
spełnia równanie dane w założeniu zadania (i to nawet dla każdej pary różnych liczb 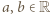 ) - co łatwo sprawdzić.
) - co łatwo sprawdzić.