Klub 44M - zadania XI 2020»Zadanie 809
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2020
- Publikacja w Delcie: listopad 2020
- Publikacja elektroniczna: 1 listopada 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (364 KB)
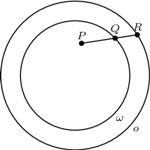
W trójkącie ostrokątnym 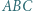 wysokości
wysokości 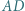 i
i 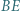 przecinają się w punkcie
przecinają się w punkcie 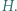 Proste
Proste 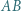 i
i 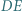 przecinają się w punkcie
przecinają się w punkcie 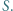 Prosta przechodząca przez środek
Prosta przechodząca przez środek 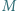 boku
boku 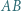 i równoległa do dwusiecznej kąta
i równoległa do dwusiecznej kąta 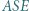 przecina proste
przecina proste 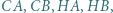 odpowiednio, w punktach
odpowiednio, w punktach 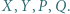 Udowodnić, że okręgi opisane na trójkątach
Udowodnić, że okręgi opisane na trójkątach 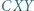 i
i 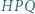 są przystające.
są przystające.

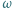
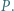
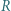
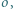
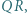
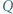
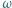
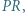

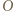
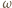
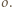
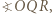
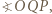
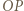
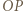
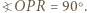
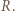
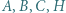
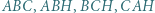
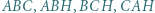
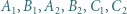
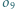
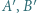
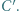
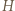 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 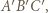 a dwusieczne kątów wewnętrznych i zewnętrznych przecinają okrąg opisany na trójkącie w środkach odpowiednich łuków (zob. kącik nr 3).
a dwusieczne kątów wewnętrznych i zewnętrznych przecinają okrąg opisany na trójkącie w środkach odpowiednich łuków (zob. kącik nr 3).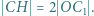
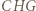 i
i 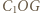 są podobne (kk).
są podobne (kk).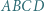
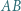
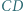
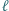
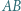
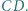
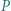
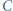
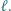
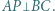
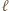 jest prostą Eulera trójkąta
jest prostą Eulera trójkąta 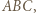 bo leży na niej środek ciężkości i środek okręgu opisanego na tym trójkącie. Punkt
bo leży na niej środek ciężkości i środek okręgu opisanego na tym trójkącie. Punkt 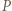 jest ortocentrum trójkąta
jest ortocentrum trójkąta 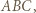 gdyż leży on na jego prostej Eulera oraz na wysokości poprowadzonej z wierzchołka
gdyż leży on na jego prostej Eulera oraz na wysokości poprowadzonej z wierzchołka 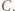
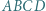
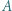
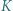
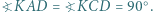
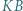
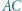
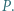
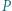
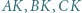
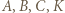 tworzą układ ortocentryczny, gdyż
tworzą układ ortocentryczny, gdyż 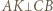 i
i 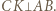
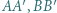
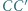
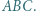
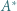
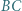
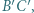
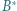
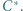
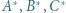
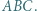
 względem okręgów:
względem okręgów: 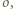 okręgu o średnicy
okręgu o średnicy 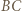 oraz
oraz 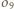 są równe, więc punkt
są równe, więc punkt 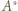 leży na osi potęgowej okręgów
leży na osi potęgowej okręgów  i
i 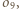 czyli prostej prostopadłej do
czyli prostej prostopadłej do 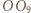 (prostej Eulera). Analogicznie postępujemy z punktami
(prostej Eulera). Analogicznie postępujemy z punktami 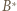 i
i 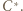 (O potędze punktu względem okręgu można przeczytać w kąciku nr 11).
(O potędze punktu względem okręgu można przeczytać w kąciku nr 11).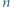 -kąta
-kąta 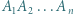 leży taki punkt
leży taki punkt 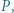 że każdy z trójkątów
że każdy z trójkątów 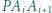 jest równoramienny (przyjmujemy
jest równoramienny (przyjmujemy 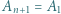 ). Czy stąd wynika, że wielokąt ma okrąg opisany, którego środkiem jest punkt
). Czy stąd wynika, że wielokąt ma okrąg opisany, którego środkiem jest punkt 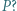
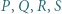 tworzą układ ortocentryczny, to:
tworzą układ ortocentryczny, to: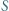 względem prostej
względem prostej 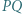 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 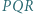 ;
;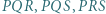 i
i 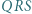 mają równe promienie;
mają równe promienie;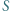 względem środka odcinka
względem środka odcinka 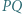 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 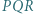 ;
;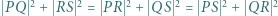 ;
;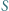 jest środkiem okręgu wpisanego lub dopisanego do trójkąta utworzonego przez spodki układu.
jest środkiem okręgu wpisanego lub dopisanego do trójkąta utworzonego przez spodki układu.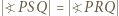 lub
lub 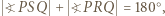 w zależności od umiejscowienia punktu
w zależności od umiejscowienia punktu 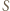 względem pozostałych.
względem pozostałych.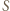 i
i 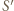 są symetryczne względem prostej
są symetryczne względem prostej 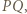 to okręgi opisane na trójkątach
to okręgi opisane na trójkątach 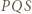 i
i 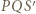 również. Wystarczy skorzystać z poprzedniego podpunktu.
również. Wystarczy skorzystać z poprzedniego podpunktu.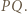
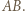 Okrąg o średnicy
Okrąg o średnicy 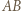 przecina proste
przecina proste 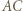 i
i 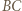 w punktach, które są spodkami wysokości trójkąta
w punktach, które są spodkami wysokości trójkąta 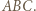
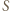 wewnątrz i na zewnątrz trójkąta
wewnątrz i na zewnątrz trójkąta 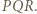 Do rachunków na kątach wykorzystać okręgi, o których była mowa we wstępie.
Do rachunków na kątach wykorzystać okręgi, o których była mowa we wstępie.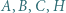 tworzą układ ortocentryczny, jeśli:
tworzą układ ortocentryczny, jeśli: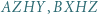 i
i 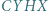 są rombami (kolejność wierzchołków niekoniecznie podana antyzegarowo);
są rombami (kolejność wierzchołków niekoniecznie podana antyzegarowo);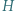 przechodzą trzy okręgi o jednakowych promieniach, a punkty
przechodzą trzy okręgi o jednakowych promieniach, a punkty 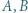 i
i 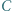 są różnymi od
są różnymi od 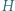 punktami przecięć tych okręgów;
punktami przecięć tych okręgów;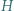 jest środkiem okręgu wpisanego w pewien trójkąt, a punkty
jest środkiem okręgu wpisanego w pewien trójkąt, a punkty 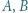 i
i 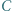 - środkami okręgów dopisanych do niego.
- środkami okręgów dopisanych do niego.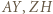 i
i 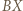 są równej długości i równoległe, więc czworokąt
są równej długości i równoległe, więc czworokąt 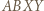 jest równoległobokiem. Mamy więc
jest równoległobokiem. Mamy więc 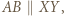 ale też
ale też 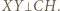
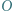 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 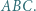 Punkty
Punkty 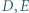 i
i 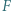 są symetryczne do punktu
są symetryczne do punktu 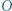 względem prostych odpowiednio
względem prostych odpowiednio 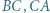 i
i 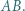 Dowieść, że punkt
Dowieść, że punkt 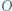 jest ortocentrum trójkąta
jest ortocentrum trójkąta 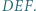
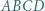 jest wpisany w okrąg. Punkty
jest wpisany w okrąg. Punkty 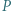 i
i 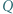 są ortocentrami trójkątów odpowiednio
są ortocentrami trójkątów odpowiednio 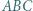 i
i 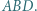 Udowodnić, że
Udowodnić, że 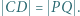
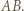 Okrąg o średnicy
Okrąg o średnicy 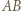 przecina proste
przecina proste 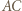 i
i 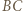 w punktach, które są spodkami wysokości trójkąta
w punktach, które są spodkami wysokości trójkąta 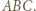
 i
i 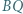 są wysokościami trójkąta nieprostokątnego
są wysokościami trójkąta nieprostokątnego 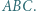 Punkty
Punkty 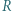 i
i 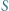 są rzutami prostokątnymi punktów odpowiednio
są rzutami prostokątnymi punktów odpowiednio 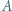 i
i 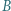 na prostą
na prostą 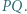 Udowodnić, że
Udowodnić, że 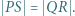

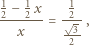
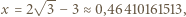 czyli stosunek pola kwadratu do pola trójkąta wynosi
czyli stosunek pola kwadratu do pola trójkąta wynosi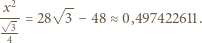
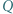 zawarty jest wielokąt o największym możliwym polu, podobny do danego wielokąta wypukłego
zawarty jest wielokąt o największym możliwym polu, podobny do danego wielokąta wypukłego 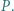 Jaką część pola
Jaką część pola 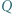 zajmuje ten wielokąt?
zajmuje ten wielokąt?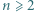 punktów czarnych i
punktów czarnych i 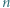 białych. Rysujemy
białych. Rysujemy 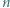 cięciw, z których każda ma jeden koniec biały a drugi czarny. Udowodnić, że można zrobić to tak, by każde dwie narysowane cięciwy przecinały się.
cięciw, z których każda ma jeden koniec biały a drugi czarny. Udowodnić, że można zrobić to tak, by każde dwie narysowane cięciwy przecinały się. cięciw "byle jak" i zastosować rozumowanie podobne do tego, które przedstawiono we wstępie.
cięciw "byle jak" i zastosować rozumowanie podobne do tego, które przedstawiono we wstępie.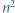 płytek w kształcie trójkąta równobocznego o boku 1 ułożono trójkąt równoboczny o boku
płytek w kształcie trójkąta równobocznego o boku 1 ułożono trójkąt równoboczny o boku 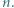 Każda płytka jest z jednej strony czerwona, a z drugiej niebieska. Ruch polega na wykonaniu następujących czynności: wybieramy płytkę
Każda płytka jest z jednej strony czerwona, a z drugiej niebieska. Ruch polega na wykonaniu następujących czynności: wybieramy płytkę 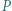 mającą wspólne boki z co najmniej dwiema płytkami, których widoczne strony mają kolor inny niż widoczna strona płytki
mającą wspólne boki z co najmniej dwiema płytkami, których widoczne strony mają kolor inny niż widoczna strona płytki  Następnie odwracamy płytkę
Następnie odwracamy płytkę  na drugą stronę. Czy ta zabawa może trwać bez końca?
na drugą stronę. Czy ta zabawa może trwać bez końca?