Delta mi!

W geometrii dyskretnej przyjęło się mówić, że wielokąt jest wpisany w inny wielokąt, gdy ma wierzchołki na prostych zawierających boki tego drugiego wielokąta. Od czasu Hilberta tego zwrotu używa się i w przypadku "zwyczajnej" geometrii.

...z których żadne dwie nie są równoległe, a żadne trzy nie mają punktu wspólnego... tworzą cztery trójkąty - to każdy widzi i nikt się nie dziwi.

Odcinek 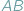widać z punktu 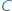pod kątem 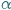, gdy 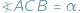Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 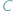i 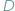leżą na okręgu po tej samej stronie jego cięciwy 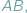to widać ją z 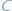i 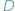pod tym samym kątem (Rys. 1).

Każdy zna twierdzenie o kącie zewnętrznym trójkąta: jest on równy sumie kątów wewnętrznych do niego nie przyległych (Rys. 1), co bierze się z faktu, że suma kątów przyległych jest równa sumie kątów trójkąta. Z twierdzenia tego wynika nietrudno twierdzenie o kącie wpisanym i środkowym: kąt wpisany jest równy 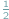kąta środkowego opartego na tym samym łuku.

Fakt (*). W trójkącie prostokątnym środek przeciwprostokątnej jest równo odległy od wierzchołków. Również na odwrót, jeśli środek okręgu opisanego leży na boku trójkąta, to trójkąt ten jest prostokątny.

Jeśli chcemy wyznaczyć długość pewnej krzywej lub łamanej, często warto ją rozwinąć albo w inny sposób rozprostować.

Dany jest okrąg...

Gdy na lustrzaną sferę pada promień światła, odbija się on tak, że kąt między nim a przedłużeniem promienia sfery przechodzącego przez punkt, w którym promień pada, jest równy kątowi między tym przedłużeniem a promieniem odbitym, przy czym wszystko odbywa się w jednej płaszczyźnie wyznaczonej przez padający promień i środek sfery. Geometrycznie sytuacja jest więc dwuwymiarowa.

W dowolnym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku i dwukrotnie od niego krótszy. Ten prosty fakt okazuje się zadziwiająco przydatny.

Tym razem będziemy wycinać...

Twierdzenie Talesa dowieść można bez trudu...

Panuje przekonanie, że w niemodnej obecnie dziedzinie geometrii klasycznej wszystko jest znane i nie pozostało nic do odkrycia. Kłam temu stwierdzeniu zadaje dość ciekawe i (jeszcze) mało znane twierdzenie, które przedstawiamy w niniejszym artykule. Warto zaznaczyć, że środki, jakie posłużyły nam do dowodu, są czysto geometryczne i nie korzystają z narzędzi analitycznych. Aby ułatwić jego zrozumienie, przedstawiamy najpierw pewne pojęcia, definicje i bardziej znane fakty powiązane z tym zagadnieniem.

W niniejszym artykule przybliżymy własności jednej z najsłynniejszych prostych w geometrii euklidesowej - prostej Simsona. Jej odkrycie przypisywane jest szkockiemu matematykowi, Robertowi Simsonowi, choć w żadnej jego pracy nie znajdujemy wzmianki o niej.

Problem, który opiszę, został zaproponowany przez Amerykanów na LV Międzynarodową Olimpiadę Matematyczną, a jego treść brzmi następująco...

Gwiazdka foremna to łamana zamknięta, wpisana w okrąg i złożona z jednakowej długości cięciw, ale niebędąca wielokątem foremnym. Nie trzeba długo się zastanawiać, by stwierdzić, że odcinki takich łamanych muszą się przecinać.

Na pierwszym etapie XI Olimpiady Matematycznej Gimnazjalistów pojawiło się pytanie, na które tylko 24% uczestników odpowiedziało poprawnie...

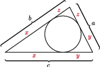
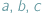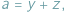
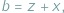
Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków pewnego trójkąta, często przydaje się podstawienie Raviego: 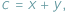gdzie 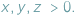Takie liczby 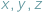zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.

Euklides w Elementach pisał: "... kwadrat jest tym, co równoboczne i prostokątne...". Oto kilka niebanalnych obserwacji, w których kwadrat jest jednym z bohaterów.