Delta mi!

Chociaż są to pojęcia abstrakcyjne (bo przecież nikt nie widział ani punktu, ani odcinka), przemawiają dobrze do wyobraźni i zgadzają się ze zdrowym rozsądkiem. I aż dziw bierze, jak wiele wokół nas zjawisk, które zdają się ostrzegać: uwaga to co wydaje się takie oczywiste, wcale nie musi być prawdziwe.

W artykule tym pragnę omówić pewne pojęcia, należące całkowicie do zakresu geometrii elementarnej, a dotąd niemal wcale nie zbadane. Jak wiadomo, dwa wielokąty 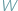i 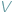nazywamy równoważnymi, wyrażając to wzorem: 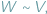jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...

Rozpatrzmy dowolny trójkąt oraz cztery kwadraty zbudowane w sposób przedstawiony na rysunku 1. Wówczas zaznaczone kolorem trzy odcinki, łączące odpowiednie wierzchołki kwadratów oraz środek najniższego kwadratu, przecinają się w jednym punkcie.

W 1641 roku ukazały się Centrobaryca Paula Guldina, a w nich twierdzenie znane dziś jako reguły Guldina...

...a pięciokąt foremny można. Obok pokazana jest konstrukcja dziesięciokąta foremnego - kolorowy odcinek ma długość boku dziesięciokąta foremnego wpisanego w większy okrąg, a więc biorąc co drugi z wierzchołków takiego dziesięciokąta, otrzymamy pięciokąt foremny. Konstrukcja jest - jak widać - bardzo prosta. Ma tylko tę wadę, że nie wskazuje, jak konstruować inne wielokąty foremne.

Z twierdzeniem Pitagorasa wszyscy się znamy, budowanie kwadratów na bokach trójkąta prostokątnego nie jest niczym nadzwyczajnym. A co możemy powiedzieć ciekawego o prostokątach skonstruowanych na bokach dowolnego trójkąta?

Twierdzenie o stycznej i cięciwie jest niezwykle prostym, a zarazem ogromnie przydatnym faktem z elementarnej geometrii...

W LXVI Olimpiadzie Matematycznej uczestniczyło 895 uczniów, więc aż o 272 osoby mniej niż rok wcześniej, do zawodów stopnia drugiego zakwalifikowano 409 uczniów, a do zawodów stopnia trzeciego -126 uczniów. Wiele osób, w tym niżej podpisany, uznało, że zadania domowe były za trudne i nie zachęcały uczniów spoza szkół o dużych tradycjach olimpijskich (a raczej uczniów nauczycieli, którzy uczą matematyki, a nie tylko przygotowują do zdania matury) do startowania w tych zawodach.

W każdym zjawisku przyrody można dostrzec dążenie do osiągnięcia jakiegoś maksimum lub minimum. Umiejętność wyznaczania wartości ekstremalnych nie powinna więc być niczym niezwykłym...

Jednym z najstarszych zagadnień matematyki są równania algebraiczne, wśród nich problem znalezienia pierwiastków trójmianu kwadratowego...

Jedną z najsłynniejszych niemożliwych rzeczy w matematyce jest konstrukcja samym cyrklem i linijką kwadratu o polu równym polu danego koła. Problem ten, zwany kwadraturą koła, rozważano już w starożytnej Grecji, ale rozwiązano go, czyli udowodniono niekonstruowalność, dopiero w XIX wieku.

Przeciętny uczeń rozpoczyna podróż po fascynującym świecie geometrycznych konstrukcji uzbrojony w linijkę i kątomierz. Kiedy już nauczyciel uzna swojego podopiecznego za wystarczająco odpowiedzialnego, by nie rysował szkolnych ławek (jakże często zbyt naiwne założenie), uczeń dostaje do ręki kolejne narzędzie walki z czystą kartką papieru, jakim jest cyrkiel...

Dawno, dawno temu za górami, za lasami na Euklidesowych Równinach żyło sobie koło. Niezmiernie było dumne ze swej stałej szerokości. Chadzało ścieżkami, które miały szerokość równą jego średnicy, i jako jedyna figura zamieszkująca równiny mogło kręcić się przy tym jak szalone, stale podpierając obie krawędzie ścieżki.

Istnieje zaskakujący związek między okręgiem wpisanym w trójkąt i okręgiem na nim opisanym.

Zechciejcie państwo wysłuchać dziś krótkiej opowieści z królestwa geometrii. Za siedmioma górami matematycznych podręczników, za siedmioma rzekami matematycznych równań, za siedmioma lasami matematycznych sprzeczności znajdowała się symediana. Dziś symediana ujrzy światło dzienne...

Zająłem się ciekawym problemem dotyczącym centrów trójkąta. Ciekawym, bo łatwym do wyobrażenia, a w pewnych aspektach nawet bardzo trudnym.

Tym razem o twierdzeniu Pascala...

Wiele wzorów na sumy kolejnych liczb naturalnych, ich kwadratów, sześcianów itp. można uzasadnić (lub przynajmniej przekonująco zilustrować) na rysunkach. Często rysunki te wymagają niewiele lub nawet zero komentarza – są to tzw. dowody bez słów...

W naszych rozważaniach wzbogacimy płaszczyznę o dodatkowy punkt, który oznaczymy przez 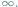 Przyjmiemy przy tym, że ów punkt leży na każdej z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną nazwą bloków...