Delta mi!

W jednej z historii "z brodą" opowiada się, jak to pewien profesor egzaminując studenta z fizyki zapytał...

W temperaturze pokojowej gaz, zbiór atomów czy cząsteczek, a także powietrze, którym oddychamy, z powodzeniem można sobie wyobrażać jako rój maleńkich obiektów, niemal doskonałych punktów materialnych, poruszających się z prędkościami rzędu kilkuset kilometrów na godzinę i od czasu do czasu zderzających się zupełnie jak kule bilardowe. Oczywiście, różne atomy poruszają się w gazie z różnymi prędkościami. Odpowiedni rozkład prawdopodobieństwa występowania prędkości znamy jako rozkład Maxwella. Typowa, lub lepiej, średnia prędkość atomów maleje wraz z obniżaniem temperatury gazu proporcjonalnie do pierwiastka kwadratowego z temperatury bezwzględnej.

Czym jest sekunda? Dlaczego jej długość ciągle się zmienia? Jak działa zegar atomowy? Dlaczego pojedynczy pomiar sekundy może trwać kilkanaście minut? I dlaczego ostatecznie nigdy nie znamy aktualnego czasu?2

Wśród pytań, które zawsze absorbowały ludzkość, na plan pierwszy wybija się: co to jest życie? Zadają sobie to pytanie ludzie młodzi, zadają lekarze, filozofowie, fizycy, biolodzy. Każdy odpowiada na to pytanie nieco inaczej, po swojemu. Biolodzy, jako ci, którzy zajmują się studiowaniem istot żywych, wydają się szczególnie predestynowani do szukania odpowiedzi...

Każdy z nas przychodząc na świat, a właściwie należałoby powiedzieć: zasiadając na ławie szkolnej, zastaje pewien obraz nauk, które w sposób mniej lub bardziej schematyczny dzielą między siebie dotychczasowy dorobek myśli ludzkiej. Dowiadujemy się na przykład, że równia pochyła i kalorymetr - to fizyka, natomiast sole i kwasy - to chemia, a pływak żółtobrzeżek i moczarka kanadyjska - to biologia. Oczywiście później przekonujemy się, że fizyka, w odróżnieniu od Coca-Coli, "to nie jest to", lecz znacznie, znacznie więcej. Podobnie jest i z innymi naukami...

Jednym z podstawowych wzorów trygonometrycznych jest twierdzenie kosinusów podające zależność między bokami trójkąta a jednym z jego kątów: 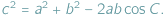Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt 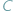jest prosty, czyli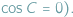

Każda nauka ścisła ma własne metody potwierdzania swoich tez. Dla większości z nich weryfikacja twierdzeń polega na konfrontacji z rzeczywistością. Matematyka jest jedyną z tych nauk, w której owa rzeczywistość nie jest ostateczną (ani jakąkolwiek) metodą sprawdzania zdań aspirujących do wzbogacenia zasobu wiedzy matematycznej. Weryfikatorem twierdzeń jest dowód. Mowa tu o tzw. matematyce czystej lub teoretycznej; zauważmy jednak, że fizyczna rzeczywistość weryfikuje stosowalność instrumentów matematycznych, nie ich wartość matematyczną.

Liczby naturalne są niewątpliwie naturalne. Liczby całkowite niewątpliwie zasługują na nazwę całkowite. Liczby wymierne należałoby możne nazywać liczbami mierzącymi lub wymierzającymi, bowiem wszystkie pomiary wykonujemy w praktyce w liczbach wymiernych, zresztą nie tylko pomiary: wszelkie rachunki na konkretnych liczbach wykonywane są w praktyce wyłącznie w obrębie liczb wymiernych. Po co więc wprowadzać szersze, lecz znacznie trudniejsze pojęcie liczb rzeczywistych, skoro liczby wymierne wystarczają w rachunkach? Definicja liczb rzeczywistych nastręcza zawsze pewne trudności, wskutek tego w podręcznikach szkolnych jest raczej przemycana, niż precyzyjnie formułowana.

Pytanie postawione w tytule można rozumieć dwojako: po pierwsze - co chcielibyśmy rozumieć przez cząstkę elementarną, a po drugie - co dziś obejmujemy tą nazwą. W pierwszym znaczeniu chodziłoby więc o podanie definicji, która by mogła nam dostarczyć kryterium rozpoznawania cząstek elementarnych, w drugim zaś o ustalenie stanu faktycznego, do którego doszło w wyniku wieloletnich badań teoretycznych i eksperymentalnych.

7 października 2135 roku Księżyc na 4 minuty i 43 sekundy przesłoni Słońce i większość terytorium naszego kraju na chwilę ogarnie ciemność. Wcześniej zdarzą się zaćmienia częściowe. Wszystkich zaćmień Słońca, widocznych w różnych częściach świata, będą w bieżącym tysiącleciu setki i szczegółowy przebieg każdego z nich można przewidzieć na kilkaset lat do przodu. Jak to się dzieje, że potrafimy tak precyzyjnie te zjawiska przewidywać?

Z czym kojarzy się Monte Carlo? Z kasynami, hazardem, ruletką. A więc Monte Carlo jest symbolem potęgi przypadku, który jednym pozwala zbijać fortuny, innych rujnuje. Są jednak ludzie, którzy przypadkowość, losowość potrafią okiełznać i wykorzystać z pożytkiem (przynajmniej dla siebie). Oczywiście, takimi ludźmi są właściciele kasyn gry, ale nie tylko. Również matematycy zaprzęgają losowość do pożytecznej roboty. Metody obliczeniowe oparte na generowaniu (symulowaniu komputerowym) zdarzeń losowych nazywają się... oczywiście, metodami Monte Carlo.

Marian Ritter von Smolan Smoluchowski - światowej sławy polski fizyk, pionier fizyki statystycznej, alpinista i taternik, żył w latach 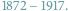Egzopeptydazy to specjalny typ enzymów. Co może mieć wspólnego Smoluchowski z egzopeptydazami, skoro ani on, ani nikt z jego współczesnych nie wiedzieli o ich istnieniu? I co do tego mają grafy? Postaram się wszystko wyjaśnić w odpowiedniej kolejności. Zacznę od uproszczonego modelu fizycznego. Podobno zbliżony model rozpatrywał Smoluchowski, ale, niestety, nie udało mi się dotrzeć do źródeł i sprawdzić tej informacji.

Emitery światła oparte na azotku galu (GaN) rewolucjonizują codzienne życie. Dzięki niebieskim laserom azotkowym Blu-ray czterokrotnie zwiększyła się gęstość optycznego zapisu danych. Gdy włączamy telewizor, cieszy nas wysoka jakość obrazu i odwzorowanie kolorów, możliwe dzięki nowoczesnym wyświetlaczom z podświetleniem diodowym. Od kilku lat powszechne stają się mikroprojektory, oparte na bardzo jasnych, półprzewodnikowych źródłach światła. Poszerzają się też możliwości diagnostyki medycznej czy komunikacji podwodnej dzięki laserom emitującym światło zielone 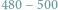nm. Wszystko to zawdzięczamy kryształowi azotku galu, który określany jest jako półprzewodnik przyszłości.

Bryła to stworzenie, z którym większość z nas poznała się w szkole podstawowej i które było przez nas oswajane przez kolejne lata edukacji. Znamy bliżej różne rodziny brył, takie jak wielościany, graniastosłupy, bryły obrotowe, foremne, platońskie. Oczywiście, można produkować nowe stworzenia, łącząc czy tnąc "podstawowe" gatunki, a jedynym ograniczeniem jest nasza wyobraźnia.

Legenda głosi, że historia kondensacji Bosego-Einsteina rozpoczęła się przypadkiem, podczas wykładu na Uniwersytecie w Dhace. Prowadzący, Satyendra Nath Bose, pokazywał, że współczesny mu statystyczny opis teorii promieniowania ciała doskonale czarnego nie zgadza się z obserwacjami. Jednak podczas wyprowadzenia popełnił elementarny "błąd" - potraktował cząstki jako obiekty nierozróżnialne. Konsekwencją jego błędu była całkowita zgodność teorii i doświadczenia. Pewne jest, że w czerwcu 1924 roku Bose napisał do Alberta Einsteina list z prośbą o ocenę swego artykułu na temat nowego wyprowadzenia rozkładu Plancka. Artykuł, uprzednio odrzucony przez czasopisma naukowe, został przetłumaczony przez Einsteina na język niemiecki i za jego rekomendacją opublikowany.

Zasada szufladkowa Dirichleta jest w anglojęzycznym świecie spopularyzowana jako pigeonhole principle: po włożeniu trzech gołębi do dwóch przegródek w którejś z przegródek będą co najmniej dwa gołębie.

O tym, co zdaniem niektórych wynika z faktu istnienia życia na Ziemi oraz o braku dowodów na istnienie życia na Marsie i innych ciekawostkach przyrodniczych...

Etap rozwoju cywilizacyjnego można poznać po ilości i rodzaju śmieci, które dana cywilizacja po sobie zostawia. Obecny przełom tysiącleci to epoka tworzyw sztucznych. Ich dostępność i trwałość zmieniły nasze zwyczaje i zapewnią nam nieśmiertelność: [...] trza dzieciom ostawić długi. Wielgie długi, co by je spłacały. Bedóm długo spłocać, bedóm długo wiedzieć, ze miały ojca. (Józef Tischner, Historia filozofii po góralsku).

Pioruny kuliste są zjawiskami efemerycznymi, jak na razie skutecznie unikającymi ostatecznego wyjaśnienia ich natury. Jest kilka konkurencyjnych teorii. Wszystkie one mogą być poprawne, bo podobnie mogą wyglądać pioruny kuliste o różnych mechanizmach powstawania, ale równie dobrze wszystkie mogą być częściowo lub całkowicie chybione.

W Delcie była już mowa o ruchomych wielościanach, nazywanych też fleksorami; artykuły o nich ukazały się w 1987 i 1997 roku. Ruchomość wielościanu polega na tym, że gdybyśmy zbudowali model o sztywnych ścianach, a krawędziach poruszających się jak zawiasy, to moglibyśmy nim poruszać bez odkształcania ścian. Choć wydaje się to zaskakujące, ruchome wielościany rzeczywiście istnieją i zbudowanie takich brył, choćby z papieru, nie jest bardzo trudne.

W Delcie 6/2011 artykuł Marii Donten-Bury o płaszczyźnie rzutowej został poprzedzony przedstawieniem sześciu jej (płaszczyzny, nie Marysi) postaci, pod jakimi daje się nam ona zaobserwować. Wobec tego, że postacie te są bardzo różnorodne, nasunąć się może wątpliwość, czy faktycznie wszystkie są wcieleniami tego samego matematycznego obiektu. Poniżej jest przedstawiony sposób, jak tę wątpliwość można rozstrzygnąć.

Nie kto inny, ale Albert Einstein określił kiedyś fizykę jako naukę opierającą swe teorie na pomiarach, której idee dają się sformułować za pomocą matematyki. Że opis ten jest trafny, pokazuje historia największych odkryć naukowych o charakterze teoretycznym, którym niemal zawsze towarzyszyły także przełomy w technikach pomiarowych używanych przez uczonych. Jeśli jednak zastanowić się głębiej, cytat ten traci swą elegancką ogólność, gdy zastosować go do jednej z fundamentalnych dziedzin fizyki – mechaniki kwantowej. Jak bowiem, mierząc coś, sprawdzać teorię, która sama definiuje, czym właściwie jest pomiar?

Pamięci ulotne umożliwiające zarówno zapis, jak i odczyt danych, nazywane są tradycyjnie pamięciami o dostępie swobodnym (ang. Random Access Memory). W komputerach stosuje się je jako element pośredni pomiędzy szybkimi rejestrami procesora a wolnymi dyskami twardymi. Jak zobaczymy, również pamięci RAM dzielą się na dwie główne kategorie: szybkie i drogie pamięci statyczne (ang. Static RAM) oraz wolniejsze i tańsze pamięci dynamiczne (ang. Dynamic RAM).

Zanim coś połkniemy, warto sprawdzić, czy aby to coś nie jest większe od nas...

W 1933 roku Fritz Zwicky, badając prędkości galaktyk w gromadzie Warkocza Bereniki, uzyskał wyniki wskazujące na obecność w tej gromadzie znacznie większej ilości materii niż ta, którą było widać. Była to pierwsza ze wskazówek, że we Wszechświecie może być dużo czegoś, czego zobaczyć się nie da!

Wszyscy wiemy, że wiele problemów nie daje się rozwiązać za pomocą komputera tylko z powodu ich zbyt dużej „złożoności obliczeniowej”. Pod tym poważnym stwierdzeniem kryje się prosta i smutna prawda. Nawet najszybsze komputery są zbyt wolne, aby uporać się z niejednym zadaniem. Wiemy też, że nie da się w nieskończoność zwiększać szybkości komputerów. Rozmiary atomów wyznaczają możliwą do wyobrażenia skalę miniaturyzacji. Jako że żaden sygnał nie może rozchodzić się szybciej niż światło w próżni, czas potrzebny na przesłanie informacji między fragmentami procesora też jest ograniczony od dołu. Czy komputer kwantowy może stać się remedium na powyższy problem?

Sieci optyczne są nowym materiałem, będącym cały czas przedmiotem aktywnych badań. W ostatnich latach bardzo szybko pojawiają się nowe możliwości eksperymentalne, rozwijana jest teoria. Można je zastosować do badania mechanizmów fizyki ciała stałego.

Formułując szczególną teorię względności (STW) Einstein nie używał pojęcia czasoprzestrzeni – zbioru zdarzeń, operował oddzielnie pojęciami czasu i przestrzeni. Pojęcie czasoprzestrzeni pojawiło się podczas odczytu wygłoszonego w 1908 roku przez Hermanna Minkowskiego w Kolonii. Minkowski pokazał, że do opisu STW wygodnie jest posługiwać się szczególną czterowymiarową geometrią, nazwaną później jego nazwiskiem.

Postęp w technice nie może odbywać się bez nowych technologii. Wielkie epoki w historii cywilizacji nazwane zostały od materiałów, które ludzie nauczyli się obrabiać i wykorzystywać (co często wiązało się z wynalezieniem nowych technik produkcji) – epoka kamienia, brązu, żelaza, pary. Nie wiemy jeszcze, pod jaką nazwą w historii znajdzie się przełomowy wiek XX – czy będzie to wiek krzemu, elektroniki czy informatyki.

W numerze poświęconym mierze (8/2008) nie sposób pominąć tych pierwszych, czyli zwykłych miar geometrycznych (zważmy, że geometria ma miarę w swojej nazwie).Wydaje się, że wiemy o nich wszystko, bo przecież stykaliśmy się z nimi niemal od zerówki. Okazuje się jednak, że i na ich temat można postawić pytania o nieoczywistych odpowiedziach.

Także w świecie komputerów posługujemy się różnymi miarami. Podstawową jednostką mierzącą ilość danych jest bajt (B).

Układ kwantowy jest opisywany tak zwanym stanem kwantowym układu – jest to obiekt matematyczny zawierający pełną informację o układzie. Nie wszystkie parametry opisywane przez stan kwantowy mogą być zmierzone – te, które da się wyznaczyć za pomocą pomiaru, nazywa się obserwablami.

Korzenie teorii miary sięgają tak podstawowych pojęć, jak długość (np. odcinka), pole (np. koła) i objętość (np. kuli). Wraz z rozwojem matematyki konieczne stało się uogólnienie tych pojęć w taki sposób, żeby dało się „zmierzyć” coraz bardziej skomplikowane podzbiory danej przestrzeni – na przykład prostej rzeczywistej 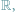do której w tym artykule ograniczymy nasze rozważania.

Jak wiadomo, komputery traktują wszystkie dane, na których działają, jako ciągi bitów, z których każdy może mieć dwie wartości (0 lub 1). Przykładowo, ten tekst jest zapisany w ten sposób, że każdej z liter i pozostałych znaków odpowiada ciąg 8 bitów. Daje to 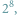czyli 256 możliwości, co w zupełności wystarcza do zapisania wszystkich potrzebnych znaków. Jednak w rzeczywistości różnych znaków występujących w tekście jest mniej. Problem jest więc taki: jak zapisać tekst tak, żeby na każdą jego literę przypadało jak najmniej bitów?

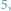
Jednym z podstawowych sposobów mierzenia zbioru jest liczenie jego elementów. Liczenie ma jednak jasny sens tylko dla zbiorów skończonych. Wiadomo, co to znaczy, że jakiś zbiór ma 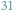czy 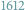elementów. W przypadku zbiorów nieskończonych sytuacja jest natomiast znacznie mniej oczywista. Czy zbiorowi nieskończonemu da się w ogóle przypisać liczbę elementów sensowniej niż przez uznanie, że wynosi ona zawsze ?

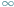Czy zastanawiałeś się, drogi Czytelniku, dlaczego wyszukiwarka wyświetla adresy stron będących odpowiedzią na Twoje zapytanie właśnie w takiej, a nie innej kolejności?

Prawie dwieście lat temu Augustin Cauchy udowodnił, że wielościan wypukły, który ma sztywne ściany, jest cały sztywny, choćby jego krawędzie były wyposażone w najlepsze zawiasy. I postawił problem, czy założenie wypukłości jest konieczne.

Lato to dla mieszczuchów okazja do oglądania zachodów Słońca. Nic, w zasadzie, nie stoi na przeszkodzie podziwianiu również wschodów. Sprzyja temu urlop nad morzem albo, jeszcze lepiej, rejs jachtem. Przy odrobinie szczęścia, któremu odrobina wiedzy nie zaszkodzi, można wtedy zaobserwować tytułowe zjawisko.

---

Przedstawione tu wyprowadzenie prawa równoważności, dotychczas nigdzie nie publikowane, ma dwie zalety. Chociaż wykorzystuje się w nim szczególną zasadę względności, nie wymaga to jednak stosowania formalnego aparatu teorii.

W marcu 1905 r. A.Einstein wysłał do publikacji pracę [Annalen der Physik 17, 132 (1905)], którą jako jedyną w swym dorobku uznał za "bardzo rewolucyjną".

Historia ruchów Browna jest niezwykle pasjonująca. Jest to historia zmagań mających na celu wyjaśnienie tajemniczego zjawiska, jakie odkrył w 1827 roku szkocki botanik Robert Brown.

Spośród trzech słynnych prac, które 26-letni Albert Einstein opublikował w czsopiśmie "Annalen der Physik" w 1905 roku największą karierę poza fizyką, w świadomości ogółu wykształconych ludzi, zrobiła zapewne ta z numeru 17, o krótkim tytule "O elektrodynamice ciał w ruchu". Praca zawiera wykład teorii przestrzeni, czasu i zjawisk elektromagnetycznych, którą potem, za Maxem Planckiem, nazwano szczególną teorią względności.

Wyobraźmy sobie małe, senne miasteczko na rubieży kresów, zamieszkane przez 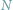osób...

Trudności z poprawnym zdefiniowaniem prędkości pokonał dopiero Newton wprowadzając rachunek różniczkowy. Wcześniej „straszyło” widmo aporii Zenona z Elei, który poddawał w wątpliwość istnienie ruchu pokazując, że przyjęcie jego realności prowadzi do sprzeczności. Najbardziej znane z tych aporii to „Achilles i żółw”, oraz „strzała”.

Ogólna teoria względności nauczyła nas, że geometria jest nieodłączną częścią współczesnej fizyki. W teorii tej Albert Einstein wskazał geometrii miejsce równoważne temu, które zajmuje materia. Sprawił, że ta pierwsza stała się obiektem dynamicznym i zaczęto pytać o jej ewolucję i kształt.