Delta mi!

SF w tytule nie oznacza Science Fiction, jak można by podejrzewać. Chcemy mówić o zjawiskach niemających charakterystycznej dla siebie skali czy rozmiaru. Zjawiska te noszą angielską nazwę Scale Free i stąd pochodzi akronim użyty w tytule. Rozczarowanych wypada przeprosić, ale i zaprosić do dalszej lektury, która będzie przedziwną mieszanką faktów z różnych dziedzin wiedzy, w tym także spoza nauk potocznie zwanych ścisłymi.

O tym, że świerszcz piszczy w trawie wiedzą wszyscy. O tym, że zimno to brak ciepła, również. Ale czy wszyscy wiedzą, czym tak naprawdę jest ciepło? Co właściwie o nim wiemy?

Jedną z konsekwencji teorii względności Einsteina jest wzrost bezwładności ciał w ruchu. W skrócie, im szybciej porusza się ciało, tym trudniej jest zmienić jego prędkość. Ponieważ wielkością będącą miarą bezwładności w fizyce jest masa, kuszącym pomysłem jest, aby tłumaczyć ten efekt wzrostem masy właśnie. Wiele materiałów dotyczących Szczególnej Teorii Względności wprowadza wobec tego podział na "masę spoczynkową", czyli masę, którą ciało ma w bezruchu, i "masę relatywistyczną", czyli masę ciała w ruchu, większą od spoczynkowej...

W matematyce często rozróżnia się rzeczy liniowe od nieliniowych. W szkole uczy się o funkcjach liniowych i nieliniowych, ale te pojęcia są dużo szersze i oprócz teorii dotyczą także wielu sytuacji praktycznych. Układ liniowy można przeanalizować w ten sposób, że rozkłada się go na części, analizuje działanie każdej z nich osobno, a na końcu dodaje do siebie poszczególne wyniki. W układzie nieliniowym taka analiza może dać niepoprawne wyniki.

Jądra atomowe składają się z protonów i neutronów, określanych zbiorczo mianem nukleonów. Nukleony wyobrażamy sobie zazwyczaj jako cząstki złożone z trzech kwarków, utrzymywanych razem przez oddziaływania silne. W odróżnieniu od oddziaływań elektromagnetycznych, w oddziaływaniach silnych mamy do czynienia nie z jednym, ale z trzema ładunkami. Fizycy nazywają te ładunki ładunkami kolorowymi, posuwając się niekiedy do nazywania ich określonymi kolorami: czerwonym, zielonym i niebieskim. Nie mają one, rzecz jasna, nic wspólnego z jakimkolwiek zmysłowym postrzeganiem barw i stanowią zaledwie metaforę dla pewnych struktur matematycznych.

W kwietniu 2019 roku mieliśmy okazję zobaczyć pierwszy obraz supermasywnej czarnej dziury w centrum galaktyki M87, zarejestrowany przez Teleskop Horyzontu Zdarzeń (Event Horizon Telescope, EHT). Obraz przedstawia niezbyt ostry jasny pierścień, czasem określany jako cień czarnej dziury. Szybko zrobił popkulturową karierę, zostając bohaterem licznych memów, ale czy aby wszyscy publikujący jego internetowe przeróbki wiedzą, co tak naprawdę przedstawia? Żeby to wyjaśnić, musimy najpierw cofnąć się w czasie o 100 lat, do początków teorii względności i teorii grawitacyjnego ugięcia promieni światła.

Tak zwana ciemna materia jest jedną z największych zagadek nie tylko współczesnej astronomii, ale także fizyki. Jest potrzebna do wyjaśnienia obserwacji astronomicznych, na przykład krzywych rotacji galaktyk, które kręcą się tak, jakby znajdowały się w potencjale grawitacyjnym tworzonym przez coś więcej niż tylko widoczną, świecącą materię gwiazd i gazu. Ciemna materia z definicji nie emituje fal elektromagnetycznych, oddziałuje natomiast grawitacyjnie...

Człowiek to istota nie tylko myśląca, ale i mierząca - można by rzec górnolotnie, że mierzenie (rozmiarów wrogiej armii, zaopatrzenia spichrzów, stanu skarbca itp.) leży u podstaw naszej cywilizacji. W języku matematyki miara jest definiowana przez następujące, zdroworozsądkowe warunki...

W końcu 2016 roku sąd okręgowy stanu Wisconsin po raz pierwszy w historii wyborów do Kongresu USA zdecydował o zmianie dystryktów wyborczych. Uzasadnieniem było to, że jednomandatowe dystrykty wyborcze dawały niesprawiedliwą przewagę Republikanom. Zdaniem sądu partia ta, mając przewagę w kongresie stanowym, po spisie powszechnym 2010 roku wyznaczyła dogodny dla siebie układ dystryktów.

Widmo spektroskopowe światła widzialnego - szerzej znane jest jako… tęcza. Na pozornie białe światło słoneczne składa się cała paleta barw - od czerwonego do fioletowego. Ale czym tak naprawdę są te kolory? To sposób, w jaki nasz mózg interpretuje różne długości fali promieniowania elektromagnetycznego (światła). Czerwony kolor to najdłuższe fale, jakie potrafi rejestrować nasze oko, a fioletowy to te najkrótsze.

Już od XIX wieku wiadomo, że każdy pierwiastek układu okresowego emituje i absorbuje światło tylko na określonych długościach fali (patrz artykuł powyżej). Astronomowie zauważyli jednak, że dla gwiazd i galaktyk linie widmowe często są przesunięte w stosunku do tych laboratoryjnych, mimo że odległości pomiędzy poszczególnymi liniami pozostają niezmienne. Dla większości galaktyk przesunięcie to następuje w kierunku dłuższych długości fali, czyli w stronę koloru czerwonego. Dlatego zjawisko to nazwano przesunięciem ku czerwieni (redshift). W astronomii często jest oznaczane literą z.

Drugą zasadę termodynamiki kojarzymy z nieodwracalnością procesów fizycznych, "strzałką czasu", entropią i jej nieuchronnym wzrostem.

Powszechnie znana podręcznikowa odpowiedź na pytanie, ile jest oddziaływań fundamentalnych, brzmi: cztery.

Jak mierzyć trudność problemów? Trudność albo, inaczej mówiąc, ich skomplikowanie, złożoność. To nie jest łatwe pytanie. Aby móc na nie chociaż nieco sensownie odpowiedzieć, skupimy się tu na tzw. problemach decyzyjnych, czyli takich, na które odpowiedź zawsze brzmi "tak" lub "nie". Żeby określić, jak złożone są te problemy, przyjmuje się zasadę, że problem jest tak trudny, jak jego najlepsze rozwiązanie. Innymi słowy mówimy, że złożoność problemu jest równa złożoności najlepszego algorytmu, który go rozwiązuje.

Komputery to urządzenia bardzo nietypowe. Same jako takie nie mają sprecyzowanego, jasno zdefiniowanego zadania, do wykonywania którego zostały zaprojektowane. Zadania, które wykonuje komputer, mogą się w czasie zmieniać, a ich określenie odbywa się poprzez pisanie programów komputerowych. Owe programy formułuje się w specjalnym języku (Pascal, C/C++, Java, Python itp.), a następnie zleca komputerowi do wykonania.

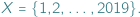Ustalmy zbiór np. Niech 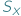oznacza zbiór funkcji odwracalnych z 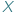w Funkcje z 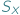można składać i odwracać, nie wychodząc poza 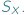W zbiorze 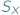istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru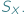

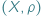Jednym z fundamentalnych pojęciem algebraicznych są pierścienie. Zostały one wprowadzone pod koniec XIX wieku z nadzieją na pomoc w udowodnieniu Wielkiego Twierdzenia Fermata. Jak wiadomo, zostało to uczynione dopiero w 1995 roku, więc przez długi czas nadzieja ta była płonna...

Pojęcie spójności przestrzeni metrycznej to uściślenie intuicji, że przestrzeń jest "w jednym kawałku".

Wyobraźmy sobie, że przyszło nam żeglować po jeziorze pod wiatr...

Geometria różniczkowa zajmuje się własnościami zbiorów opisanych przy użyciu funkcji różniczkowalnych (zwykle wielu zmiennych). Zbiory można opisywać m.in. przy użyciu układów równań lub za pomocą parametryzacji.

Przypuśćmy, że jest przestrzenią metryczną, czyli zbiorem 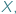w którym możemy mierzyć odległość między punktami tego zbioru. W przestrzeni metrycznej możemy zdefiniować pojęcie zbioru otwartego i domkniętego. Zacznijmy od przykładu podzbiorów płaszczyzny ze zwykłą, szkolną metryką euklidesową.

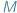Jeżeli każdej parze elementów danego zbioru (nazwijmy go ) przypiszemy odległość, zwaną także metryką (oznaczamy ją przez 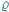), to powstanie przestrzeń metryczna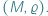

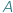Homeomorfizmy to przekształcenia zachowujące różne własności zbiorów (obiektów geometrycznych). Znaczy to, że pewne cechy obiektu są zachowywane przy "ściskaniu" lub "rozciąganiu", bez sklejania lub rozcinania, dziurawienia itp.

Ciągłość funkcji - na początku odwołamy się do intuicyjnego rozumienia tego pojęcia, by następnie je uściślić...

Zbieżność to jedno z najważniejszych pojęć analizy matematycznej, odnoszące się najczęściej do ciągów i funkcji (oraz rozmaitych obiektów matematycznych skonstruowanych przy ich użyciu, np. szeregów czy ciągów funkcyjnych). Tu zajmiemy się zbieżnością ciągów liczbowych.

Mając dane dwa zbiory i 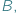relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru 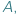a drugi ze zbioru 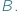Inaczej mówiąc, element ze zbioru 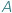i element ze zbioru 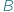mogą być w danej relacji lub w niej nie być.

Zbiór to najbardziej podstawowe pojęcie matematyki. Ze zbiorami mamy do czynienia właściwie we wszystkich dyscyplinach matematycznych. Choć każdy Czytelnik na pewno intuicyjnie rozumie słowo "zbiór" (np. jako kolekcję lub zestaw utworzony z pewnego rodzaju elementów), to pojęcie to nie ma formalnej definicji.

Biorąc dwa skończone zbiory, można na dwa sposoby sprawdzić, że mają tyle samo elementów. Albo policzyć elementy w każdym z nich, albo też ustawić w pary elementy pierwszego zbioru z elementami drugiego.

Teoria Gier (TG), traktowana jako dział matematyki, służy do wyjaśniania zachowań ludzi, zwierząt, przebiegu różnorodnych procesów w przyrodzie, ekonomii, medycynie, zachowania podmiotów w polityce, w sieciach społecznych, czyli - ogólniej - służy do opisu interakcji między różnego typu obiektami. Procesy te są na tyle złożone, że istniejące modele teoriogrowe nie przystają na ogół do obserwowanych sytuacji. Przykładem jest równowaga Nasha, która stanowi matematyczny opis stabilnego układu. Jednak w rzeczywistych sytuacjach ludzie nieczęsto grają strategiami tworzącymi taką równowagę.

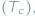Nadprzewodnictwo, jedno z najbardziej interesujących zjawisk fizycznych, zostało odkryte stosunkowo dawno - w roku 1911. Ciągle jednak fascynuje wielu fizyków, zarówno eksperymentatorów, jak i teoretyków. Jego istotą jest to, że w nadprzewodniku poniżej pewnej temperatury, nazywanej temperaturą krytyczną opór elektryczny oraz indukcja magnetyczna spadają do zera...

Czy zastanawialiście się kiedyś nad tym, czym jest inteligencja? Większość definicji zakłada posiadanie zdolności do rozumowania, uczenia się, adaptacji do zmieniającego się otoczenia. Najczęściej mówi się o inteligencji ludzi i zwierząt - organizmów mających mózg, a więc organ biologiczny. Czy inteligencja musi być jednak domeną jedynie istot, które uważamy obecnie za żywe? Wielu Czytelników słyszało zapewne również o inteligencji "sztucznej", określanej tak dlatego, że nie występuje ona w sposób naturalny w przyrodzie, ale w emergentny sposób pojawia się w maszynach i algorytmach tworzonych dzięki innej inteligencji, np. człowieka.

W 1994 roku Peter Shor, pracujący wówczas w Bell Labs w New Jersey, pokazał, jak przy użyciu hipotetycznego komputera kwantowego rozłożyć w czasie wielomianowym dowolną liczbę naturalną na czynniki pierwsze. W tamtym czasie algorytmy kwantowe dopiero raczkowały. To właśnie odkrycie Shora spowodowało wielki rozwój tej dziedziny. Społeczność informatyków zrozumiała, że gdyby udało się zbudować komputer kwantowy rozsądnej wielkości, to świat stałby się istotnie inny. Nie jest bowiem znany żaden algorytm dla problemu faktoryzacji, czyli rozkładu na dzielniki pierwsze, który działa w czasie wielomianowym na komputerze klasycznym. Co więcej, nawet nie znaleziono algorytmu losowego, który z dużym prawdopodobieństwem w zazwyczaj niedługim czasie faktoryzuje liczbę: nie jest po prostu znana zupełnie żadna rozsądna heurystyka...

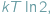"Informacja jest fizyczna" powiedział Rolf Landauer, fizyk, któremu zawdzięczamy zrozumienie faktu, że usunięcie 1 bitu informacji z pamięci komputera wiąże się z nieuniknionym wytworzeniem ciepła o wartości gdzie 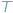jest temperaturą otoczenia, a 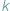stałą Boltzmanna. Był to wynik, który pokazał, że warto myśleć o fizycznych podstawach przetwarzanej przez nas informacji, aby zrozumieć ograniczenia i perspektywy dalszego rozwoju komputerów. Dziś wiemy, że materia na poziomie mikroskopowym opisywana jest przez prawa fizyki kwantowej...

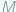W miejscowości jest fryzjer, nazwijmy go superfryzjerem, który strzyże tych i tylko tych mieszkańców miejscowości, którzy nie strzygą siebie samych. Czy superfryzjer strzyże siebie samego? Chwila namysłu pokazuje, że obie możliwości są wykluczone: nie może on strzyc siebie samego, bo strzyże tylko tych, którzy siebie sami nie strzygą; gdyby zaś sam się nie strzygł, to musiałby się strzyc, bo strzyże wszystkich tych, którzy sami się nie strzygą. A zatem, superfryzjer nie może istnieć! Pokażemy jak z powyższego faktu otrzymać różne twierdzenia matematyczne, odpowiednio definiując mieszkańców miejscowości 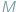oraz to, kto kogo strzyże.

Pogląd, iż ciała makroskopowe zbudowane są z drobnych składników jakimi są atomy i molekuły jest dzisiaj przyjmowany przez wszystkich fizyków za oczywisty. Stosując metody fizyki statystycznej możemy na podstawie praw rządzących ruchem tych składników wyprowadzić między innymi prawa termodynamiki, wyliczyć ciepło właściwe różnych substancji, ich podatność magnetyczną, opór elektryczny itp. Podstawy fizyki statystycznej zwanej dawniej teorią kinetyczno-molekularną zostały sformułowane w drugiej połowie XIX w. w pracach Clausiusa, Maxwella, Boltzmanna i Gibbsa...

W poprzednim numerze Delty opisaliśmy zmagania fizyków XIX wieku z problemem tzw. ruchów Browna. Przypomnijmy podstawowe fakty. W roku 1827 Robert Brown odkrył zygzakowate ruchy wykonywane przez drobne ziarenka zawieszone w cieczy. Ruchy te obserwowano dla wszystkich substancji, o ile zostały one tak rozdrobnione, że ziarenka miały średnicę co najwyżej kilku mikronów. Próby wyjaśnienia przyczyn ruchów Browna napotkały poważne trudności...

Opcje są kontraktami, które posiadaczowi dają prawo (ale nie obowiązek) zakupu (lub sprzedaży) określonego towaru w ustalonej chwili w przyszłości (termin realizacji) po ustalonej cenie (cena realizacji). Opcja jest więc umową, która jednej stronie (posiadaczowi) daje pewne prawa, które muszą być realizowane przez drugą stronę umowy (sprzedawcę opcji). Oczywiście, za uzyskane prawa posiadacz opcji musi zapłacić sprzedawcy określoną cenę.

Gotów jestem założyć się, Czytelniku, że wcześniej o niej nie słyszałeś. Tymczasem pod tą mało medialną nazwą kryje się metoda, dzięki której współczesne superkomputery pracują pełną parą, prowadząc skomplikowane symulacje. Łączy ona w sobie algorytmiczną efektywność z fizyczną intuicją, a bez wglądu w jej matematyczny sens, być może, nigdy byśmy jej nie poznali.

---

W dzisiejszym świecie cyfrowym mamy do czynienia z olbrzymią ilością danych, wielu Czytelników słyszało zapewne modne ostatnio hasło "Big Data". I trzeba sobie z tym radzić, a problemy mogą pojawiać się w nieoczekiwanych miejscach. Przyzwyczajeni jesteśmy do myślenia, że programy mają pewne dane na wejściu i te dane są tam na stałe, program może je w dowolnym momencie przeczytać. Czasami jednak nie do końca przystaje to do rzeczywistości...

Superkomputery pomagają w badaniach przyrody, projektowaniu urządzeń i leków. Czym są, jak działają, jakich używają procesorów, jak szybko liczą? Odpowiedzi na te pytania zilustrujemy przykładami kilku superkomputerów, w tym czterech najszybszych na świecie oraz największego w Polsce.

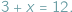Tak jak problemy praktyczne prowadzą do równań, tak równania prowadzą czasem do nowych rodzajów liczb. Ambitny kmieć z czasów Mieszka I, będący właścicielem trzech krów i marzący o nabyciu (lub zdobyciu) dodatkowych sztuk bydła tak, by stać się szanowanym posiadaczem tuzina krów, musiał niewątpliwie rozwiązywać zadanie matematyczne, które dziś zapisujemy równaniem Gdy zamienimy występujące tu liczby miejscami, otrzymamy równanie 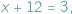które "nie da się rozwiązać": gołym okiem widać, że wśród liczb, za pomocą których zwykliśmy liczyć krowy (czyli liczb naturalnych), nie znajdzie się żadna, która by spełniała to równanie...

Od komputera oczekujemy przede wszystkim precyzji i dokładności. Program szukający wzorca w edytowanym tekście czy arkusz kalkulacyjny podsumowujący nasze miesięczne wydatki ma po prostu dać poprawny wynik. Wszelkie przejawy niedeterminizmu, losowości czy jakiejś niestabilności przywołują skojarzenia z działaniem niepożądanym. Zwykle to prawda: dobry program ma obliczyć, narysować czy wyanimować dokładnie to, czego od niego chcemy. Okazuje się jednak, że czasem losowość jest nie tylko wskazana, ale wręcz niezbędna.

Chyba w żadnym innym dziale fizyki nie uzyskano tak doniosłych wyników opartych na błędnym wyobrażeniu o naturze świata jak przy badaniu zjawisk cieplnych...

Dwieście lat temu główną osią sporu o naturę światła była kwestia, czy światło jest strumieniem cząstek, czy falą. Według dzisiejszego poglądu oba te wyobrażenia nie stoją ze sobą w sprzeczności i mieszczą się w ramach jednego wspólnego opisu dostarczanego przez elektrodynamikę kwantową. Na początku XIX wieku, nie łączono jeszcze światła ze zjawiskami elektrycznymi i magnetycznymi.

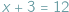Rozwiązywanie równań wymuszało poszerzenie zasobu liczb, jakimi się posługiwano. Równanie można było rozwiązać, posługując się najnaturalniejszymi liczbami, zwanymi zresztą naturalne, ale równanie 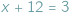wymagało rozszerzenia ich zasobu do liczb całkowitych. Wyjście poza obręb równań pierwszego stopnia pokazało, że do rozwiązania np. równania 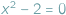nie wystarczą nie tylko liczby całkowite, ale nawet wszystkie liczby wymierne, czyli ułamki 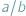zbudowane z liczb całkowitych. Aby uzyskać rozwiązanie, do liczb wymiernych trzeba dołączyć nowe liczby, a wśród nich liczbę niewymierną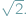

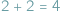Mechanika klasyczna opisuje dynamikę zarówno małych układów mechanicznych zbudowanych z ciężarków, dźwigni i sprężynek, jak i całego Układu Słonecznego, za pomocą kilku praw sformułowanych pierwszy raz przez Newtona pod koniec XVII wieku. Cały XVIII wiek to intensywny rozwój metod matematycznych inspirowanych mechaniką Newtona, pozwalających na coraz prostszy opis mechaniki i coraz efektywniejsze metody rozwiązywania równań opisujących układy mechaniczne. Sukces mechaniki klasycznej sprawił, że na początku XIX wieku niektórzy, jak cytowany przez G. Łukaszewicza Laplace, uwierzyli, że cały świat da się opisać prostymi, deterministycznymi prawami.

Co to znaczy udowodnić twierdzenie matematycznej Logicy dawno już odpowiedzieli na to pytanie, podając definicję dowodu formalnego jako ciągu zdań kończącego się dowodzonym twierdzeniem i o tej własności, że następne zdanie ciągu powstaje z poprzedniego w myśl prostych, ustalonych reguł.

Słyszy się często: "to pewne, jak ". Zdania matematyczne bywają podawane za wzór niewzruszonej i absolutnej prawdy. Pytanie, jakie zdania? Niewątpliwie pewniki, czyli aksjomaty ("przez dwa punkty przechodzi dokładnie jedna prosta") oraz twierdzenia, choćby tak łatwe, jak to zacytowane na początku.

Czym jest Bitcoin? Najkrótsza odpowiedź na to pytanie brzmi: kryptowalutą. Ale nie w takim sensie krypto-, jak w słowie kryptoreklama. Pierwszy człon tego terminu pochodzi od kryptologii, czyli nauki kojarzącej nam się głównie z szyframi i maszyną szyfrującą Enigma używaną przez Niemców podczas wojny. To właśnie twierdzenia i konstrukcje z tej dziedziny stoją za funkcjonowaniem i bezpieczeństwem Bitcoina.