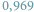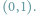W tym miesiącu będziemy prawdopodobnie świadkami najbardziej spektakularnego wydarzenia astronomicznego tego roku. Mało znana kometa okresowa 209P/LINEAR przejdzie przez peryhelium swojej orbity 6 maja w odległości  jednostki astronomicznej od Słońca.

Oto kolejna porcja wiadomości z odległych globów: prognoza pogody dla egzoplanety GJ 1214b. Praca synoptyka w układzie zawierającym ten glob, obiegający w 38 godzin wokół czerwonego karła Gliese 1214, a odległego od Układu Słonecznego o 40 lat świetlnych, jest najprawdopodobniej bardzo prosta, wygląda bowiem na to, że atmosfera planety jest zawsze pełna gęstych chmur.

Wenus, siostrzana planeta naszej Ziemi, jest bardzo wdzięcznym obiektem obserwacji astronomicznych, również tych amatorskich. W czerwcu 2012 roku byliśmy świadkami dość rzadkiego zjawiska astronomicznego, tzw. „przejścia”, czyli tranzytu Wenus na tle tarczy Słońca.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Tegoroczny Dzień Świętego Patryka może przejść do historii nauki. Jeżeli tylko potwierdzi się to, co ogłosił zespół badawczy eksperymentu BICEP2 [1], to odkrycie Higgsa 4 lipca 2012 roku (też łatwa do zapamiętania data) może się schować. Jeżeli się potwierdzi. Bo wynik został uzyskany w niezwykle zaawansowany sposób – łatwe odkrycia już dawno zostały zrobione. A w nawet najbardziej sumiennie przeprowadzonej analizie coś może umknąć uwagi zwiadowców.

Niektóre pierwiastki, takie jak fluor czy tlen – czyli w języku chemii te najbardziej elektroujemne – mają zdolność tworzenia specyficznego rodzaju wiązania jonowego, nazywanego wiązaniem wodorowym. Wiązania wodorowe są słabsze od wiązań kowalencyjnych i od zwykłych wiązań jonowych, a silniejsze niż oddziaływania van der Waalsa (choć siła tych ostatnich na ogół wzrasta wraz ze wzrostem liczby elektronów w cząsteczce)...

Nikt nie lubi sprawdzania swojej pracy, prawda? Udało nam się rozwiązać zadanie, bo wpadliśmy na pomysł i potrafiliśmy go zrealizować. Podobnie programista często potrafi napisać cały kod potrzebny do wykonania zadania, nim go choć raz uruchomi, by sprawdzić, czy program robi to, co było zamierzone. W taki „wir pracy” każdy z nas nieraz wpadł. W końcu właśnie w tym czujemy się najlepiej – w rozwiązywaniu problemów.

W tym kąciku proponuję zadanie polecane przez mojego korespondenta w Jekaterynburgu, mieście znanym również z turnieju Ural Sport Programming Championship, którego zeszłoroczną atrakcją był bezwzględny pojedynek pięciu najlepszych drużyn z Rosji z pięcioma najlepszymi drużynami z Chin. Popatrzmy na zadanie, którego nie udało się rozwiązać żadnej z nich!

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Kto by się spodziewał, że prawdziwe jest stwierdzenie: jeśli w sześcianie mieszczą się trzy jednakowe kulki, to zmieści się też czwarta tej samej wielkości!

Wyobraźmy sobie następującą grę. Mamy planszę o polach ponumerowanych od 0 do 100 i dwa pionki, stojące na początku na polu o numerze 0. Gracze wykonują ruchy na przemian. Gracz rzuca monetą i jeśli wypadnie reszka, to przesuwa swój pionek o 1 pole, a jeśli orzeł – o 5 pól. Wygrywa ten, kto pierwszy dojdzie do pola o numerze 100.

W pierwszej części artykułu szukaliśmy prawdopodobieństwa tego, że umierający człowiek będzie starszy od wszystkich aktualnie żyjących. Zadanie wykonaliśmy. Obliczyliśmy interesujące nas prawdopodobieństwo. Pozwólmy sobie teraz na kilka komentarzy i dygresji. Przypomnijmy najważniejszy wynik pomocniczy, który udowodniliśmy przed miesiącem.

3, 7, 31, 211, 2311, ... – jaki jest następny wyraz tego ciągu? Jakiś czas temu taka zagadka pojawiła się na jednej z polskich rozrywkowych stron internetowych. Niemal od razu w komentarzach pod nią rozpoczął się spór o poprawne, prawdziwe rozwiązanie. Czytelnik zapewne zechce podjąć wyzwanie samodzielnego odnalezienia następnego elementu ciągu i jego ogólnej reguły. Zatem zatrzymajmy się tu i pozwólmy sobie na chwilę namysłu; w dalszej części tekstu pojawi się rozwiązanie (autorowi niniejszego tekstu zajęło kilka dłuższych chwil znalezienie formuły).

W deltoidzie 7/2013 wykazaliśmy, że odcinek nie jest przeliczalny, posługując się tzw. metodą przekątniową Cantora. Tym razem udowodnimy ten sam fakt, wykorzystując pewną dwuosobową grę, której „planszą” jest zbiór 

Międzynarodowe konferencje Bridges odbywają się corocznie od 1998 roku w różnych krajach świata (w Europie, Ameryce i Azji). Dotyczą związków matematyki z różnymi dziedzinami sztuki (plastyka, muzyka, architektura, teatr, poezja, taniec). W czterodniowych obradach oraz wydarzeniach artystycznych uczestniczą naukowcy (głównie matematycy i informatycy), architekci, inżynierowie, nauczyciele, muzycy, tancerze, reżyserzy, rzeźbiarze, poeci i inni artyści oraz miłośnicy sztuki inspirowanej matematyką (lub na odwrót).

Nie jestem paleontologiem, interesują mnie odkrycia starożytnych genów. O problem pochodzenia współczesnych rdzennych Amerykanów (my, czytelnicy książek przygodowych, nazywamy ich po prostu „Indianami”) sprzeczają się badacze obu Ameryk do dziś. A ostatnio zwolennicy hipotezy „Pierwsi Clovis” dostali do ręki istotne dane pochodzące z badań genów. Może spory można zakończyć?