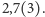Mała Delta
Znajomi moich znajomych
Wojtek leżał na podłodze i czytał właśnie książkę o grafach, którą wypożyczył z biblioteki. Alicja, jego młodsza siostra, która przeglądała w tym czasie portal społecznościowy, spytała nagle...

- Wojtek, czy uważasz, że jestem aspołeczna?
- Nie - uciął krótko.
- Mam 154 znajomych na NaszymPodwórku.
- To dużo.
- Krysia ma 210 znajomych, a Basia 245. Jednak nic nie przebije Ilony - najpopularniejszej dziewczyny w szkole - ma ona 510 znajomych.
Wojtek nie przejawiał zainteresowania rozmową ze swoją siostrą. Pochłonięty za to był lekturą.
- Obliczyłam właśnie, że moi znajomi mają średnio  znajomych.
znajomych.
- Jak to policzyłaś?
- No, normalnie - wzięłam średnią arytmetyczną.
- Zsumowałaś ręcznie 154 liczby?
- Nie bądź niemądry. Pomogłam sobie arkuszem kalkulacyjnym. Zresztą, to nie jest najważniejsze. Ważne jest to, że mam mniej znajomych na NaszymPodwórku niż średnio moi znajomi. Może powinnam się częściej udzielać w szkole? Od zawsze chciałam się zapisać na jakieś kółko zainteresowań.
- Uważam, że niepotrzebnie się przejmujesz. Myślę, że jest to sytuacja w pewnym sensie typowa.
- Przecież to matematycznie niemożliwe. Statystycznie połowa powinna mieć więcej znajomych niż średnio ich znajomi.
- No właśnie niekoniecznie. Weźmy tę twoją Ilonę. Ma ona 510 znajomych. Oznacza to, że podnosi ona średnią 510 osobom. Jeśli z kolei ktoś taki jak Tomek ma 10 znajomych, to obniża on średnią, ale tylko 10 osobom.
- No, nie wiem. Nie jestem do końca przekonana. Uważasz, że to jest jakaś reguła matematyczna? Można to udowodnić?
Wojtek zerwał się na równe nogi, chwycił za kartkę papieru i zaczął rysować.
- Być może możemy wykorzystać grafy!
- Grafy? - zaciekawiła się Alicja.
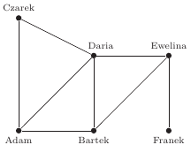
- Tak! Bo widzisz - znajomości na NaszymPodwórku można zaprezentować w postaci grafu. Te kropki, które teraz rysuję, to tak zwane wierzchołki. Każdy wierzchołek reprezentuje jednego użytkownika w serwisie. Teraz narysujemy krawędzie. Krawędzie to będą takie kreski między tymi wierzchołkami. Taka krawędź będzie oznaczała, że te dwie osoby mają się w znajomych.
- Daria ma najwięcej znajomych.
- Tak, ale…

- A Franek ma tylko jednego znajomego. To smutne.
- Nie o to chodzi! To tylko przykład. Policzmy lepiej, ile nasi bohaterowie mają znajomych.
- Adam ma trzech, Bartek też, Czarek ma dwóch. Daria ma czterech, Ewelina trzech, a Franek zna tylko Ewelinę. Biedny Franek.
- Czyli średnio mają 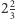 znajomych. Na przykładzie jest łatwo. Spróbujmy to teraz zrobić dla ogólnego grafu.
znajomych. Na przykładzie jest łatwo. Spróbujmy to teraz zrobić dla ogólnego grafu.
- Ale jak to zrobić? Przecież graf może wyglądać naprawdę przeróżnie!
- Każdy graf charakteryzują dwie liczby: liczba wierzchołków 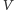 oraz liczba krawędzi
oraz liczba krawędzi 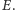 W naszym przykładzie
W naszym przykładzie 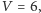 bo mamy 6 osób, a
bo mamy 6 osób, a 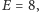 bo mamy 8 krawędzi łączących te osoby.
bo mamy 8 krawędzi łączących te osoby.
- Czy to wystarczy? Żeby obliczyć średnią arytmetyczną, potrzebujemy wiedzieć, ile każdy wierzchołek ma znajomych.

- Wystarczy, że będziemy wiedzieli, jaka jest suma wszystkich znajomych. Popatrzmy na jedną krawędź. Na przykład, między Czarkiem a Darią. Taka krawędź oznacza, że Czarek ma Darię w znajomych oraz Daria ma Czarka w znajomych. Zatem każda krawędź oznacza sumarycznie 2 osoby w znajomościach. Ponieważ mamy 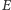 krawędzi, oznacza to, że nasi bohaterowie mają sumarycznie
krawędzi, oznacza to, że nasi bohaterowie mają sumarycznie 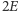 znajomych. Teraz wystarczy podzielić tę liczbę przez ilość osób, aby uzyskać średnią arytmetyczną.
znajomych. Teraz wystarczy podzielić tę liczbę przez ilość osób, aby uzyskać średnią arytmetyczną.
- 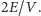 Faktycznie, jak podstawimy do wzoru dane z naszego przykładu, dostaniemy ten sam wynik, jaki obliczyliśmy bez tego wzoru! - ucieszyła się Alicja.
Faktycznie, jak podstawimy do wzoru dane z naszego przykładu, dostaniemy ten sam wynik, jaki obliczyliśmy bez tego wzoru! - ucieszyła się Alicja.
- Teraz będzie trudniej. Dla każdego wierzchołka musimy obliczyć, ile średnio znajomych mają jego znajomi. Następnie z tych wszystkich wartości chcielibyśmy obliczyć średnią.
- Wydaje się to trochę skomplikowane. Znowu będziemy patrzyli na krawędzie?
- Spróbujmy. Jeśli Czarek ma 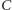 znajomych, a Daria
znajomych, a Daria 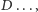 to
to 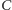 dodamy do znajomych znajomych Darii, a potem podzielimy przez
dodamy do znajomych znajomych Darii, a potem podzielimy przez 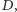 by obliczyć średnią. Tak samo będzie z Czarkiem. Do średniej liczby znajomych znajomych Czarka dodamy
by obliczyć średnią. Tak samo będzie z Czarkiem. Do średniej liczby znajomych znajomych Czarka dodamy 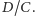
Wojtek zapisał na papierze 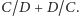
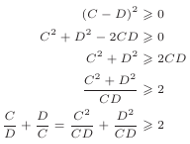
- To jest zawsze większe od dwóch! - zauważyła Alicja.
- Jest?
- Tak! Mieliśmy to w szkole. Zobacz! Pani zaczęła od tego, że kwadrat żadnej liczby nie może być ujemny. Jak się skorzysta ze wzoru skróconego mnożenia i to, co nie jest kwadratem, przeniesie na drugą stronę, to bez trudu wpada się na pomysł, że oprócz sprowadzenia do wspólnego mianownika, można robić też coś odwrotnego. I gotowe!
- Faktycznie. Ta suma będzie większa od dwóch… lub równa, ale tylko wtedy, gdy Czarek ma dokładnie tyle samo znajomych co Daria.
- Aha! Co musimy zrobić dalej?
- Musimy posumować po wszystkich krawędziach. Ponieważ mamy 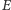 krawędzi, otrzymam coś większego od
krawędzi, otrzymam coś większego od 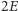 ...
...
- ... albo równego 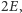 jeśli wszyscy użytkownicy mają dokładnie tyle samo znajomych - zauważyła Alicja.
jeśli wszyscy użytkownicy mają dokładnie tyle samo znajomych - zauważyła Alicja.
- I na koniec podzielić przez liczbę wierzchołków 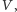 aby otrzymać średnią arytmetyczną.
aby otrzymać średnią arytmetyczną.
- Czyli ostatecznie otrzymaliśmy coś większego lub równego 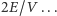 Czyli miałeś rację! Średnio nasi znajomi mają więcej znajomych niż my sami.
Czyli miałeś rację! Średnio nasi znajomi mają więcej znajomych niż my sami.
- No to, jak to już ustaliliśmy, mogę wrócić do mojej książki, a ty możesz wrócić do NaszegoPodwórka.
- Wiesz co? Chyba przejdę się do biblioteki poczytać o grafach. Mam w głowie tyle pytań. Na przykład, czy zawsze osoby, które mają mniej znajomych od średniej liczby znajomych jego znajomych, stanowią większość w grafie? A kto wie? Może przy okazji poznam kogoś ciekawego, kogo będę mogła dodać do znajomych na NaszymPodwórku.
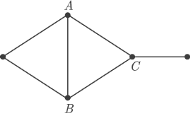
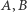 i
i 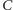 ma stopień równy
ma stopień równy 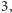 podczas gdy średnia stopni jego sąsiadów jest mniejsza niż
podczas gdy średnia stopni jego sąsiadów jest mniejsza niż 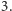 Niemniej jednak w tym grafie średnia stopni wynosi
Niemniej jednak w tym grafie średnia stopni wynosi 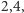 a średnia ze średnich stopni sąsiadów wynosi
a średnia ze średnich stopni sąsiadów wynosi