Drobiazgi
Cykle Hamiltona na wielościanach foremnych
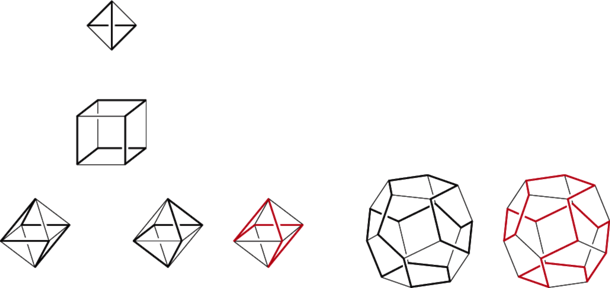
Zadanie 44 w książce 100 zadań Hugona Steinhausa dotyczy zamkniętych dróg po krawędziach wielościanu foremnego, które przechodzą dokładnie jeden raz przez każdy wierzchołek, czyli złożonych z krawędzi cykli Hamiltona. Chodzi o to, aby znaleźć wszystkie kształty takich cykli i policzyć, ile ich jest (z dokładnością do położenia) dla każdego wielościanu foremnego.
W oczywisty sposób stwierdzamy, że dla czworościanu i sześcianu otrzymujemy jeden kształt, trudniej zauważyć, że dla ośmiościanu jest ich trzy (w tym para lustrzana), a już całkiem trudno, że dla dwunastościanu jest tylko jedna lustrzana para. Te są tu narysowane. Polecamy natomiast Czytelnikom sprawdzenie, że dla dwudziestościanu jest 16 par lustrzanych i jeszcze jeden pojedynczy, a więc razem 33.