A nawet jeśli istnieje, to nie wiadomo, jak wiele kafelków trzeba użyć. Okazuje się, że zadanie ma elegancką interpretację w językach teorii grafów planarnych i sieci elektrycznych, która pomoże nam odpowiedzieć na te pytania.

Rys. 1

Zacznijmy od ogólniejszej sytuacji: dany jest prostokąt wykafelkowany kwadratami, na razie niekoniecznie różnymi - na przykład tak jak na rysunku 1. Kafelkowaniu przyporządkowujemy jego graf incydencji, czyli każdemu maksymalnemu poziomemu odcinkowi (być może złożonemu z boków kilku kwadratów) przypisujemy wierzchołek, a każdemu kafelkowi krawędź, w taki sposób, że krawędź odpowiadająca danemu kwadratowi łączy wierzchołki odpowiadające przeciwległym poziomym bokom tego kwadratu. Łatwo przekonać się, że powstały graf jest planarny, to znaczy można go narysować na płaszczyźnie tak, że nie ma przecinających się krawędzi.

Okazuje się, że konstrukcję tę można odwrócić, czyli przekształcać grafy planarne w kafelkowania. Żeby to zrobić, będziemy traktować taki graf jak obwód elektryczny. Przypomnimy najpierw podstawowe prawa dotyczące przepływu prądu w obwodzie.

Jeśli do dwóch punktów obwodu złożonego z oporników podłączymy baterię, na każdym oporniku wytworzy się różnica napięć i przepływ prądu zgodne z prawem Ohma:

gdzie 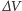to różnica potencjałów, 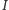- natężenie prądu, a 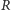- opór.

Załóżmy, że każda krawędź ma taki sam opór. Niech 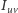oznacza natężenie prądu płynącego po krawędzi od wierzchołka do (a więc 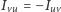). Bezpośrednio z prawa Ohma wnioskujemy, że dla dowolnego cyklu 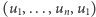w obwodzie suma natężeń prądów na tym cyklu jest równa zeru:

Z kolei prawo Kirchhoffa mówi, że w każdym wierzchołku suma natężeń prądów jest zerowa:

gdzie sumujemy po wszystkich wierzchołkach sąsiadujących z

Niech teraz 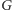będzie dowolnym grafem planarnym. Będziemy myśleć o 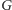jako o obwodzie elektrycznym, w którym każda krawędź ma jednostkowy opór. Wybierzmy w dowolny sposób dwa różne wierzchołki 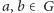położone na zewnętrznej ścianie grafu. Podłączmy do nich baterię generującą jednostkową różnicę potencjałów - możemy bez straty ogólności przyjąć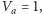 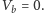W ten sposób w każdym wierzchołku otrzymamy pewną wartość potencjału elektrycznego 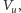a na każdej krawędzi 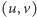przepływ prądu 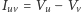(bo opór na krawędzi jest jednostkowy).

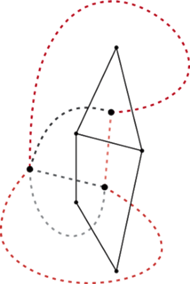
Rys. 2

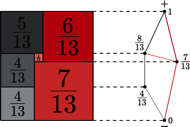
Kafelkowanie prostokąta odpowiadające grafowi 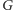konstruujemy w następujący sposób. Niech 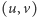będzie krawędzią, dla której 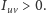Przyporządkowujemy jej kwadrat, którego dolny i górny brzeg znajdują się odpowiednio na wysokościach 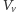i 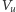(a więc długość jego boku jest równa 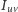). Aby otrzymać kafelkowanie, musimy jednak określić jeszcze, gdzie każdy kwadrat jest umieszczony w poziomie. Tu przychodzi nam z pomocą konstrukcja grafu dualnego. Dla grafu planarnego 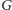graf dualny 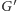jest określony następująco: wierzchołki 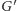odpowiadają ścianom 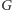(łącznie z zewnętrzną, nieograniczoną ścianą), przy czym dwa z nich są połączone krawędziami (Rys. 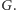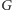2), jeśli odpowiadające im ściany sąsiadują w Czyli każdej krawędzi w odpowiada dualna krawędź 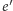w 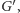a ściany w 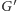odpowiadają wierzchołkom w 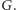Możemy narysować 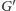tak: w każdej ścianie 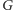zaznaczamy punkt, a następnie dla każdej krawędzi 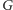rysujemy krawędź grafu dualnego łączącą punkty odpowiadające ścianom po obu jej stronach. Zwróćmy uwagę na to, że w ten sposób otrzymujemy nie tylko abstrakcyjną strukturę grafu dualnego, ale również pewien jego rysunek na płaszczyźnie. Na przykład wszystkie drzewa o 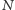krawędziach będą miały takie same abstrakcyjne grafy dualne (jeden wierzchołek z 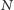pętlami), ale otrzymane reprezentacje na płaszczyźnie będą zależały od struktury (i wybranego rysunku!) drzewa.

Zauważmy teraz, że maksymalne pionowe odcinki w kafelkowaniu odpowiadają dokładnie ścianom w jego grafie incydencji. Ponadto z definicji maksymalne poziome odcinki odpowiadają wierzchołkom grafu incydencji. Ponieważ w grafie dualnym wierzchołki przechodzą na ściany, ściany na wierzchołki, a każda krawędź na krawędź, widzimy, że graf dualny jest niemal grafem incydencji kafelkowania obróconego o 90 stopni.

Należy jeszcze poradzić sobie z pewną niedogodnością: boki wyjściowego prostokąta odpowiadają ścianie zewnętrznej w grafie incydencji. Dodajmy więc do grafu 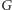specjalną krawędź między biegunami i 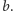W grafie dualnym 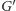bieguny baterii przykładamy między końcami krawędzi dualnej 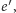a następnie usuwamy ją. Z powyższej obserwacji o obracaniu kafelkowania otrzymujemy przepis na współrzędne poziome kafelków: są one wyznaczone dokładnie przez natężenia prądów na krawędziach "poprawionego" grafu dualnego. Czytelnik Wnikliwy zapyta z pewnością, dlaczego taki wybór daje dobry układ kafelków, tzn. dlaczego nie ma w nim "dziur". Sprawdź, Czytelniku, że zapewnia to prawo Kirchhoffa!

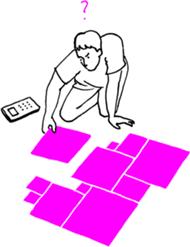
Każdemu grafowi planarnemu z wybranymi biegunami odpowiada zatem kafelkowanie prostokąta za pomocą kwadratów. Możemy przyjąć, że pionowy bok tego prostokąta ma długość 1. Jaka jest długość poziomego boku? To suma długości boków kafelków przylegających do niego, czyli suma natężeń prądów wypływających z bieguna baterii. Ponieważ 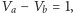to z prawa Ohma wynika, że suma ta jest równa odwrotności oporu zastępczego między 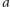i 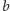w grafie 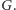Kafelkowanie kwadratu dostaniemy dokładnie wtedy, kiedy opór zastępczy będzie równy 1.

Wobec tego podaliśmy właśnie metodę znajdowania wszystkich możliwych kafelkowań kwadratu za pomocą parami różnych kafelków: należy znaleźć wszystkie grafy planarne o tej własności, że po przyłożeniu napięcia jednostkowego między pewnymi dwoma wierzchołkami opór zastępczy między nimi będzie równy 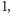a natężenia prądów na krawędziach będą niezerowe i parami różne. Korzystając z tej charakteryzacji, znaleziono, oczywiście używając komputera, liczne nowe przykłady kafelkowań kwadratów i innych prostokątów. Ich galerię można znaleźć na stronie http://www.squaring.net.

Na zakończenie wspomnijmy o jeszcze jednym nieoczekiwanym związku. Chcąc znaleźć wszystkie kafelkowania ustalonego prostokąta, wystarczy ograniczyć się do kafelkowań prostych, to znaczy takich, których nie da się podzielić pionowym odcinkiem na dwa rozłączne kafelkowania. Chwila zastanowienia pokazuje, że warunek ten jest równoważny 3-spójności grafu incydencji.

Pochodzące z kombinatoryki wielościanów twierdzenie Steinitza mówi, że 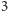-spójne grafy planarne to dokładnie szkielety wypukłych trójwymiarowych wielościanów. Czytelnik Wnikliwy może się więc zastanowić, jakiemu kafelkowaniu odpowiada jego ulubiony wielościan.