Najliczniejszy zbiór niezależny krawędzi (nk) to najliczniejszy podzbiór krawędzi, w którym żadne dwie nie są incydentne, czyli właśnie najliczniejsze skojarzenie w grafie.

---

Najmniejsze pokrycie krawędziowe (pk) to najmniej liczny podzbiór krawędzi, taki, że każdy wierzchołek jest incydentny z co najmniej jedną z nich.

---

Najliczniejszy zbiór niezależny wierzchołków (nw) to najliczniejszy podzbiór wierzchołków, w którym żadne dwa nie są sąsiednie, czyli żadne dwa nie są połączone krawędzią.

---

Najmniejsze pokrycie wierzchołkowe (pw) to najmniej liczny podzbiór wierzchołków, taki, że każda krawędź jest incydentna z co najmniej jednym z nich.

---

Jak łatwo zauważyć, powyższe definicje można również odnieść do zupełnie dowolnego grafu, a nie tylko do grafu dwudzielnego. Jednak w przypadku grafów dwudzielnych związki między podanymi pojęciami okażą się o wiele bardziej widoczne.

Oznaczmy przez  łączną liczbę wierzchołków w grafie. Odtąd założymy, że w grafie nie występują wierzchołki izolowane, czyli wierzchołki nieincydentne z żadną krawędzią. Wówczas zachodzą następujące równości, wiążące rozważane parametry w pary. Są to tzw. równości Gallaia. Są one prawdziwe w dowolnym grafie, jednak Czytelnikowi może być łatwiej je sobie wyobrazić w kontekście grafu dwudzielnego.

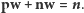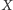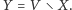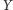 Niech  oznacza dowolne pokrycie wierzchołkowe w grafie. Rozważmy zbiór  Wówczas żadne dwa wierzchołki ze zbioru  nie mogą być połączone krawędzią, gdyż byłaby to krawędź niepokryta przez wierzchołki ze zbioru 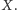 Stąd zbiór 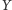 jest zbiorem niezależnym wierzchołków (patrz też rysunki powyżej). Przyjmując jako 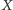 najmniejsze pokrycie wierzchołkowe, otrzymujemy nierówność

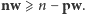
Podobnie widzimy, że jeśli 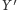 jest dowolnym zbiorem niezależnym wierzchołków, to 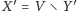 jest pokryciem wierzchołkowym w grafie. Stąd 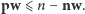 Z połączenia otrzymanych nierówności uzyskujemy żądaną równość.

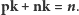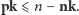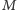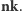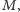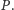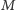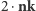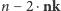 Znów wykażemy tak naprawdę dwie nierówności. Zacznijmy od nierówności  Niech  oznacza najliczniejsze skojarzenie w grafie, o liczności  Będziemy chcieli dołożyć pewne krawędzie do  tak aby otrzymać pokrycie krawędziowe  Skojarzenie  pokrywa  wierzchołków, do pokrycia pozostaje więc  wierzchołków. Każdy z nich jest incydentny z jakąś krawędzią – dodajmy zatem do 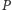 po jednej takiej krawędzi na każdy z tych wierzchołków (wcześniejsze rysunki stanowią tego dobrą ilustrację). Łącznie 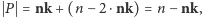 skąd

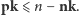
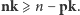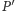Uzasadnimy teraz nierówność  Niech  oznacza najmniejsze pokrycie krawędziowe w grafie. Wówczas graf 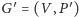 jest lasem, czyli grafem acyklicznym. Faktycznie, gdyby jakieś krawędzie w 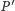  tworzyły cykl, to po usunięciu dowolnej z nich 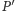 wciąż byłoby pokryciem krawędziowym, tyle że mniej licznym. Znanym faktem jest, że las o 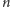  wierzchołkach i 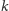  krawędziach składa się z   spójnych składowych. 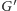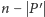Tak więc graf  składa się z   spójnych składowych, z których każda zawiera co najmniej jedną krawędź (inaczej 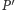 nie pokrywałoby wszystkich wierzchołków). Z każdej ze spójnych składowych 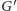 możemy teraz wybrać po jednej krawędzi. Otrzymany zbiór krawędzi na pewno będzie skojarzeniem, gdyż każda z krawędzi pochodzi z innej spójnej składowej. Stąd 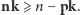 Obie nierówności dają łącznie równość, którą chcieliśmy uzyskać.

Dotychczasowe równości zachodziły w dowolnych grafach. Poniższa równość, znana także pod nazwą twierdzenia Königa, jest jedną z najlepiej znanych własności grafów dwudzielnych.

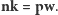 W tym przypadku nierówność 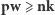 otrzymujemy za darmo – wszak aby pokryć krawędzie z najliczniejszego skojarzenia, trzeba na każdej z nich wybrać jakiś wierzchołek. Natomiast dużo ciekawsze jest uzasadnienie, że taka liczba wierzchołków zawsze wystarczy. Przeprowadzimy je, podając algorytm wyboru wierzchołków do pokrycia. Dowód przez algorytm – to w sumie ciekawe!

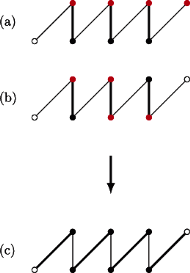
Algorytm działa na zasadzie wymuszeń. Do konstruowanego pokrycia możemy wziąć tylko 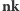 wierzchołków, możemy więc wybierać jedynie wierzchołki będące końcami krawędzi z pewnego najliczniejszego skojarzenia. Jeśli więc jakaś krawędź w grafie prowadzi do wierzchołka nieskojarzonego, to jej drugi koniec – będący z pewnością wierzchołkiem skojarzonym – musimy wybrać do pokrycia.

W ten sposób wybierzemy do pokrycia pewien zbiór wierzchołków skojarzonych. Niech 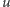 będzie jednym z tych wierzchołków i niech  będzie wierzchołkiem, który jest połączony z   krawędzią ze skojarzenia. Jeśli z   wychodzi jakaś krawędź do innego wierzchołka 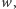 który jeszcze nie jest w pokryciu, to wiemy, że 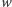 musimy umieścić w pokryciu. Dokładamy zatem 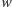 do pokrycia. W wyniku tego sąsiad wierzchołka 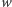 w skojarzeniu może spowodować kolejne wymuszenia itd.

Warto zastanowić się nad tym, jak może skończyć się ta sekwencja wymuszeń. Na pewno byłoby źle, gdyby w pokryciu znalazł się jakiś wierzchołek nieskojarzony, jak w przypadku (a), lub para wierzchołków skojarzonych, jak w przypadku (b). Przypadki te zostały zilustrowane na marginesie. W każdym z nich mamy do czynienia ze ścieżką, której końcami są wierzchołki nieskojarzone (puste kółka) i w której naprzemiennie występują krawędzie ze skojarzenia i spoza skojarzenia. Jest to tzw. ścieżka powiększająca; pojęcie to pojawiło się już w artykule Tomasza Idziaszka. Jeśli zamienić w takiej ścieżce krawędzie skojarzone na nieskojarzone i odwrotnie (sytuacja (c)), otrzyma się skojarzenie liczniejsze od obecnego, co nie jest możliwe, ponieważ zaczęliśmy od skojarzenia najliczniejszego.

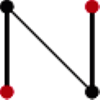
Wiemy zatem, że w wyniku wymuszeń z każdej pary wierzchołków skojarzonych wybierzemy do pokrycia wierzchołkowego co najwyżej jeden oraz że w pokryciu nie będzie żadnych innych wierzchołków. A co z pozostałymi krawędziami ze skojarzenia – tymi, z których nie został wybrany żaden wierzchołek? Czy możemy w każdej z nich po prostu wybrać do pokrycia po jednym, dowolnym wierzchołku? Niestety nie, co pokazuje rysunek na marginesie. Możemy jednak w każdej parze wybrać wierzchołek po tej samej stronie grafu dwudzielnego. Wówczas już otrzymamy poprawne pokrycie wierzchołkowe, czego nietrudne sprawdzenie pozostawiamy Czytelnikowi. To koniec dowodu twierdzenia Königa – nasz algorytm poprawnie konstruuje pokrycie wierzchołkowe o liczności

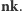
Z połączenia wszystkich równości, jakie otrzymaliśmy po drodze, uzyskujemy jeszcze jedną do kompletu: 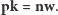 Oto pełny diagram: