Ukryte skojarzenia
Przedstawimy tu dwa zagadnienia, w których pojawia się problem znajdowania najliczniejszego skojarzenia w grafie dwudzielnym, jednak trochę ukryty.
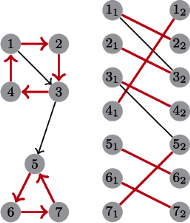
W pierwszym problemie mamy znaleźć tzw. pokrycie cyklowe grafu
skierowanego. Pokrycie cyklowe grafu
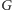 jest to zbiór cykli skierowanych
jest to zbiór cykli skierowanych
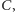 takich że każdy wierzchołek należy do dokładnie jednego cyklu
z
takich że każdy wierzchołek należy do dokładnie jednego cyklu
z
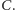 Chcielibyśmy szybko (tj. w czasie wielomianowym) odpowiadać
na pytanie, czy dany graf ma pokrycie cyklowe, a jeśli tak, chcielibyśmy
umieć wyznaczyć przykład takiego pokrycia.
Chcielibyśmy szybko (tj. w czasie wielomianowym) odpowiadać
na pytanie, czy dany graf ma pokrycie cyklowe, a jeśli tak, chcielibyśmy
umieć wyznaczyć przykład takiego pokrycia.
Rozwiązanie jest zaskakująco proste. Stwórzmy nowy graf
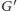 w następujący
sposób: każdy wierzchołek
w następujący
sposób: każdy wierzchołek
 oryginalnego grafu
oryginalnego grafu
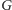 rozbijamy
w
rozbijamy
w
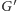 na dwa wierzchołki,
na dwa wierzchołki,
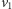 i
i
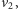 i jeśli w
i jeśli w
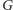 istniała
krawędź z
istniała
krawędź z
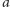 do
do
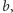 to w
to w
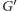 tworzymy krawędź
z
tworzymy krawędź
z
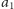 do
do
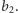
Okazuje się teraz, że jeśli najliczniejsze skojarzenie w
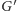 jest doskonałe
(każdy wierzchołek jest skojarzony), to graf
jest doskonałe
(każdy wierzchołek jest skojarzony), to graf
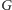 ma pokrycie cyklowe.
Formalne udowodnienie tego faktu jest dość proste: wystarczy pokazać
bijekcję ze zbioru pokryć cyklowych w
ma pokrycie cyklowe.
Formalne udowodnienie tego faktu jest dość proste: wystarczy pokazać
bijekcję ze zbioru pokryć cyklowych w
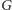 w zbiór skojarzeń
doskonałych w
w zbiór skojarzeń
doskonałych w
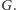 Szczegóły tego dowodu pozostawiam Czytelnikowi.
Rysunek na marginesie podpowiada, jak tej bijekcji szukać.
Szczegóły tego dowodu pozostawiam Czytelnikowi.
Rysunek na marginesie podpowiada, jak tej bijekcji szukać.
Kolejnym przykładem zastosowania skojarzeń w rozwiązywaniu problemów
jest wypełnianie kwadratów łacińskich. Kwadratem łacińskim nazywamy
macierz (tabelkę)
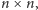 w której każdy wiersz i każda kolumna jest
permutacją ciągu
w której każdy wiersz i każda kolumna jest
permutacją ciągu
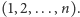 Przykłady kwadratów łacińskich
poniżej:
Przykłady kwadratów łacińskich
poniżej:
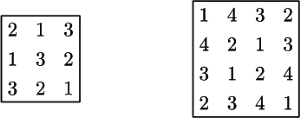
Rozważmy następujący problem: mamy kwadrat łaciński rozmiaru
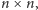 w którym pokazano nam tylko
w którym pokazano nam tylko
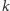 górnych wierszy (taki
nie do końca wypełniony kwadrat nazywamy prostokątem łacińskim rozmiaru
górnych wierszy (taki
nie do końca wypełniony kwadrat nazywamy prostokątem łacińskim rozmiaru
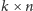 ). Chcemy zrekonstruować cały kwadrat łaciński, oczywiście
możliwie najszybciej.
). Chcemy zrekonstruować cały kwadrat łaciński, oczywiście
możliwie najszybciej.
Zamiast próbować rozwiązać ten problem w pełnej ogólności,
spróbujmy najpierw rozwiązać jego mniejszą część (informatycy tak lubią!).
Taką częścią problemu mogłoby być poprawne uzupełnienie wiersza
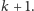 Jak to zrobić?
Jak to zrobić?
Konstruujemy graf dwudzielny
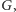 w którym wierzchołki z jednej grupy
będą reprezentować kolumny, natomiast wierzchołki z drugiej grupy
reprezentować będą liczby ze zbioru
w którym wierzchołki z jednej grupy
będą reprezentować kolumny, natomiast wierzchołki z drugiej grupy
reprezentować będą liczby ze zbioru
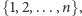 które będziemy
wpisywać do kolejnego wiersza. Jest już chyba jasne, że krawędź między
które będziemy
wpisywać do kolejnego wiersza. Jest już chyba jasne, że krawędź między
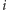 -tą kolumną a liczbą
-tą kolumną a liczbą
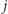 należy stworzyć wtedy i tylko wtedy, gdy
liczba
należy stworzyć wtedy i tylko wtedy, gdy
liczba
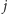 nie wystąpiła w
nie wystąpiła w
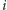 -tej kolumnie. W takim grafie szukamy
najliczniejszego skojarzenia. Jeśli jest ono doskonałe, wyznacza ono pewien
poprawny sposób wypełnienia wiersza
-tej kolumnie. W takim grafie szukamy
najliczniejszego skojarzenia. Jeśli jest ono doskonałe, wyznacza ono pewien
poprawny sposób wypełnienia wiersza
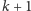 :
:
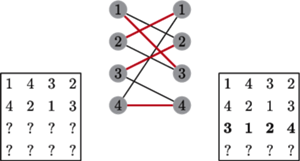
A co, jeśli w
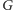 nie znajdziemy skojarzenia doskonałego? Okazuje się,
że taka sytuacja nigdy nie wystąpi! Zanim jednak udowodnimy ten fakt,
zauważmy, że właśnie uzyskaliśmy algorytm uzupełniający prostokąt do
kwadratu łacińskiego: wystarczy wypełniać kolejne wiersze poprzez
znajdowanie kolejnych skojarzeń doskonałych, a użyte krawędzie wyrzucać
z grafu. Po wyrzuceniu z grafu wszystkich krawędzi kwadrat łaciński będzie
uzupełniony.
nie znajdziemy skojarzenia doskonałego? Okazuje się,
że taka sytuacja nigdy nie wystąpi! Zanim jednak udowodnimy ten fakt,
zauważmy, że właśnie uzyskaliśmy algorytm uzupełniający prostokąt do
kwadratu łacińskiego: wystarczy wypełniać kolejne wiersze poprzez
znajdowanie kolejnych skojarzeń doskonałych, a użyte krawędzie wyrzucać
z grafu. Po wyrzuceniu z grafu wszystkich krawędzi kwadrat łaciński będzie
uzupełniony.
Nadszedł czas na dowód faktu, że w skonstruowanym zgodnie z powyższą
metodą grafie
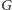 zawsze istnieje skojarzenie doskonałe. Zauważmy, że
graf
zawsze istnieje skojarzenie doskonałe. Zauważmy, że
graf
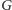 jest grafem regularnym, czyli stopnie wszystkich wierzchołków są
w nim takie same (są one równe
jest grafem regularnym, czyli stopnie wszystkich wierzchołków są
w nim takie same (są one równe
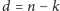 ). Okazuje się, że
w dwudzielnym grafie regularnym zawsze istnieje skojarzenie doskonałe.
). Okazuje się, że
w dwudzielnym grafie regularnym zawsze istnieje skojarzenie doskonałe.
Aby to wykazać, skorzystamy z twierdzenia Halla o małżeństwach. O
twierdzeniu Halla pisaliśmy już w artykułach Kaskady i swaty oraz
Skojarzenia w grafach kubicznych. Twierdzenie to głosi, że warunkiem
koniecznym i dostatecznym na istnienie doskonałego skojarzenia w grafie
dwudzielnym jest, aby każdy podzbiór wierzchołków z jednej grupy
(załóżmy, że jest on mocy
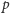 ) miał połączenie łącznie z co najmniej
) miał połączenie łącznie z co najmniej
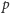 wierzchołkami z drugiej grupy (jest to tzw. warunek Halla).
Dowód naszego faktu wykorzystujący twierdzenie Halla jest bardzo prosty:
rozważmy dowolny podzbiór
wierzchołkami z drugiej grupy (jest to tzw. warunek Halla).
Dowód naszego faktu wykorzystujący twierdzenie Halla jest bardzo prosty:
rozważmy dowolny podzbiór
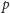 kolumn. Z każdego wierzchołka
odpowiadającego tym kolumnom wychodzi
kolumn. Z każdego wierzchołka
odpowiadającego tym kolumnom wychodzi
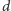 krawędzi, a więc łącznie
mamy
krawędzi, a więc łącznie
mamy
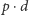 krawędzi. Gdyby warunek Halla dla rozważanego podzbioru
nie był prawdziwy, tzn. gdyby rozważany podzbiór był połączony krawędziami
z mniej niż
krawędzi. Gdyby warunek Halla dla rozważanego podzbioru
nie był prawdziwy, tzn. gdyby rozważany podzbiór był połączony krawędziami
z mniej niż
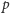 wierzchołkami z drugiej grupy, to na mocy zasady
szufladkowej Dirichleta do pewnego z tych wierzchołków musiałoby
prowadzić więcej niż
wierzchołkami z drugiej grupy, to na mocy zasady
szufladkowej Dirichleta do pewnego z tych wierzchołków musiałoby
prowadzić więcej niż
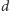 krawędzi. To jednak jest niemożliwe, gdyż
graf jest regularny. Stąd dla grafu
krawędzi. To jednak jest niemożliwe, gdyż
graf jest regularny. Stąd dla grafu
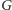 warunek Halla jest rzeczywiście
spełniony, więc
warunek Halla jest rzeczywiście
spełniony, więc
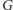 ma skojarzenie doskonałe.
ma skojarzenie doskonałe.
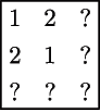
Warto jeszcze dodać, że gdybyśmy dostali do uzupełnienia prostokąt łaciński
wymiaru nie
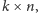 tylko
tylko
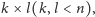 jego uzupełnienie do
kwadratu
jego uzupełnienie do
kwadratu
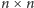 mogłoby okazać się niemożliwe. Obrazuje to podany
obok przykład.
mogłoby okazać się niemożliwe. Obrazuje to podany
obok przykład.