Cztery barwy wystarczą, czyli o kolorowaniu map
Pierwszy "dowód" twierdzenia o czterech barwach pojawił się w roku 1879. Przedstawił go Alfred Kempe, londyński prawnik. Był to zapewne najsłynniejszy "fałszywy dowód" w całej historii matematyki...
Gdy w październiku 1852 roku Francis Guthrie (były student Augustusa de Morgana) kolorował mapę Anglii, zauważył, że cztery kolory wystarczą, by każde dwa sąsiadujące hrabstwa różniły się barwą. Pomyślał:
Czy cztery barwy wystarczą do pokolorowania dowolnej, nawet najbardziej skomplikowanej mapy?
Pytaniem zainteresowało się zrazu kilku matematyków, w tym de Morgan i Sir William Rowan Hamilton, a później także Arthur Cayley, lecz pierwszy "dowód" pojawił się dopiero w roku 1879. Przedstawił go Alfred Kempe, londyński prawnik, który studiował z Cayleyem w Cambridge, a później przez wiele lat piastował stanowisko skarbnika Royal Society. Był to zapewne najsłynniejszy fałszywy dowód w całej historii matematyki, choć kryło się w nim także kilka dobrych pomysłów. A przebiegał on mniej więcej tak.
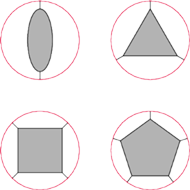
Rys. 1
Szkic rozumowania Kempego. Zakładamy, że wszystkie kraje na mapie poza jednym pokolorowaliśmy już czterema barwami, po czym pokazujemy, jak rozszerzyć to kolorowanie na ostatni, brakujący kraj. Każdą mapę zawierającą co najwyżej 4 kraje można oczywiście pokolorować czterema barwami zgodnie z regułami sąsiedztwa, zatem taka metoda pozwoliłaby rozszerzyć kolorowanie na 5, 6, 7... krajów, czyli na wszystkie mapy. Otóż łatwo wywnioskować ze wzoru wielościennego Eulera, że na każdej mapie jest kraj, który ma co najwyżej pięciu sąsiadów: dwukąt (kraj o dwóch bokach), trójkąt, kwadrat lub pięciokąt. Kempe przeanalizował kolejno każdy z tych przypadków (Rys. 1).
Jeśli mapa zawiera dwukąt lub trójkąt, ściągamy go do punktu. Mamy wtedy mniej krajów, potrafimy więc pokolorować je czterema barwami. Gdy przywrócimy oryginalną figurę, będzie ona otoczona co najwyżej trzema krajami. Pozostanie zatem wolny kolor, którym możemy pokolorować ów dwukąt lub trójkąt zgodnie z regułami.
Jeśli na mapie znajduje się kwadrat, popatrzmy - idąc tropem rozumowania Kempego - na dwa tylko kolory, powiedzmy, na czerwony kraj bezpośrednio nad kwadratem i zielony kraj bezpośrednio pod kwadratem i rozważmy następujące pytanie: czy czerwono-zielona część mapy nad kwadratem jest połączona z czerwono-zieloną częścią mapy pod kwadratem?
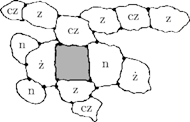
Rys. 2
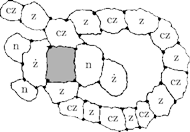
Rys. 3
Jeśli NIE (Rys. 2), to nad kwadratem możemy zamienić kolory czerwony i zielony (czerwone kraje stają się zielone i odwrotnie), w wyniku czego kraje leżące bezpośrednio nad i bezpośrednio pod kwadratem będą oba zielone - a wtedy możemy kwadrat pomalować na czerwono.
Jeśli jednak TAK (Rys. 3), to zamiana kolorów w niczym nie pomoże - kwadrat będzie wciąż otoczony czterema barwami. W takim przypadku popatrzmy na niebieski kraj leżący bezpośrednio na prawo i żółty kraj leżący bezpośrednio na lewo od kwadratu. Niebieskie i żółte terytoria po prawej są teraz oddzielone od takich samych terytoriów po lewej, gdyż rozdziela je pierścień czerwono-zielony. Możemy zatem po prawej stronie zamienić niebieski z żółtym bez szkody dla strony lewej, a następnie pokolorować kwadrat na niebiesko.
Wreszcie gdy mamy do czynienia z pięciokątem, Kempe proponuje podobne rozumowanie, wymagające jednak tym razem dwukrotnej zamiany kolorów, w wyniku której pięciokąt okaże się otoczony tylko trzema barwami, a czwarta zostanie dla niego. Tak kończy się dowód twierdzenia o czterech barwach.
Przez 11 lat rozumowanie Kempego było powszechnie akceptowane, m.in. przez Cayleya, więc bomba podrzucona przez Percy'ego Heawooda w 1890 roku wywołała nie lada efekt. Heawood wskazał na fundamentalny błąd w pracy Kempego, wykazując, że nie zawsze można wykonać dwukrotną zamianę kolorów w przypadku pięciokąta. Udało mu się jednak uratować część rozumowania, wystarczającą do udowodnienia, że każdą mapę można pokolorować pięcioma barwami - wynik wciąż jeszcze imponujący.
Heawood próbował również uogólnić problem kolorowania na inne powierzchnie. Rzut stereograficzny sfery na płaszczyznę pozwala zauważyć, że kolorowanie map na sferze jest tym samym, co kolorowanie map na płaszczyźnie, ale jak wygląda sprawa z kolorowaniem map na obwarzanku, czyli torusie? Tu magiczną okazała się liczba 7. Torusowa wersja wzoru wielościennego Eulera prowadzi do wniosku, że siedem barw wystarczy do pokolorowania dowolnej mapy na torusie, a jednocześnie Heawood podał przykład mapy, dla której konieczne jest użycie właśnie tylu kolorów.
Jeśli dopuścimy dziury w powierzchni (takie jak w preclu), to liczba niezbędnych barw wzrośnie. Jak udowodnił Heawood, do pokolorowania każdej mapy na obwarzanku z 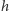 dziurami (gdy
dziurami (gdy 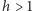 ) potrzeba
) potrzeba 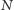 barw, przy czym
barw, przy czym
![1√ =[(7+1+48h)], N 2](/math/temat/matematyka/teoria_grafow/2011/05/16/Cztery_barwy_wystarcza/4x-d588f0b457b75b5cbf6c3499e7734b5a689b1ee4-dm-33,33,33-FF,FF,FF.gif)
gdzie ![[x]](/math/temat/matematyka/teoria_grafow/2011/05/16/Cztery_barwy_wystarcza/5x-d588f0b457b75b5cbf6c3499e7734b5a689b1ee4-im-33,33,33-FF,FF,FF.gif) oznacza część całkowitą liczby
oznacza część całkowitą liczby 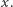 Heawoodowi nie udało się pokazać, że dla każdej powierzchni tego typu istnieje mapa, której nie można pokolorować mniejszą liczbą barw - ale to zajęło następne 78 lat. Okazało się, że dowód tej hipotezy Heawooda wymaga rozpatrzenia 12 zupełnie odmiennych przypadków.
Heawoodowi nie udało się pokazać, że dla każdej powierzchni tego typu istnieje mapa, której nie można pokolorować mniejszą liczbą barw - ale to zajęło następne 78 lat. Okazało się, że dowód tej hipotezy Heawooda wymaga rozpatrzenia 12 zupełnie odmiennych przypadków.
Do 1967 roku niemiecki matematyk Gerhard Ringel i jego amerykański kolega Ted Youngs rozstrzygnęli większość z nich. Korzystając z rocznego urlopu, Ringel pojechał do Kalifornii i po kilku miesiącach wspólnej pracy z Youngsem uzupełnili dowód o brakujące przypadki.
Tymczasem praca nad problemem czterech barw dawała efekty dość mierne. Choć trudno było naprawić błąd Kempego, można było jednak wydobyć z jego artykułu dwa pomysły, które miały okazać się przydatne w ostatecznym rozwiązaniu.
Pierwszy z nich to pojęcie nieuniknionego zbioru konfiguracji. Jak stwierdziliśmy wyżej, każda mapa zawiera figurę, która jest co najwyżej pięciokątem, zatem wymienione przy tej okazji konfiguracje (dwukąt, trójkąt, kwadrat, pięciokąt) stanowią przykład nieuniknionego zbioru: w każdej mapie jedna z nich musi wystąpić, nie można ich uniknąć. Z pierwszymi trzema umiemy sobie poradzić, trudność sprawia jedynie pięciokąt - spróbujmy więc zastąpić go czymś innym. Można wykazać, że każda mapa niezawierająca dwukąta, trójkąta ani kwadratu, zawiera nie tylko pięciokąt, ale również albo dwa sąsiadujące pięciokąty, albo pięciokąt sąsiadujący z sześciokątem. Mamy zatem nowy nieunikniony zbiór: dwukąt, trójkąt, kwadrat, dwa sąsiadujące pięciokąty, pięciokąt sąsiadujący z sześciokątem.
Widzieliśmy też, że dwukąt, trójkąt lub kwadrat jest konfiguracją redukowalną, co oznacza, że każde kolorowanie pozostałej części mapy czterema barwami można rozszerzyć tak, by objęło ono i tę konfigurację - czego nie umiemy zrobić z pięciokątem.
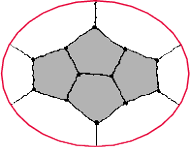
Rys. 4
Jednak w 1913 roku amerykański matematyk George Birkhoff wykazał, że redukowalna jest także konfiguracja pokazana na rysunku 4 - co otworzyło drogę do odkrycia tysięcy dalszych redukowalnych konfiguracji.
Widać zatem, że w celu udowodnienia, że cztery barwy wystarczą do pokolorowania każdej mapy, należy znaleźć nieunikniony zbiór konfiguracji redukowalnych, a więc taki zbiór konfiguracji, że każda mapa zawiera co najmniej jedną z nich - i ta, którą zawiera, jest redukowalna.
Przez pierwsze dwie trzecie XX wieku poszukiwano albo nieuniknionych zbiorów konfiguracji, albo konfiguracji redukowalnych. Pierwszym, który połączył te dwa pojęcia, był niemiecki matematyk Herman Heesch. Spędził on 40 lat na poszukiwaniach właśnie nieuniknionego zbioru redukowalnych konfiguracji. Wreszcie w 1976 roku pomysł Heescha został zrealizowany przez dwóch matematyków z Uniwersytetu stanu Illinois, Kennetha Apple'a i Wolfganga Hakena, wspomaganych w sprawach komputerowych przez studenta Johna Kocha. Po czterech latach poszukiwań z użyciem najpotężniejszych komputerów owego czasu znaleźli oni nieunikniony zbiór 1936 redukowalnych konfiguracji; po pewnym czasie udało im się go zmniejszyć do 1482 redukowalnych konfiguracji, a uzyskane rozwiązanie opublikowali w 1977 roku
Dowód wspomagany obliczeniami komputerowymi budził wówczas dużą podejrzliwość i rodził wiele filozoficznych pytań. Czy można uznać za poprawny dowód, którego nie możemy sprawdzić ręcznie, nawet jeśli udział komputera sprowadzał się do rutynowego zweryfikowania przypadków? Ale czy rzeczywiście powinniśmy pokładać wiarę w ręczny, ale niezmiernie długi dowód, powiedzmy, twierdzenia Feita-Thompsona o grupach rozwiązalnych, albo w dowód Wilesa dla Wielkiego Twierdzenia Fermata, gdzie możliwość ludzkiego błędu jest ogromna?
W latach 90. XX wieku czterech matematyków: Neil Robertson, Dan Sanders, Paul Seymour i Robin Thomas, przedstawiło bardziej strukturalny dowód twierdzenia o czterech barwach. Zastosowali oni podobne komputerowo wspomagane podejście co Apple i Haken, ale objęło ono tylko 600 redukowalnych konfiguracji, które można sprawdzić na laptopie w ciągu kilku godzin. Większość matematyków chętnie przyjmuje ten dowód, nawet jeśli mieli wątpliwości wobec dowodu Apple'a-Hakena. Nie mamy jednak, jak dotąd, żadnego dowodu, który obywałby się całkowicie bez komputera.
Tłumaczył Wiktor Bartol