Skojarzenia w grafach kubicznych
Skojarzenia to bardzo popularny temat. Pojawiają się w różnych miejscach zarówno w informatyce, jak i w matematyce dyskretnej.
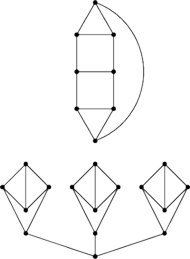
Dwa grafy kubiczne.
Definicja. W grafie nieskierowanym
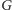 zbiór krawędzi
zbiór krawędzi
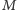 nazywamy skojarzeniem, jeśli żadne dwie krawędzie z
nazywamy skojarzeniem, jeśli żadne dwie krawędzie z
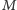 nie mają
wspólnego końca.
nie mają
wspólnego końca.
W tym artykule zajmiemy się skojarzeniami w grafach kubicznych. Graf
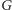 nazwiemy kubicznym, jeśli każdy wierzchołek
nazwiemy kubicznym, jeśli każdy wierzchołek
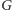 ma stopień
dokładnie
ma stopień
dokładnie
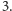
Mając dany graf
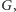 przez
przez
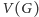 i
i
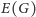 będziemy
oznaczać odpowiednio zbiór wierzchołków i krawędzi
będziemy
oznaczać odpowiednio zbiór wierzchołków i krawędzi
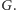 Ponadto
oznaczmy
Ponadto
oznaczmy
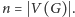 Dla wierzchołka
Dla wierzchołka
 przez
przez
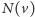 będziemy oznaczać zbiór sąsiadów
będziemy oznaczać zbiór sąsiadów
 ; tę notację rozszerzymy na
podzbiory wierzchołków:
; tę notację rozszerzymy na
podzbiory wierzchołków:
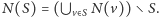 Skojarzenie
Skojarzenie
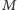 w grafie
w grafie
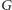 nazwiemy doskonałym, jeśli ma ono rozmiar
dokładnie
nazwiemy doskonałym, jeśli ma ono rozmiar
dokładnie
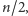 czyli każdy wierzchołek
czyli każdy wierzchołek
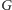 jest końcem
jakiejś krawędzi skojarzenia. Na rysunku pokazane są dwa grafy kubiczne:
pierwszy z nich ma doskonałe skojarzenie, a drugi nie ma. Czy łatwo jest
odróżnić grafy kubiczne z doskonałym skojarzeniem od tych, które takiego
nie mają?
jest końcem
jakiejś krawędzi skojarzenia. Na rysunku pokazane są dwa grafy kubiczne:
pierwszy z nich ma doskonałe skojarzenie, a drugi nie ma. Czy łatwo jest
odróżnić grafy kubiczne z doskonałym skojarzeniem od tych, które takiego
nie mają?
By odpowiedzieć na to pytanie, przypomnijmy sobie wpierw twierdzenie
Halla. Mamy graf dwudzielny
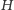 – dwudzielny, to znaczy, że zbiór
wierzchołków
– dwudzielny, to znaczy, że zbiór
wierzchołków
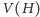 można podzielić na takie dwie części
można podzielić na takie dwie części
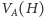 i
i
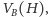 że wszystkie krawędzie
że wszystkie krawędzie
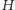 łączą
łączą
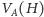 z
z
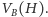 Interesuje nas to, czy w tym grafie istnieje
skojarzenie rozmiaru
Interesuje nas to, czy w tym grafie istnieje
skojarzenie rozmiaru
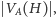 czyli takie, że wszystkie wierzchołki ze
zbioru
czyli takie, że wszystkie wierzchołki ze
zbioru
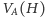 są skojarzone (każdy jest końcem pewnej krawędzi
skojarzenia). Jeśli istnieje taki zbiór
są skojarzone (każdy jest końcem pewnej krawędzi
skojarzenia). Jeśli istnieje taki zbiór
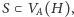 że
że
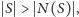 to ewidentnie takie skojarzenie nie istnieje: wierzchołki z
to ewidentnie takie skojarzenie nie istnieje: wierzchołki z
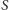 mają za mało
sąsiadów, by wszystkie były skojarzone. Twierdzenie Halla orzeka, że
powyższy warunek jest decydujący: jeśli dla każdego
mają za mało
sąsiadów, by wszystkie były skojarzone. Twierdzenie Halla orzeka, że
powyższy warunek jest decydujący: jeśli dla każdego
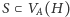 mamy
mamy
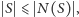 to w
to w
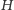 istnieje skojarzenie rozmiaru
istnieje skojarzenie rozmiaru
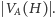
Twierdzenie Halla mówi o istnieniu dużych – kojarzących wszystkie
wierzchołki jednej części grafu – skojarzeń w grafach dwudzielnych. A jak to
jest dla dowolnych grafów? O tym mówi twierdzenie Tutte. Obierzmy dowolny
graf
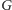 i zastanówmy się, co może przeszkadzać w tym, by
i zastanówmy się, co może przeszkadzać w tym, by
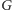 miał doskonałe skojarzenie. Weźmy dowolny zbiór wierzchołków
miał doskonałe skojarzenie. Weźmy dowolny zbiór wierzchołków
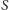 i wyrzućmy go z grafu, otrzymując graf
i wyrzućmy go z grafu, otrzymując graf
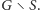 Spójrzmy na
pewną spójną składową
Spójrzmy na
pewną spójną składową
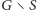 : jeśli ma ona nieparzyście wiele
wierzchołków, to w doskonałym skojarzeniu musiałaby istnieć krawędź
łącząca wierzchołek z tej spójnej składowej z wierzchołkiem z
: jeśli ma ona nieparzyście wiele
wierzchołków, to w doskonałym skojarzeniu musiałaby istnieć krawędź
łącząca wierzchołek z tej spójnej składowej z wierzchołkiem z
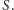 Wobec
tego nieparzystych spójnych składowych
Wobec
tego nieparzystych spójnych składowych
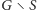 nie może być
więcej niż
nie może być
więcej niż
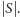 Twierdzenie Tutte mówi, że powyższy warunek
jest wystarczający: jeśli dla każdego zbioru wierzchołków
Twierdzenie Tutte mówi, że powyższy warunek
jest wystarczający: jeśli dla każdego zbioru wierzchołków
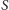 po wyrzuceniu
po wyrzuceniu
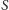 w
w
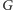 pozostaje nie więcej niż
pozostaje nie więcej niż
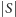 nieparzystych spójnych składowych, to w
nieparzystych spójnych składowych, to w
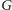 istnieje doskonałe
skojarzenie.
istnieje doskonałe
skojarzenie.
Wróćmy teraz do grafów kubicznych. Okazuje się, że tym, co może
przeszkadzać, by w grafie kubicznym istniało doskonałe skojarzenie, są mosty
(patrz np. dolny graf na rysunku). Krawędź
 jest mostem, jeśli
nie leży w żadnym cyklu, tj. po wyrzuceniu krawędzi
jest mostem, jeśli
nie leży w żadnym cyklu, tj. po wyrzuceniu krawędzi
 końce
końce
 leżą w różnych spójnych składowych. Spróbujemy wykorzystać
twierdzenie Tutte, by wykazać następujący:
leżą w różnych spójnych składowych. Spróbujemy wykorzystać
twierdzenie Tutte, by wykazać następujący:
Lemat. Jeśli graf kubiczny
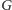 nie ma mostów, to ma doskonałe
skojarzenie.
nie ma mostów, to ma doskonałe
skojarzenie.
Dowód. Chcemy użyć twierdzenia Tutte, weźmy więc dowolny
podzbiór wierzchołków
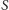 i zastanówmy się, ile może być
spójnych składowych o nieparzystej liczbie wierzchołków w
i zastanówmy się, ile może być
spójnych składowych o nieparzystej liczbie wierzchołków w
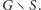 Weźmy taką spójną składową
Weźmy taką spójną składową
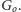 Zauważmy, iż łączny stopień
wierzchołków
Zauważmy, iż łączny stopień
wierzchołków
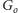 to
to
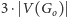 : jest to liczba nieparzysta,
czyli, na mocy lematu o uściskach dłoni, nieparzyście wiele krawędzi
łączy
: jest to liczba nieparzysta,
czyli, na mocy lematu o uściskach dłoni, nieparzyście wiele krawędzi
łączy
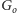 z resztą grafu. Jeśliby łączyła
z resztą grafu. Jeśliby łączyła
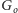 z resztą grafu tylko
jedna krawędź, to byłaby mostem: wobec tego istnieją co najmniej trzy
krawędzie łączące
z resztą grafu tylko
jedna krawędź, to byłaby mostem: wobec tego istnieją co najmniej trzy
krawędzie łączące
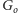 z resztą grafu. Skoro
z resztą grafu. Skoro
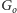 było spójną
składową
było spójną
składową
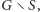 to te trzy krawędzie łączą
to te trzy krawędzie łączą
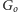 z
z
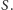 Z drugiej strony, łączny
stopień wierzchołków z
Z drugiej strony, łączny
stopień wierzchołków z
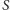 wynosi
wynosi
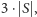 w
w
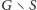 może być zatem co najwyżej
może być zatem co najwyżej
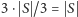 spójnych składowych
o nieparzystej liczbie wierzchołków, co kończy dowód lematu.
spójnych składowych
o nieparzystej liczbie wierzchołków, co kończy dowód lematu.
Wiemy już, że jeśli graf kubiczny nie ma mostów, to ma doskonałe
skojarzenie. Ale ile ma tych skojarzeń? Otóż do końca nie wiadomo.
W latach 70. ubiegłego wieku László Lovász i Michael Plummer postawili
hipotezę, że jest ich wykładniczo wiele: istnieje taka stała
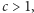 że
każdy graf kubiczny bez mostów ma co najmniej
że
każdy graf kubiczny bez mostów ma co najmniej
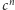 doskonałych
skojarzeń. Hipotezę tę dość szybko udowodnił Marc Voorhoeve dla grafów
kubicznych dwudzielnych. Bardzo niedawno Maria Chudnovsky oraz
Paul Seymour udowodnili hipotezę dla grafów planarnych: pokazali oni, że
graf kubiczny planarny bez mostów ma co najmniej
doskonałych
skojarzeń. Hipotezę tę dość szybko udowodnił Marc Voorhoeve dla grafów
kubicznych dwudzielnych. Bardzo niedawno Maria Chudnovsky oraz
Paul Seymour udowodnili hipotezę dla grafów planarnych: pokazali oni, że
graf kubiczny planarny bez mostów ma co najmniej
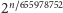 doskonałych skojarzeń. Z drugiej strony, Esperet, Král, Škoda i Škrekovski
pokazali, że w dowolnym grafie kubicznym bez mostów mamy co najmniej
doskonałych skojarzeń. Z drugiej strony, Esperet, Král, Škoda i Škrekovski
pokazali, że w dowolnym grafie kubicznym bez mostów mamy co najmniej
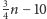 doskonałych skojarzeń i jest nadzieja na to, że niedługo
powstanie dowód, że istnieje ich co najmniej
doskonałych skojarzeń i jest nadzieja na to, że niedługo
powstanie dowód, że istnieje ich co najmniej
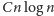 dla pewnej stałej
dla pewnej stałej
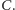 Jak widać, jeszcze długa droga pozostała do rozstrzygnięcia hipotezy
Lovásza–Plummera.
Jak widać, jeszcze długa droga pozostała do rozstrzygnięcia hipotezy
Lovásza–Plummera.