Rapsodia pajęcza
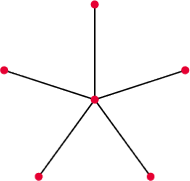
Rys. 1
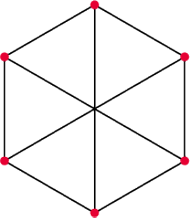
Rys. 2
Było piękne październikowe popołudnie. Przez wychodzące na zachód okno wpadały do pokoju ciepluśkie promienie słoneczka, wprowadzając miłą atmosferę błogiego lenistwa. Pod sufitem siedziały na ścianie dwa pająki, które dalekowzrocznie schroniły się już wewnątrz domostwa przed jesienno-zimowym chłodem. Imiona pająków są nieistotne w tej historii. Wspomnijmy może tylko, że dopiero czytane od końca znaczyły coś w języku polskim. Aby przezwyciężyć nudę, większy pająk zaproponował mniejszemu utkanie pajęczyn, ale żeby było zabawniej, narzucił dodatkowe warunki, że pajęczyny muszą mieć po sześć węzłów (węzeł w pajęczynie to miejsce, gdzie nić przyklejona jest do otoczenia) oraz nie może być w niej trzech węzłów, które tworzą trójkąt, czyli dla dowolnych trzech węzłów w pajęczynie muszą istnieć wśród nich dwa niepołączone nicią. Mniejszy pająk przystał chętnie na taką propozycję, szczególnie że już powoli zaczynał głodnieć i należało zacząć myśleć o polowaniu. Po utkaniu zaledwie pięciu nici (rys. 1) zorientował się, że już w żaden sposób nie może dodać kolejnej, aby nie utworzyć trójkąta. Jak złapać cokolwiek w tak rzadką sieć!? Spojrzał na pajęczynę większego pająka (rys. 2) i ze zdziwieniem stwierdził, że tamta złożona jest z dziewięciu nici. Całkiem porządna sieć! W oczekiwaniu na złapanie jakiejś zdobyczy, mniejszy pająk postanowił pomyśleć, gdzie popełnił błąd. . .
My też zastanówmy się, jak powinien postąpić mniejszy pająk, aby jego sieć była lepsza. Najpierw sformalizujmy sobie pojęcie pajęczyny. W naszym przypadku dobrym dla niej modelem matematycznym jest graf. Graf składa się z węzłów oraz krawędzi i możemy sobie go wyobrażać jako rysunek, na którym węzły są punktami, a krawędzie to krzywe, które łączą niektóre z węzłów tak, jak nici w pajęczynie łączą jej węzły. Przykłady grafów można znaleźć na rysunkach.
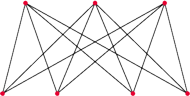
Rys. 3
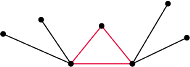
Rys. 4. Sąsiadujące węzły nie mogą mieć wspólnego sąsiada, gdyż wtedy mielibyśmy w naszym grafie trójkąt!
Problem naszych pająków to skonstruowanie
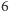 -węzłowego grafu
o możliwie dużej liczbie krawędzi niezawierającego trójkąta. Oczywiście,
nie będziemy się ograniczać do tak małej liczby węzłów i od razu zajmiemy się
tym problemem dla dowolnej liczby
-węzłowego grafu
o możliwie dużej liczbie krawędzi niezawierającego trójkąta. Oczywiście,
nie będziemy się ograniczać do tak małej liczby węzłów i od razu zajmiemy się
tym problemem dla dowolnej liczby
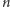 węzłów. Szukamy największej
możliwej liczby krawędzi w grafie o
węzłów. Szukamy największej
możliwej liczby krawędzi w grafie o
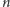 węzłach niezawierającym
trójkąta, czyli bez trzech węzłów połączonych krawędziami każdy
z każdym. Skonstruujmy sobie pewien graf
węzłach niezawierającym
trójkąta, czyli bez trzech węzłów połączonych krawędziami każdy
z każdym. Skonstruujmy sobie pewien graf
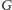 . Mamy do dyspozycji
. Mamy do dyspozycji
 węzłów. Podzielmy je na dwie części tak równo, jak to tylko
możliwe, tzn. jeśli
węzłów. Podzielmy je na dwie części tak równo, jak to tylko
możliwe, tzn. jeśli
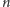 jest parzyste, to podzielimy węzły na dwie grupy
mające tyle samo
jest parzyste, to podzielimy węzły na dwie grupy
mające tyle samo
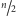 węzłów, a jeśli
węzłów, a jeśli
 jest nieparzyste, to
w jednej grupie będziemy mieli jeden węzeł więcej niż w drugiej –
grupy te będą miały liczności
jest nieparzyste, to
w jednej grupie będziemy mieli jeden węzeł więcej niż w drugiej –
grupy te będą miały liczności
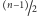 i
i
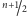 . Dwa węzły
w naszym grafie będą połączone krawędzią wtedy i tylko wtedy, gdy należą
do różnych grup. Przykładowy graf
. Dwa węzły
w naszym grafie będą połączone krawędzią wtedy i tylko wtedy, gdy należą
do różnych grup. Przykładowy graf
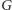 jest przedstawiony na
rysunku 3. Zauważmy, że nie znajdziemy w nim trójkąta, ale już
nie możemy dołożyć żadnej krawędzi bez stworzenia jakiegoś. A ile
graf
jest przedstawiony na
rysunku 3. Zauważmy, że nie znajdziemy w nim trójkąta, ale już
nie możemy dołożyć żadnej krawędzi bez stworzenia jakiegoś. A ile
graf
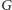 ma krawędzi? W przypadku
ma krawędzi? W przypadku
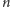 parzystego
parzystego
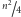 ,
a w przypadku przeciwnym
,
a w przypadku przeciwnym
 prawie tyle samo, a mianowicie jego
liczba krawędzi jest największą liczbą całkowitą nieprzekraczającą
prawie tyle samo, a mianowicie jego
liczba krawędzi jest największą liczbą całkowitą nieprzekraczającą
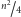 .
Zatem w obu przypadkach liczba krawędzi nie przekracza
.
Zatem w obu przypadkach liczba krawędzi nie przekracza
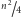 . Czy
. Czy
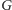 ma dużo krawędzi? Okazuje się, że graf bez trójkątów, mający
ma dużo krawędzi? Okazuje się, że graf bez trójkątów, mający
 węzłów, nie może mieć ich więcej! Można to wykazać, stosując
indukcję matematyczną.
węzłów, nie może mieć ich więcej! Można to wykazać, stosując
indukcję matematyczną.
Będzie to indukcja po
 liczbie węzłów. Dla małych wartości
liczbie węzłów. Dla małych wartości
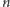 z łatwością sprawdzamy, że nasze twierdzenie jest prawdziwe. Pierwszy krok
indukcyjny mamy za sobą. Zabierzmy się za drugi. Weźmy dowolny
z łatwością sprawdzamy, że nasze twierdzenie jest prawdziwe. Pierwszy krok
indukcyjny mamy za sobą. Zabierzmy się za drugi. Weźmy dowolny
 -węzłowy graf niezawierający trójkątów. Taki graf musi zawierać
węzeł, z którego wychodzi mniej niż
-węzłowy graf niezawierający trójkątów. Taki graf musi zawierać
węzeł, z którego wychodzi mniej niż
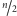 krawędzi. Rzeczywiście!
Weźmy dwa połączone krawędzią węzły. Nie mogą one oba być połączone
krawędzią z tym samym węzłem, gdyż wtedy tworzyłyby we trójkę zakazaną
konfigurację – trójkąt. Zatem łącznie z naszych dwóch węzłów może
wychodzić co najwyżej
krawędzi. Rzeczywiście!
Weźmy dwa połączone krawędzią węzły. Nie mogą one oba być połączone
krawędzią z tym samym węzłem, gdyż wtedy tworzyłyby we trójkę zakazaną
konfigurację – trójkąt. Zatem łącznie z naszych dwóch węzłów może
wychodzić co najwyżej
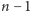 krawędzi (
krawędzi (
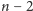 do pozostałych
węzłów oraz jedna łącząca je), ale to oznacza, że z któregoś z nich
wychodzi mniej niż
do pozostałych
węzłów oraz jedna łącząca je), ale to oznacza, że z któregoś z nich
wychodzi mniej niż
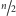 krawędzi, co chcieliśmy wykazać. Usuńmy ten
właśnie węzeł i wszystkie wychodzące z niego krawędzie. Otrzymany graf ma
krawędzi, co chcieliśmy wykazać. Usuńmy ten
właśnie węzeł i wszystkie wychodzące z niego krawędzie. Otrzymany graf ma
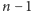 węzłów i nie zawiera trójkątów, bo się przecież żaden po
usunięciu węzła nie mógł pojawić, więc z założenia indukcyjnego zawiera
on co najwyżej
węzłów i nie zawiera trójkątów, bo się przecież żaden po
usunięciu węzła nie mógł pojawić, więc z założenia indukcyjnego zawiera
on co najwyżej
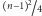 krawędzi. Nasz wyjściowy graf zawiera
wszystkie te krawędzie oraz krawędzie wychodzące z usuniętego węzła,
których jest nie więcej niż
krawędzi. Nasz wyjściowy graf zawiera
wszystkie te krawędzie oraz krawędzie wychodzące z usuniętego węzła,
których jest nie więcej niż
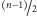 . Stąd nasz graf ma co najwyżej
. Stąd nasz graf ma co najwyżej
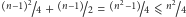 krawędzi, co było do wykazania. Dodatkowo
skonstruowany przez nas graf
krawędzi, co było do wykazania. Dodatkowo
skonstruowany przez nas graf
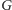 jest jedynym, który realizuje tę
największą liczbę krawędzi. Udowodnione przed chwilą twierdzenie nosi nazwę
twierdzenia Mantela.
jest jedynym, który realizuje tę
największą liczbę krawędzi. Udowodnione przed chwilą twierdzenie nosi nazwę
twierdzenia Mantela.

Rys. 5 Przykład grafu
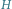 dla parametrów
dla parametrów
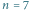 i
i
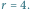
Gdy podstawimy
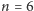 , widzimy, że większy pająk utkał najlepszą
możliwą sieć. A co z drugim pająkiem? On postąpił najgorzej jak
tylko można, gdyż, jak nietrudno wykazać,
, widzimy, że większy pająk utkał najlepszą
możliwą sieć. A co z drugim pająkiem? On postąpił najgorzej jak
tylko można, gdyż, jak nietrudno wykazać,
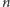 -węzłowy graf
niezawierający trójkąta o tej własności, że po dołożeniu dodatkowej
krawędzi trójkąt się pojawia, nie może mieć mniej niż
-węzłowy graf
niezawierający trójkąta o tej własności, że po dołożeniu dodatkowej
krawędzi trójkąt się pojawia, nie może mieć mniej niż
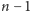 krawędzi.
krawędzi.
Czytelnik może spróbować skonstruować
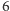 -węzłowy graf spełniający
nasze warunki mający jakąś pośrednią, między ekstremalnymi
-węzłowy graf spełniający
nasze warunki mający jakąś pośrednią, między ekstremalnymi
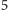 i
i
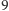 , liczbą krawędzi.
, liczbą krawędzi.
Po spałaszowaniu smakowitego komara mniejszy pająk zakrzyknął z tryumfem, że wie już, jak należy konstruować dobre sieci bez trójkątów. Wtedy większy pająk wysunął kolejną propozycję – utkania sieci, w której trójkąty mogą być, ale nie może być czterech węzłów, które są połączone nićmi każdy z każdym...
Hmmm... Pająki zadały nam nowe zadanie. Od razu zajmijmy się ogólniejszym
problemem. Zbiór
 węzłów w grafie, z których każdy z każdym
jest połączony krawędzią, nazwiemy
węzłów w grafie, z których każdy z każdym
jest połączony krawędzią, nazwiemy
 -kliką (czyli trójkąty to
-kliką (czyli trójkąty to
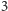 -kliki). Teraz nasz problem wygląda następująco: ile najwięcej krawędzi
może mieć
-kliki). Teraz nasz problem wygląda następująco: ile najwięcej krawędzi
może mieć
 -węzłowy graf niezawierający
-węzłowy graf niezawierający
 -kliki (
-kliki (
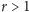 )?
Skonstruujemy sobie znowu graf. Nazwiemy go
)?
Skonstruujemy sobie znowu graf. Nazwiemy go
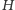 . Mamy do dyspozycji
. Mamy do dyspozycji
 węzłów. Podzielmy je na
węzłów. Podzielmy je na
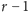 grup. Krawędzie w grafie
grup. Krawędzie w grafie
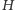 będą znowu łączyć węzły wtedy i tylko wtedy, gdy węzły te należą do
różnych grup. Nasz graf
będą znowu łączyć węzły wtedy i tylko wtedy, gdy węzły te należą do
różnych grup. Nasz graf
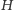 nie zawiera
nie zawiera
 -kliki – jeśli
wybierzemy dowolne
-kliki – jeśli
wybierzemy dowolne
 węzłów, to ponieważ grup jest tylko
węzłów, to ponieważ grup jest tylko
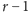 ,
co najmniej dwa węzły muszą należeć do tej samej grupy, a wtedy nie są one
połączone krawędzią. Zatem nasze dowolnie wybrane
,
co najmniej dwa węzły muszą należeć do tej samej grupy, a wtedy nie są one
połączone krawędzią. Zatem nasze dowolnie wybrane
 węzłów
nie tworzy
węzłów
nie tworzy
 -kliki w
-kliki w
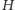 . Dołóżmy teraz do
. Dołóżmy teraz do
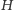 dowolną
krawędź. Wszystkie krawędzie pomiedzy różnymi grupami były już obecne
w
dowolną
krawędź. Wszystkie krawędzie pomiedzy różnymi grupami były już obecne
w
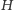 , więc nasza dołożona dopiero co krawędź musi łączyć wierzchołki
z jednej grupy. Wybierzmy z pozostałych
, więc nasza dołożona dopiero co krawędź musi łączyć wierzchołki
z jednej grupy. Wybierzmy z pozostałych
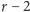 grup po jednym
węźle i dołóżmy je do tych dwóch węzłów. Mamy
grup po jednym
węźle i dołóżmy je do tych dwóch węzłów. Mamy
 węzłów,
z których każdy z każdym jest połaczony krawędzią, zatem do
węzłów,
z których każdy z każdym jest połaczony krawędzią, zatem do
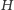 nie można już dołożyć żadnej krawędzi, aby cały czas spełniał on nasze
warunki.
nie można już dołożyć żadnej krawędzi, aby cały czas spełniał on nasze
warunki.
Czy skonstruowaliśmy tylko jeden graf
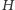 ? Ależ wyszła nam
cała rodzina grafów! Przecież kiedy dzieliliśmy
? Ależ wyszła nam
cała rodzina grafów! Przecież kiedy dzieliliśmy
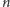 węzłów na
grupy, to mogliśmy uczynić to na wiele różnych sposobów (np. gdy
węzłów na
grupy, to mogliśmy uczynić to na wiele różnych sposobów (np. gdy
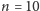 , a
, a
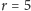 , to mamy możliwości
, to mamy możliwości
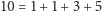 ,
,
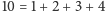 ,
,
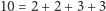 i kilka innych). Jak
powinniśmy podzielić nasze węzły na grupy, aby otrzymać największą liczbę
krawędzi w tak skonstruowanym grafie? Powinniśmy podzielić te
wierzchołki tak równo jak się da, tzn. tak, aby liczności poszczególnych grup
różniły się o co najwyżej
i kilka innych). Jak
powinniśmy podzielić nasze węzły na grupy, aby otrzymać największą liczbę
krawędzi w tak skonstruowanym grafie? Powinniśmy podzielić te
wierzchołki tak równo jak się da, tzn. tak, aby liczności poszczególnych grup
różniły się o co najwyżej
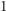 . Tę odmianę grafu
. Tę odmianę grafu
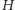 oznaczymy
przez
oznaczymy
przez
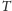 .
.
A może jest możliwość skonstruowania grafu w zupełnie inny sposób tak,
aby nie zawierał on
 -kliki i miał jeszcze więcej krawędzi niż
-kliki i miał jeszcze więcej krawędzi niż
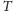 ?
Okazuje się, że nie! A graf
?
Okazuje się, że nie! A graf
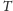 , nazywany grafem Turána od nazwiska
słynnego węgierskiego matematyka, jest jedynym grafem realizującym tę
największą (policz jaką!) liczbę krawędzi w
, nazywany grafem Turána od nazwiska
słynnego węgierskiego matematyka, jest jedynym grafem realizującym tę
największą (policz jaką!) liczbę krawędzi w
 -węzłowym grafie bez
-węzłowym grafie bez
 -klik. Czytelnika zainteresowanego wiekszą ilością szczegółów na
temat tego twierdzenia, zwanego – a jakże – twierdzeniem Turána, odsyłam do
książki Dowody z Księgi autorstwa Aignera i Zieglera, Wydawnictwo Naukowe
PWN, 2002.
-klik. Czytelnika zainteresowanego wiekszą ilością szczegółów na
temat tego twierdzenia, zwanego – a jakże – twierdzeniem Turána, odsyłam do
książki Dowody z Księgi autorstwa Aignera i Zieglera, Wydawnictwo Naukowe
PWN, 2002.
Skończyłem właśnie pisać arytkuł do ,,Delty”. Przeciągając się spojrzałem pod sufit i zobaczyłem, że mam tam całe mnóstwo pajęczyn o dziwnych, niecodziennych kształtach. Jedna nawet podobna była do grafu Turána... ,,Artykuł skończony – pora się wziąć za sprzątanie” – pomyślałem zdejmując pajęczyny.
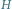 dla parametrów
dla parametrów
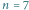 i
i